Large scale scattering using fast solvers based on neural operators

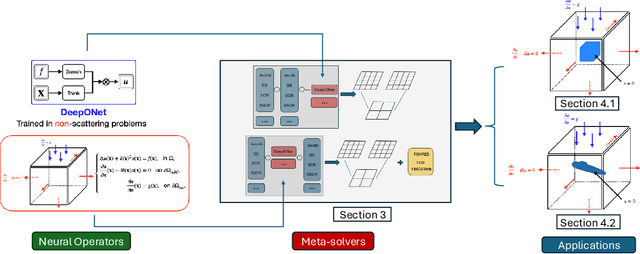
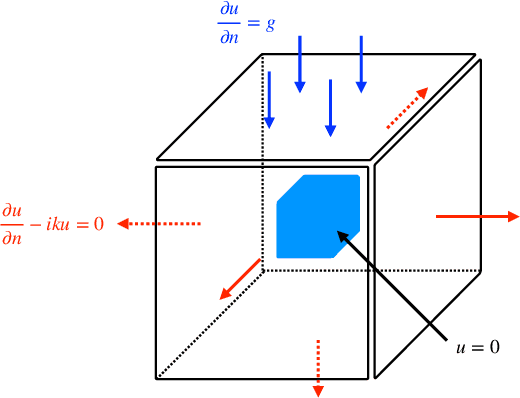
We extend a recently proposed machine-learning-based iterative solver, i.e. the hybrid iterative transferable solver (HINTS), to solve the scattering problem described by the Helmholtz equation in an exterior domain with a complex absorbing boundary condition. The HINTS method combines neural operators (NOs) with standard iterative solvers, e.g. Jacobi and Gauss-Seidel (GS), to achieve better performance by leveraging the spectral bias of neural networks. In HINTS, some iterations of the conventional iterative method are replaced by inferences of the pre-trained NO. In this work, we employ HINTS to solve the scattering problem for both 2D and 3D problems, where the standard iterative solver fails. We consider square and triangular scatterers of various sizes in 2D, and a cube and a model submarine in 3D. We explore and illustrate the extrapolation capability of HINTS in handling diverse geometries of the scatterer, which is achieved by training the NO on non-scattering scenarios and then deploying it in HINTS to solve scattering problems. The accurate results demonstrate that the NO in HINTS method remains effective without retraining or fine-tuning it whenever a new scatterer is given. Taken together, our results highlight the adaptability and versatility of the extended HINTS methodology in addressing diverse scattering problems.

Mechanical Characterization and Inverse Design of Stochastic Architected Metamaterials Using Neural Operators

Machine learning (ML) is emerging as a transformative tool for the design of architected materials, offering properties that far surpass those achievable through lab-based trial-and-error methods. However, a major challenge in current inverse design strategies is their reliance on extensive computational and/or experimental datasets, which becomes particularly problematic for designing micro-scale stochastic architected materials that exhibit nonlinear mechanical behaviors. Here, we introduce a new end-to-end scientific ML framework, leveraging deep neural operators (DeepONet), to directly learn the relationship between the complete microstructure and mechanical response of architected metamaterials from sparse but high-quality in situ experimental data. The approach facilitates the inverse design of structures tailored to specific nonlinear mechanical behaviors. Results obtained from spinodal microstructures, printed using two-photon lithography, reveal that the prediction error for mechanical responses is within a range of 5 - 10%. Our work underscores that by employing neural operators with advanced micro-mechanics experimental techniques, the design of complex micro-architected materials with desired properties becomes feasible, even in scenarios constrained by data scarcity. Our work marks a significant advancement in the field of materials-by-design, potentially heralding a new era in the discovery and development of next-generation metamaterials with unparalleled mechanical characteristics derived directly from experimental insights.

A Generative Modeling Framework for Inferring Families of Biomechanical Constitutive Laws in Data-Sparse Regimes

Quantifying biomechanical properties of the human vasculature could deepen our understanding of cardiovascular diseases. Standard nonlinear regression in constitutive modeling requires considerable high-quality data and an explicit form of the constitutive model as prior knowledge. By contrast, we propose a novel approach that combines generative deep learning with Bayesian inference to efficiently infer families of constitutive relationships in data-sparse regimes. Inspired by the concept of functional priors, we develop a generative adversarial network (GAN) that incorporates a neural operator as the generator and a fully-connected neural network as the discriminator. The generator takes a vector of noise conditioned on measurement data as input and yields the predicted constitutive relationship, which is scrutinized by the discriminator in the following step. We demonstrate that this framework can accurately estimate means and standard deviations of the constitutive relationships of the murine aorta using data collected either from model-generated synthetic data or ex vivo experiments for mice with genetic deficiencies. In addition, the framework learns priors of constitutive models without explicitly knowing their functional form, providing a new model-agnostic approach to learning hidden constitutive behaviors from data.

Recent Advances and Applications of Machine Learning in Experimental Solid Mechanics: A Review

For many decades, experimental solid mechanics has played a crucial role in characterizing and understanding the mechanical properties of natural and novel materials. Recent advances in machine learning (ML) provide new opportunities for the field, including experimental design, data analysis, uncertainty quantification, and inverse problems. As the number of papers published in recent years in this emerging field is exploding, it is timely to conduct a comprehensive and up-to-date review of recent ML applications in experimental solid mechanics. Here, we first provide an overview of common ML algorithms and terminologies that are pertinent to this review, with emphasis placed on physics-informed and physics-based ML methods. Then, we provide thorough coverage of recent ML applications in traditional and emerging areas of experimental mechanics, including fracture mechanics, biomechanics, nano- and micro-mechanics, architected materials, and 2D material. Finally, we highlight some current challenges of applying ML to multi-modality and multi-fidelity experimental datasets and propose several future research directions. This review aims to provide valuable insights into the use of ML methods as well as a variety of examples for researchers in solid mechanics to integrate into their experiments.

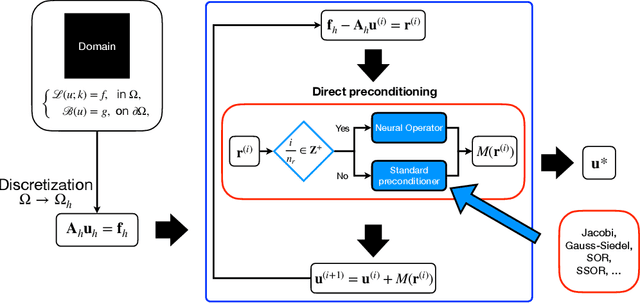
A Hybrid Iterative Numerical Transferable Solver (HINTS) for PDEs Based on Deep Operator Network and Relaxation Methods

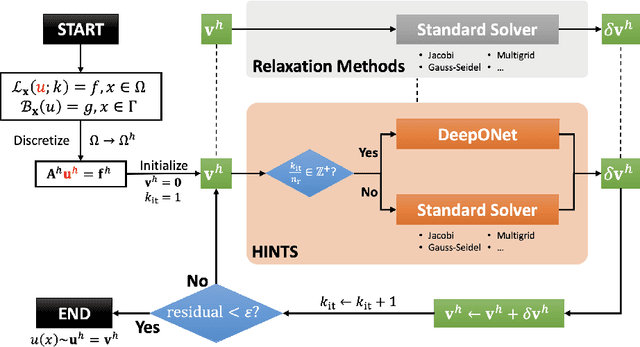
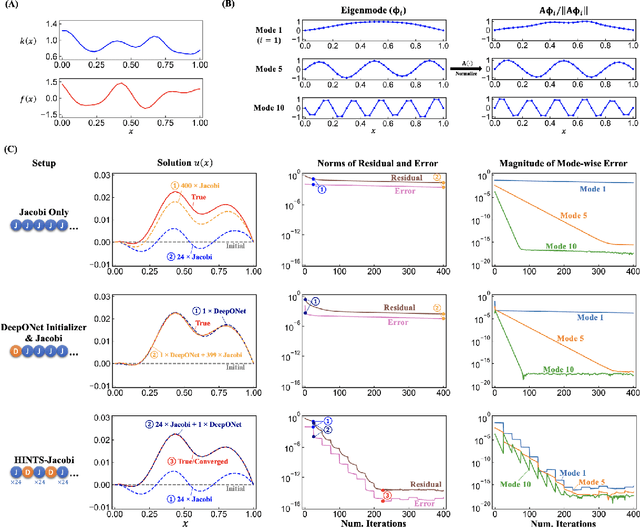
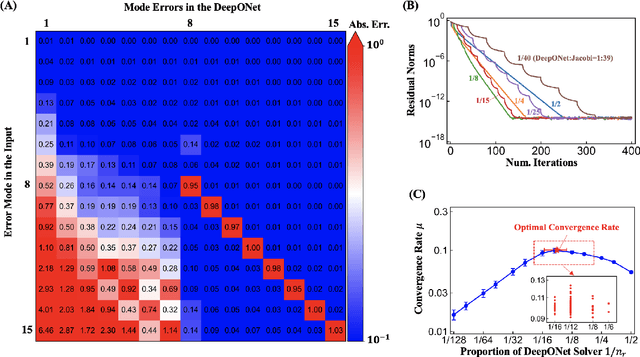
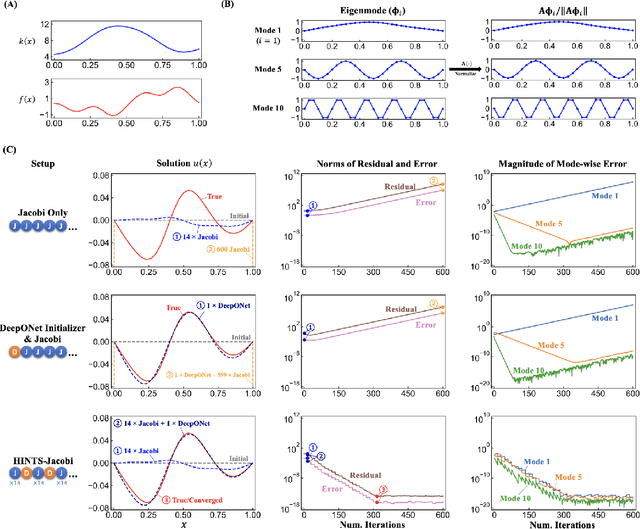
Iterative solvers of linear systems are a key component for the numerical solutions of partial differential equations (PDEs). While there have been intensive studies through past decades on classical methods such as Jacobi, Gauss-Seidel, conjugate gradient, multigrid methods and their more advanced variants, there is still a pressing need to develop faster, more robust and reliable solvers. Based on recent advances in scientific deep learning for operator regression, we propose HINTS, a hybrid, iterative, numerical, and transferable solver for differential equations. HINTS combines standard relaxation methods and the Deep Operator Network (DeepONet). Compared to standard numerical solvers, HINTS is capable of providing faster solutions for a wide class of differential equations, while preserving the accuracy close to machine zero. Through an eigenmode analysis, we find that the individual solvers in HINTS target distinct regions in the spectrum of eigenmodes, resulting in a uniform convergence rate and hence exceptional performance of the hybrid solver overall. Moreover, HINTS applies to equations in multidimensions, and is flexible with regards to computational domain and transferable to different discretizations.

G2Φnet: Relating Genotype and Biomechanical Phenotype of Tissues with Deep Learning

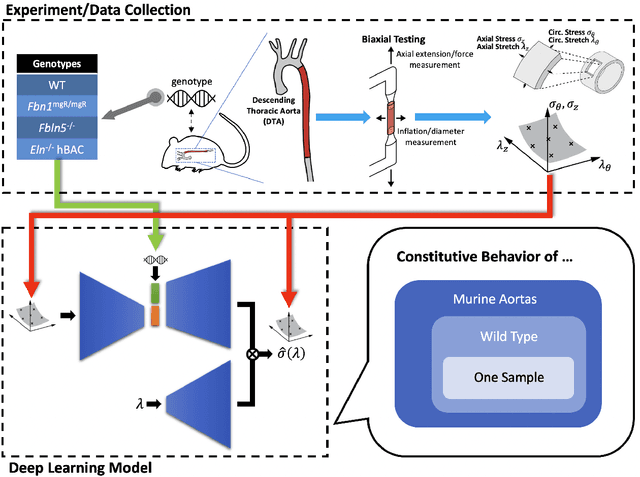
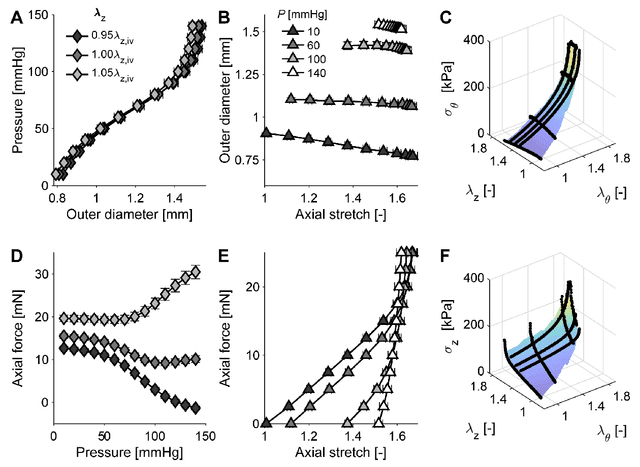
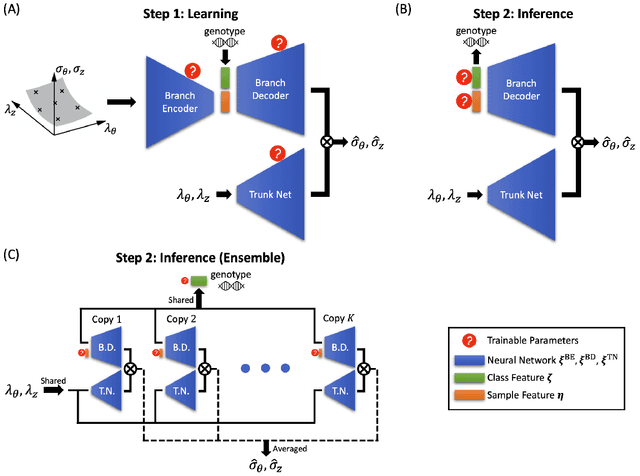
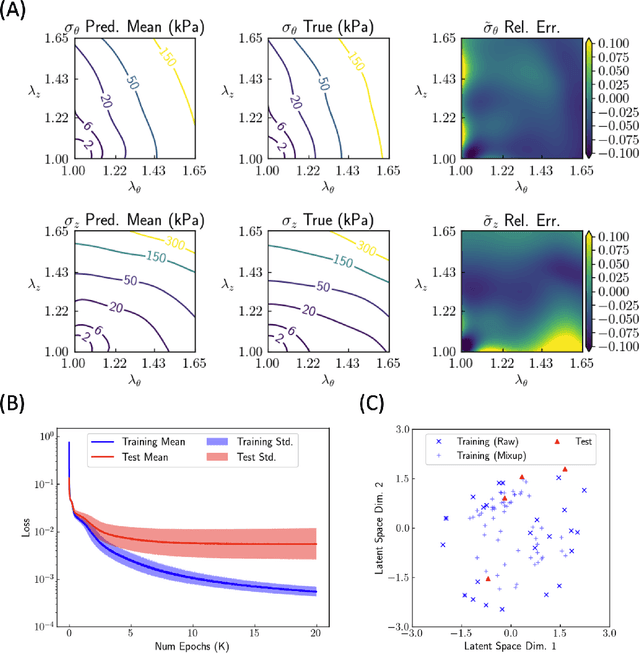
Many genetic mutations adversely affect the structure and function of load-bearing soft tissues, with clinical sequelae often responsible for disability or death. Parallel advances in genetics and histomechanical characterization provide significant insight into these conditions, but there remains a pressing need to integrate such information. We present a novel genotype-to-biomechanical-phenotype neural network (G2{\Phi}net) for characterizing and classifying biomechanical properties of soft tissues, which serve as important functional readouts of tissue health or disease. We illustrate the utility of our approach by inferring the nonlinear, genotype-dependent constitutive behavior of the aorta for four mouse models involving defects or deficiencies in extracellular constituents. We show that G2{\Phi}net can infer the biomechanical response while simultaneously ascribing the associated genotype correctly by utilizing limited, noisy, and unstructured experimental data. More broadly, G2{\Phi}net provides a powerful method and a paradigm shift for correlating genotype and biomechanical phenotype quantitatively, promising a better understanding of their interplay in biological tissues.

Interfacing Finite Elements with Deep Neural Operators for Fast Multiscale Modeling of Mechanics Problems

Multiscale modeling is an effective approach for investigating multiphysics systems with largely disparate size features, where models with different resolutions or heterogeneous descriptions are coupled together for predicting the system's response. The solver with lower fidelity (coarse) is responsible for simulating domains with homogeneous features, whereas the expensive high-fidelity (fine) model describes microscopic features with refined discretization, often making the overall cost prohibitively high, especially for time-dependent problems. In this work, we explore the idea of multiscale modeling with machine learning and employ DeepONet, a neural operator, as an efficient surrogate of the expensive solver. DeepONet is trained offline using data acquired from the fine solver for learning the underlying and possibly unknown fine-scale dynamics. It is then coupled with standard PDE solvers for predicting the multiscale systems with new boundary/initial conditions in the coupling stage. The proposed framework significantly reduces the computational cost of multiscale simulations since the DeepONet inference cost is negligible, facilitating readily the incorporation of a plurality of interface conditions and coupling schemes. We present various benchmarks to assess accuracy and speedup, and in particular we develop a coupling algorithm for a time-dependent problem, and we also demonstrate coupling of a continuum model (finite element methods, FEM) with a neural operator representation of a particle system (Smoothed Particle Hydrodynamics, SPH) for a uniaxial tension problem with hyperelastic material. What makes this approach unique is that a well-trained over-parametrized DeepONet can generalize well and make predictions at a negligible cost.

Simulating progressive intramural damage leading to aortic dissection using an operator-regression neural network

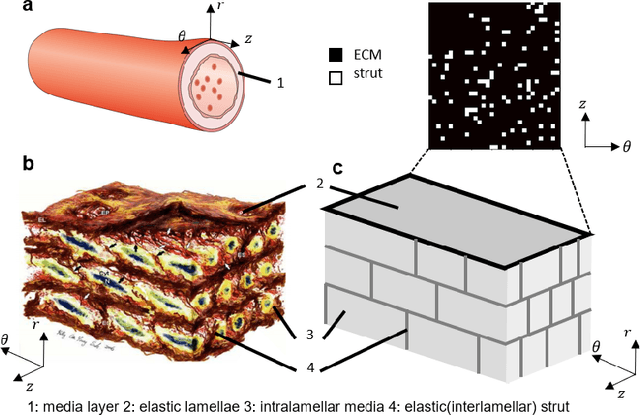
Aortic dissection progresses via delamination of the medial layer of the wall. Notwithstanding the complexity of this process, insight has been gleaned by studying in vitro and in silico the progression of dissection driven by quasi-static pressurization of the intramural space by fluid injection, which demonstrates that the differential propensity of dissection can be affected by spatial distributions of structurally significant interlamellar struts that connect adjacent elastic lamellae. In particular, diverse histological microstructures may lead to differential mechanical behavior during dissection, including the pressure--volume relationship of the injected fluid and the displacement field between adjacent lamellae. In this study, we develop a data-driven surrogate model for the delamination process for differential strut distributions using DeepONet, a new operator--regression neural network. The surrogate model is trained to predict the pressure--volume curve of the injected fluid and the damage progression field of the wall given a spatial distribution of struts, with in silico data generated with a phase-field finite element model. The results show that DeepONet can provide accurate predictions for diverse strut distributions, indicating that this composite branch-trunk neural network can effectively extract the underlying functional relationship between distinctive microstructures and their mechanical properties. More broadly, DeepONet can facilitate surrogate model-based analyses to quantify biological variability, improve inverse design, and predict mechanical properties based on multi-modality experimental data.

Physics-Informed Neural Networks for Nonhomogeneous Material Identification in Elasticity Imaging

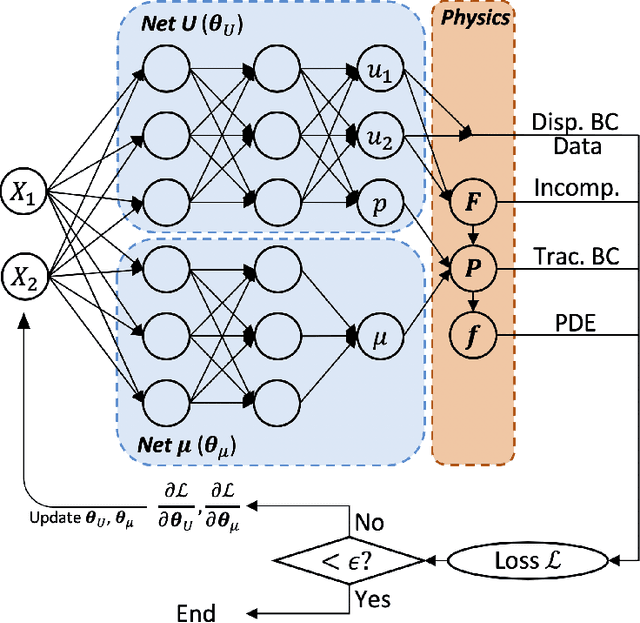
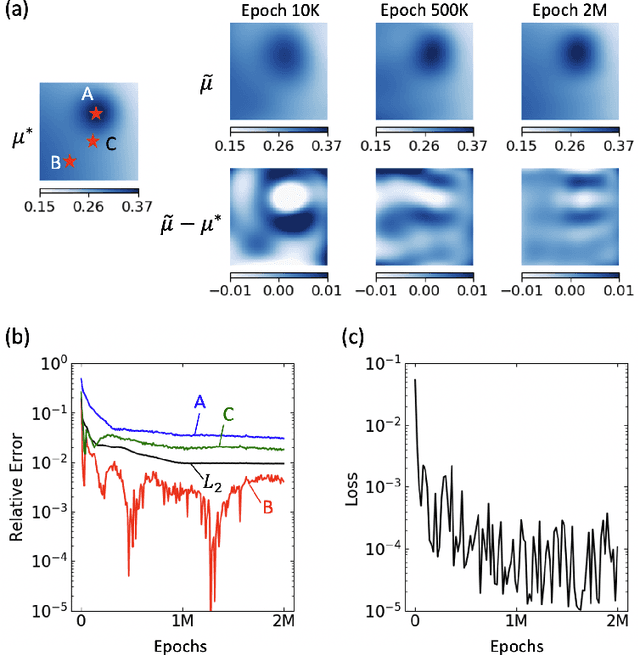
We apply Physics-Informed Neural Networks (PINNs) for solving identification problems of nonhomogeneous materials. We focus on the problem with a background in elasticity imaging, where one seeks to identify the nonhomogeneous mechanical properties of soft tissue based on the full-field displacement measurements under quasi-static loading. In our model, we apply two independent neural networks, one for approximating the solution of the corresponding forward problem, and the other for approximating the unknown material parameter field. As a proof of concept, we validate our model on a prototypical plane strain problem for incompressible hyperelastic tissue. The results show that the PINNs are effective in accurately recovering the unknown distribution of mechanical properties. By employing two neural networks in our model, we extend the capability of material identification of PINNs to include nonhomogeneous material parameter fields, which enables more flexibility of PINNs in representing complex material properties.