Convolutional Deep Operator Networks for Learning Nonlinear Focused Ultrasound Wave Propagation in Heterogeneous Spinal Cord Anatomy

Focused ultrasound (FUS) therapy is a promising tool for optimally targeted treatment of spinal cord injuries (SCI), offering submillimeter precision to enhance blood flow at injury sites while minimizing impact on surrounding tissues. However, its efficacy is highly sensitive to the placement of the ultrasound source, as the spinal cord's complex geometry and acoustic heterogeneity distort and attenuate the FUS signal. Current approaches rely on computer simulations to solve the governing wave propagation equations and compute patient-specific pressure maps using ultrasound images of the spinal cord anatomy. While accurate, these high-fidelity simulations are computationally intensive, taking up to hours to complete parameter sweeps, which is impractical for real-time surgical decision-making. To address this bottleneck, we propose a convolutional deep operator network (DeepONet) to rapidly predict FUS pressure fields in patient spinal cords. Unlike conventional neural networks, DeepONets are well equipped to approximate the solution operator of the parametric partial differential equations (PDEs) that govern the behavior of FUS waves with varying initial and boundary conditions (i.e., new transducer locations or spinal cord geometries) without requiring extensive simulations. Trained on simulated pressure maps across diverse patient anatomies, this surrogate model achieves real-time predictions with only a 2% loss on the test set, significantly accelerating the modeling of nonlinear physical systems in heterogeneous domains. By facilitating rapid parameter sweeps in surgical settings, this work provides a crucial step toward precise and individualized solutions in neurosurgical treatments.

Diffeomorphic Latent Neural Operators for Data-Efficient Learning of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (e.g., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Diffeomorphic Latent Neural Operator Learning for Data-Efficient Predictions of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (i.e., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

DIMON: Learning Solution Operators of Partial Differential Equations on a Diffeomorphic Family of Domains

The solution of a PDE over varying initial/boundary conditions on multiple domains is needed in a wide variety of applications, but it is computationally expensive if the solution is computed de novo whenever the initial/boundary conditions of the domain change. We introduce a general operator learning framework, called DIffeomorphic Mapping Operator learNing (DIMON) to learn approximate PDE solutions over a family of domains $\{\Omega_{\theta}}_\theta$, that learns the map from initial/boundary conditions and domain $\Omega_\theta$ to the solution of the PDE, or to specified functionals thereof. DIMON is based on transporting a given problem (initial/boundary conditions and domain $\Omega_{\theta}$) to a problem on a reference domain $\Omega_{0}$, where training data from multiple problems is used to learn the map to the solution on $\Omega_{0}$, which is then re-mapped to the original domain $\Omega_{\theta}$. We consider several problems to demonstrate the performance of the framework in learning both static and time-dependent PDEs on non-rigid geometries; these include solving the Laplace equation, reaction-diffusion equations, and a multiscale PDE that characterizes the electrical propagation on the left ventricle. This work paves the way toward the fast prediction of PDE solutions on a family of domains and the application of neural operators in engineering and precision medicine.

A Generative Modeling Framework for Inferring Families of Biomechanical Constitutive Laws in Data-Sparse Regimes

Quantifying biomechanical properties of the human vasculature could deepen our understanding of cardiovascular diseases. Standard nonlinear regression in constitutive modeling requires considerable high-quality data and an explicit form of the constitutive model as prior knowledge. By contrast, we propose a novel approach that combines generative deep learning with Bayesian inference to efficiently infer families of constitutive relationships in data-sparse regimes. Inspired by the concept of functional priors, we develop a generative adversarial network (GAN) that incorporates a neural operator as the generator and a fully-connected neural network as the discriminator. The generator takes a vector of noise conditioned on measurement data as input and yields the predicted constitutive relationship, which is scrutinized by the discriminator in the following step. We demonstrate that this framework can accurately estimate means and standard deviations of the constitutive relationships of the murine aorta using data collected either from model-generated synthetic data or ex vivo experiments for mice with genetic deficiencies. In addition, the framework learns priors of constitutive models without explicitly knowing their functional form, providing a new model-agnostic approach to learning hidden constitutive behaviors from data.

Interfacing Finite Elements with Deep Neural Operators for Fast Multiscale Modeling of Mechanics Problems

Multiscale modeling is an effective approach for investigating multiphysics systems with largely disparate size features, where models with different resolutions or heterogeneous descriptions are coupled together for predicting the system's response. The solver with lower fidelity (coarse) is responsible for simulating domains with homogeneous features, whereas the expensive high-fidelity (fine) model describes microscopic features with refined discretization, often making the overall cost prohibitively high, especially for time-dependent problems. In this work, we explore the idea of multiscale modeling with machine learning and employ DeepONet, a neural operator, as an efficient surrogate of the expensive solver. DeepONet is trained offline using data acquired from the fine solver for learning the underlying and possibly unknown fine-scale dynamics. It is then coupled with standard PDE solvers for predicting the multiscale systems with new boundary/initial conditions in the coupling stage. The proposed framework significantly reduces the computational cost of multiscale simulations since the DeepONet inference cost is negligible, facilitating readily the incorporation of a plurality of interface conditions and coupling schemes. We present various benchmarks to assess accuracy and speedup, and in particular we develop a coupling algorithm for a time-dependent problem, and we also demonstrate coupling of a continuum model (finite element methods, FEM) with a neural operator representation of a particle system (Smoothed Particle Hydrodynamics, SPH) for a uniaxial tension problem with hyperelastic material. What makes this approach unique is that a well-trained over-parametrized DeepONet can generalize well and make predictions at a negligible cost.

Simulating progressive intramural damage leading to aortic dissection using an operator-regression neural network

Aortic dissection progresses via delamination of the medial layer of the wall. Notwithstanding the complexity of this process, insight has been gleaned by studying in vitro and in silico the progression of dissection driven by quasi-static pressurization of the intramural space by fluid injection, which demonstrates that the differential propensity of dissection can be affected by spatial distributions of structurally significant interlamellar struts that connect adjacent elastic lamellae. In particular, diverse histological microstructures may lead to differential mechanical behavior during dissection, including the pressure--volume relationship of the injected fluid and the displacement field between adjacent lamellae. In this study, we develop a data-driven surrogate model for the delamination process for differential strut distributions using DeepONet, a new operator--regression neural network. The surrogate model is trained to predict the pressure--volume curve of the injected fluid and the damage progression field of the wall given a spatial distribution of struts, with in silico data generated with a phase-field finite element model. The results show that DeepONet can provide accurate predictions for diverse strut distributions, indicating that this composite branch-trunk neural network can effectively extract the underlying functional relationship between distinctive microstructures and their mechanical properties. More broadly, DeepONet can facilitate surrogate model-based analyses to quantify biological variability, improve inverse design, and predict mechanical properties based on multi-modality experimental data.

A physics-informed variational DeepONet for predicting the crack path in brittle materials

Failure trajectories, identifying the probable failure zones, and damage statistics are some of the key quantities of relevance in brittle fracture applications. High-fidelity numerical solvers that reliably estimate these relevant quantities exist but they are computationally demanding requiring a high resolution of the crack. Moreover, independent intensive simulations need to be carried out even for a small change in domain parameters and/or material properties. Therefore, fast and generalizable surrogate models are needed to alleviate the computational burden but the discontinuous nature of fracture mechanics presents a major challenge to developing such models. We propose a physics-informed variational formulation of DeepONet (V-DeepONet) for brittle fracture analysis. V-DeepONet is trained to map the initial configuration of the defect to the relevant fields of interests (e.g., damage and displacement fields). Once the network is trained, the entire global solution can be rapidly obtained for any initial crack configuration and loading steps on that domain. While the original DeepONet is solely data-driven, we take a different path to train the V-DeepONet by imposing the governing equations in variational form and we also use some labelled data. We demonstrate the effectiveness of V-DeepOnet through two benchmarks of brittle fracture, and we verify its accuracy using results from high-fidelity solvers. Encoding the physical laws and also some data to train the network renders the surrogate model capable of accurately performing both interpolation and extrapolation tasks, considering that fracture modeling is very sensitive to fluctuations. The proposed hybrid training of V-DeepONet is superior to state-of-the-art methods and can be applied to a wide array of dynamical systems with complex responses.

Physics-informed neural networks (PINNs) for fluid mechanics: A review

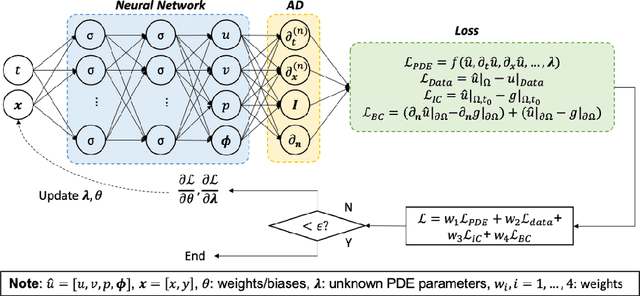
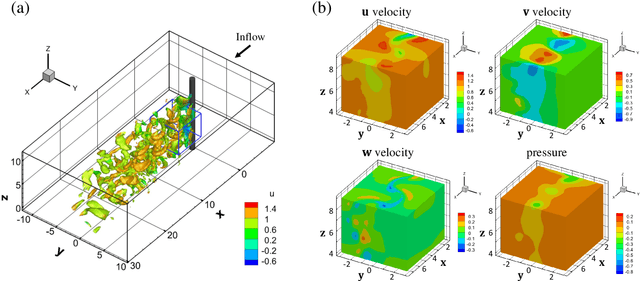
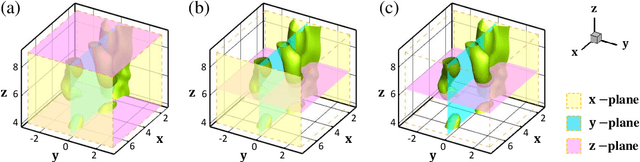
Despite the significant progress over the last 50 years in simulating flow problems using numerical discretization of the Navier-Stokes equations (NSE), we still cannot incorporate seamlessly noisy data into existing algorithms, mesh-generation is complex, and we cannot tackle high-dimensional problems governed by parametrized NSE. Moreover, solving inverse flow problems is often prohibitively expensive and requires complex and expensive formulations and new computer codes. Here, we review flow physics-informed learning, integrating seamlessly data and mathematical models, and implementing them using physics-informed neural networks (PINNs). We demonstrate the effectiveness of PINNs for inverse problems related to three-dimensional wake flows, supersonic flows, and biomedical flows.

Physics-Informed Neural Networks for Nonhomogeneous Material Identification in Elasticity Imaging

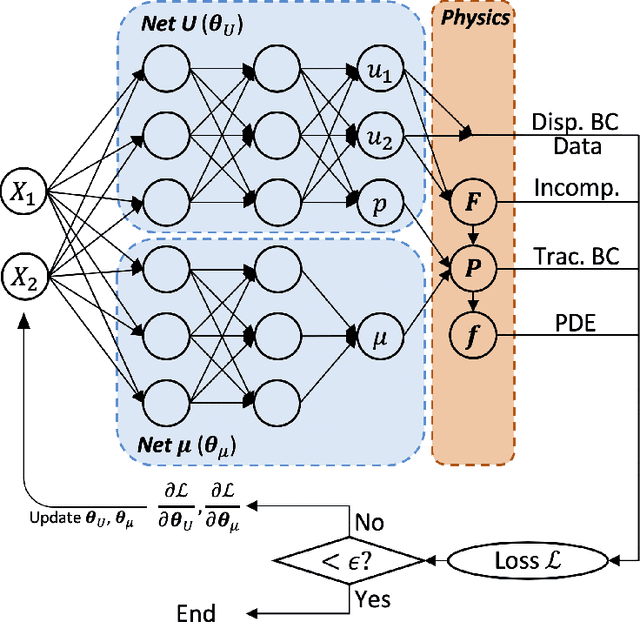
We apply Physics-Informed Neural Networks (PINNs) for solving identification problems of nonhomogeneous materials. We focus on the problem with a background in elasticity imaging, where one seeks to identify the nonhomogeneous mechanical properties of soft tissue based on the full-field displacement measurements under quasi-static loading. In our model, we apply two independent neural networks, one for approximating the solution of the corresponding forward problem, and the other for approximating the unknown material parameter field. As a proof of concept, we validate our model on a prototypical plane strain problem for incompressible hyperelastic tissue. The results show that the PINNs are effective in accurately recovering the unknown distribution of mechanical properties. By employing two neural networks in our model, we extend the capability of material identification of PINNs to include nonhomogeneous material parameter fields, which enables more flexibility of PINNs in representing complex material properties.