Diffeomorphic Latent Neural Operators for Data-Efficient Learning of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (e.g., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Diffeomorphic Latent Neural Operator Learning for Data-Efficient Predictions of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (i.e., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Fourier Spectral Physics Informed Neural Network: An Efficient and Low-Memory PINN

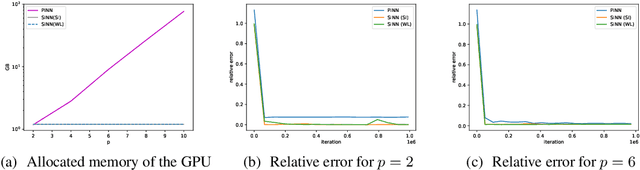
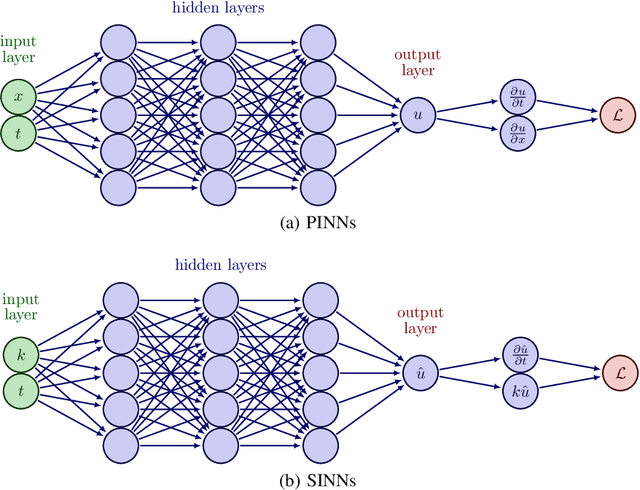
With growing investigations into solving partial differential equations by physics-informed neural networks (PINNs), more accurate and efficient PINNs are required to meet the practical demands of scientific computing. One bottleneck of current PINNs is computing the high-order derivatives via automatic differentiation which often necessitates substantial computing resources. In this paper, we focus on removing the automatic differentiation of the spatial derivatives and propose a spectral-based neural network that substitutes the differential operator with a multiplication. Compared to the PINNs, our approach requires lower memory and shorter training time. Thanks to the exponential convergence of the spectral basis, our approach is more accurate. Moreover, to handle the different situations between physics domain and spectral domain, we provide two strategies to train networks by their spectral information. Through a series of comprehensive experiments, We validate the aforementioned merits of our proposed network.

Early Risk Assessment Model for ICA Timing Strategy in Unstable Angina Patients Using Multi-Modal Machine Learning

Background: Invasive coronary arteriography (ICA) is recognized as the gold standard for diagnosing cardiovascular diseases, including unstable angina (UA). The challenge lies in determining the optimal timing for ICA in UA patients, balancing the need for revascularization in high-risk patients against the potential complications in low-risk ones. Unlike myocardial infarction, UA does not have specific indicators like ST-segment deviation or cardiac enzymes, making risk assessment complex. Objectives: Our study aims to enhance the early risk assessment for UA patients by utilizing machine learning algorithms. These algorithms can potentially identify patients who would benefit most from ICA by analyzing less specific yet related indicators that are challenging for human physicians to interpret. Methods: We collected data from 640 UA patients at Shanghai General Hospital, including medical history and electrocardiograms (ECG). Machine learning algorithms were trained using multi-modal demographic characteristics including clinical risk factors, symptoms, biomarker levels, and ECG features extracted by pre-trained neural networks. The goal was to stratify patients based on their revascularization risk. Additionally, we translated our models into applicable and explainable look-up tables through discretization for practical clinical use. Results: The study achieved an Area Under the Curve (AUC) of $0.719 \pm 0.065$ in risk stratification, significantly surpassing the widely adopted GRACE score's AUC of $0.579 \pm 0.044$. Conclusions: The results suggest that machine learning can provide superior risk stratification for UA patients. This improved stratification could help in balancing the risks, costs, and complications associated with ICA, indicating a potential shift in clinical assessment practices for unstable angina.

SLR: Learning Quadruped Locomotion without Privileged Information

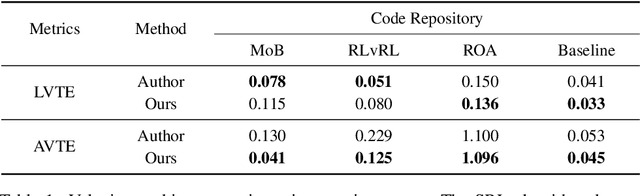
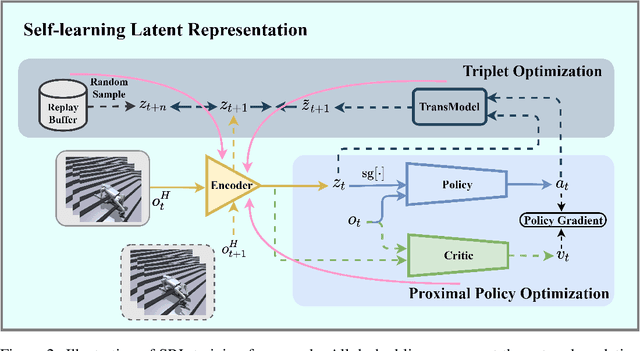
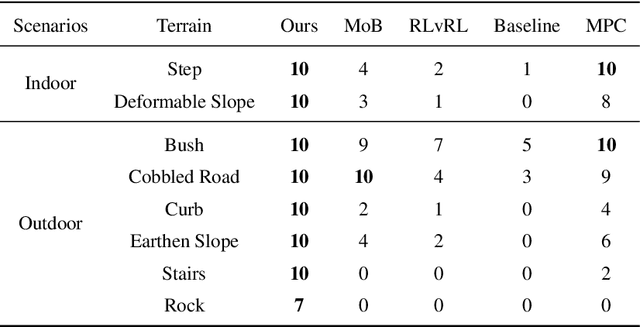
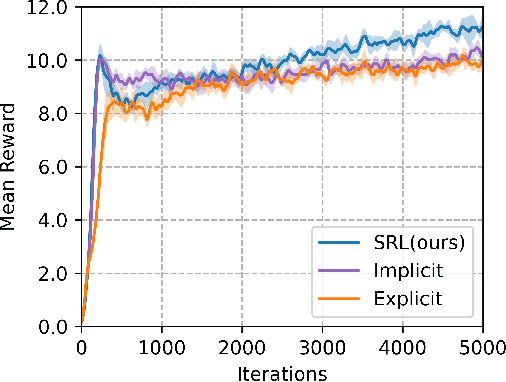
Traditional reinforcement learning control for quadruped robots often relies on privileged information, demanding meticulous selection and precise estimation, thereby imposing constraints on the development process. This work proposes a Self-learning Latent Representation (SLR) method, which achieves high-performance control policy learning without the need for privileged information. To enhance the credibility of our proposed method's evaluation, SLR is compared with open-source code repositories of state-of-the-art algorithms, retaining the original authors' configuration parameters. Across four repositories, SLR consistently outperforms the reference results. Ultimately, the trained policy and encoder empower the quadruped robot to navigate steps, climb stairs, ascend rocks, and traverse various challenging terrains. Robot experiment videos are at https://11chens.github.io/SLR/

Discovering an interpretable mathematical expression for a full wind-turbine wake with artificial intelligence enhanced symbolic regression

The rapid expansion of wind power worldwide underscores the critical significance of engineering-focused analytical wake models in both the design and operation of wind farms. These theoretically-derived ana lytical wake models have limited predictive capabilities, particularly in the near-wake region close to the turbine rotor, due to assumptions that do not hold. Knowledge discovery methods can bridge these gaps by extracting insights, adjusting for theoretical assumptions, and developing accurate models for physical processes. In this study, we introduce a genetic symbolic regression (SR) algorithm to discover an interpretable mathematical expression for the mean velocity deficit throughout the wake, a previously unavailable insight. By incorporating a double Gaussian distribution into the SR algorithm as domain knowledge and designing a hierarchical equation structure, the search space is reduced, thus efficiently finding a concise, physically informed, and robust wake model. The proposed mathematical expression (equation) can predict the wake velocity deficit at any location in the full-wake region with high precision and stability. The model's effectiveness and practicality are validated through experimental data and high-fidelity numerical simulations.

Filtered Partial Differential Equations: a robust surrogate constraint in physics-informed deep learning framework

Embedding physical knowledge into neural network (NN) training has been a hot topic. However, when facing the complex real-world, most of the existing methods still strongly rely on the quantity and quality of observation data. Furthermore, the neural networks often struggle to converge when the solution to the real equation is very complex. Inspired by large eddy simulation in computational fluid dynamics, we propose an improved method based on filtering. We analyzed the causes of the difficulties in physics informed machine learning, and proposed a surrogate constraint (filtered PDE, FPDE in short) of the original physical equations to reduce the influence of noisy and sparse observation data. In the noise and sparsity experiment, the proposed FPDE models (which are optimized by FPDE constraints) have better robustness than the conventional PDE models. Experiments demonstrate that the FPDE model can obtain the same quality solution with 100% higher noise and 12% quantity of observation data of the baseline. Besides, two groups of real measurement data are used to show the FPDE improvements in real cases. The final results show that FPDE still gives more physically reasonable solutions when facing the incomplete equation problem and the extremely sparse and high-noise conditions. For combining real-world experiment data into physics-informed training, the proposed FPDE constraint is useful and performs well in two real-world experiments: modeling the blood velocity in vessels and cell migration in scratches.

Stabilizing the Maximal Entropy Moment Method for Rarefied Gas Dynamics at Single-Precision

Developing extended hydrodynamics equations valid for both dense and rarefied gases remains a great challenge. A systematical solution for this challenge is the moment method describing both dense and rarefied gas behaviors with moments of gas molecule velocity distributions. Among moment methods, the maximal entropy moment method (MEM) stands out for its well-posedness and stability, which utilizes velocity distributions with maximized entropy. However, finding such distributions requires solving an ill-conditioned and computation-demanding optimization problem. This problem causes numerical overflow and breakdown when the numerical precision is insufficient, especially for flows like high-speed shock waves. It also prevents modern GPUs from accelerating optimization with their enormous single floating-point precision computation power. This paper aims to stabilize MEM, making it practical for simulating very strong normal shock waves on modern GPUs at single precision. We propose the gauge transformations for MEM, making the optimization less ill-conditioned. We also tackle numerical overflow and breakdown by adopting the canonical form of distribution and Newton's modified optimization method. With these techniques, we achieved a single-precision GPU simulation of a Mach 10 shock wave with 35 moments MEM, surpassing the previous double-precision results of Mach 4. Moreover, we argued that over-refined spatial mesh degrades both the accuracy and stability of MEM. Overall, this paper makes the maximal entropy moment method practical for simulating very strong normal shock waves on modern GPUs at single-precision, with significant stability improvement compared to previous methods.

Graph Partner Neural Networks for Semi-Supervised Learning on Graphs

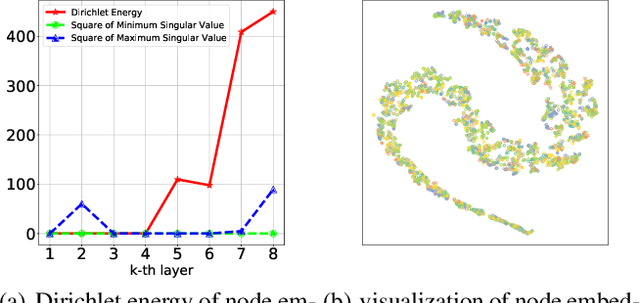
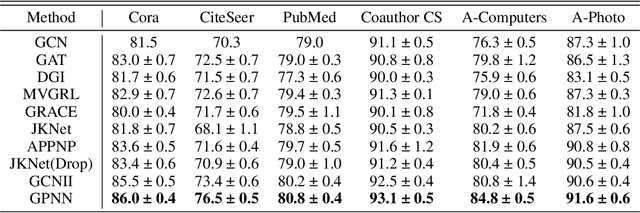
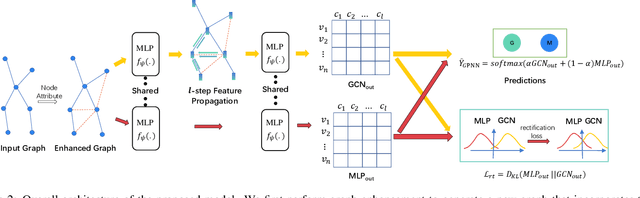
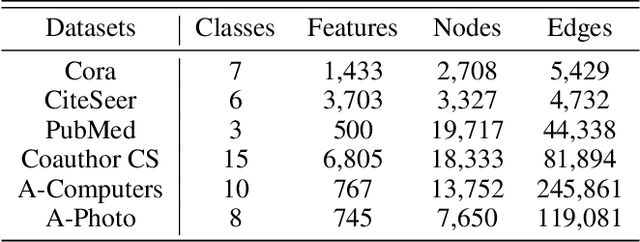
Graph Convolutional Networks (GCNs) are powerful for processing graph-structured data and have achieved state-of-the-art performance in several tasks such as node classification, link prediction, and graph classification. However, it is inevitable for deep GCNs to suffer from an over-smoothing issue that the representations of nodes will tend to be indistinguishable after repeated graph convolution operations. To address this problem, we propose the Graph Partner Neural Network (GPNN) which incorporates a de-parameterized GCN and a parameter-sharing MLP. We provide empirical and theoretical evidence to demonstrate the effectiveness of the proposed MLP partner on tackling over-smoothing while benefiting from appropriate smoothness. To further tackle over-smoothing and regulate the learning process, we introduce a well-designed consistency contrastive loss and KL divergence loss. Besides, we present a graph enhancement technique to improve the overall quality of edges in graphs. While most GCNs can work with shallow architecture only, GPNN can obtain better results through increasing model depth. Experiments on various node classification tasks have demonstrated the state-of-the-art performance of GPNN. Meanwhile, extensive ablation studies are conducted to investigate the contributions of each component in tackling over-smoothing and improving performance.

Data Driven Macroscopic Modeling across Knudsen Numbers for Rarefied Gas Dynamics and Application to Rayleigh Scattering

Macroscopic modeling of the gas dynamics across Knudsen numbers from dense gas region to rarefied gas region remains a great challenge. The reason is macroscopic models lack accurate constitutive relations valid across different Knudsen numbers. To address this problem, we proposed a Data-driven, KnUdsen number Adaptive Linear constitutive relation model named DUAL. The DUAL model is accurate across a range of Knudsen numbers, from dense to rarefied, through learning to adapt Knudsen number change from observed data. It is consistent with the Navier-Stokes equation under the hydrodynamic limit, by utilizing a constrained neural network. In addition, it naturally satisfies the second law of thermodynamics and is robust to noisy data. We test the DUAL model on the calculation of Rayleigh scattering spectra. The DUAL model gives accurate spectra for various Knudsen numbers and is superior to traditional perturbation and moment expansion methods.