100-LongBench: Are de facto Long-Context Benchmarks Literally Evaluating Long-Context Ability?

Long-context capability is considered one of the most important abilities of LLMs, as a truly long context-capable LLM enables users to effortlessly process many originally exhausting tasks -- e.g., digesting a long-form document to find answers vs. directly asking an LLM about it. However, existing real-task-based long-context evaluation benchmarks have two major shortcomings. First, benchmarks like LongBench often do not provide proper metrics to separate long-context performance from the model's baseline ability, making cross-model comparison unclear. Second, such benchmarks are usually constructed with fixed input lengths, which limits their applicability across different models and fails to reveal when a model begins to break down. To address these issues, we introduce a length-controllable long-context benchmark and a novel metric that disentangles baseline knowledge from true long-context capabilities. Experiments demonstrate the superiority of our approach in effectively evaluating LLMs.

Longer Context, Deeper Thinking: Uncovering the Role of Long-Context Ability in Reasoning

Recent language models exhibit strong reasoning capabilities, yet the influence of long-context capacity on reasoning remains underexplored. In this work, we hypothesize that current limitations in reasoning stem, in part, from insufficient long-context capacity, motivated by empirical observations such as (1) higher context window length often leads to stronger reasoning performance, and (2) failed reasoning cases resemble failed long-context cases. To test this hypothesis, we examine whether enhancing a model's long-context ability before Supervised Fine-Tuning (SFT) leads to improved reasoning performance. Specifically, we compared models with identical architectures and fine-tuning data but varying levels of long-context capacity. Our results reveal a consistent trend: models with stronger long-context capacity achieve significantly higher accuracy on reasoning benchmarks after SFT. Notably, these gains persist even on tasks with short input lengths, indicating that long-context training offers generalizable benefits for reasoning performance. These findings suggest that long-context modeling is not just essential for processing lengthy inputs, but also serves as a critical foundation for reasoning. We advocate for treating long-context capacity as a first-class objective in the design of future language models.

SELF: Self-Extend the Context Length With Logistic Growth Function

Large language models suffer issues when operated on long contexts that are larger than their training context length due to the standard position encoding for tokens in the attention layer. Tokens a long distance apart will rarely have an effect on each other and long prompts yield unexpected results. To solve this problem, we propose SELF (Self-Extend the Context Length With Logistic Growth Function): a solution of grouping consecutive tokens at varying group sizes using a logistic capacity equation combined with a constant group size at smaller relative distances. Our model had an increase in performance of up to 12% compared to the LongLM extension method in LEval (specifically on the Qwen model). On summarization related tasks in LongBench, our model performed up to 6.4% better than LongLM (specifically on the Llama-2-7b model). On reading comprehension tasks from LEval, our model performed up to 5.4% better than the LongLM. Our code is available at https://github.com/alexeipc/SELF-LLM.

Speculative Thinking: Enhancing Small-Model Reasoning with Large Model Guidance at Inference Time

Recent advances leverage post-training to enhance model reasoning performance, which typically requires costly training pipelines and still suffers from inefficient, overly lengthy outputs. We introduce Speculative Thinking, a training-free framework that enables large reasoning models to guide smaller ones during inference at the reasoning level, distinct from speculative decoding, which operates at the token level. Our approach is based on two observations: (1) reasoning-supportive tokens such as "wait" frequently appear after structural delimiters like "\n\n", serving as signals for reflection or continuation; and (2) larger models exhibit stronger control over reflective behavior, reducing unnecessary backtracking while improving reasoning quality. By strategically delegating reflective steps to a more capable model, our method significantly boosts the reasoning accuracy of reasoning models while shortening their output. With the assistance of the 32B reasoning model, the 1.5B model's accuracy on MATH500 increases from 83.2% to 89.4%, marking a substantial improvement of 6.2%. Simultaneously, the average output length is reduced from 5439 tokens to 4583 tokens, representing a 15.7% decrease. Moreover, when applied to a non-reasoning model (Qwen-2.5-7B-Instruct), our framework boosts its accuracy from 74.0% to 81.8% on the same benchmark, achieving a relative improvement of 7.8%.

Thinking Preference Optimization

Supervised Fine-Tuning (SFT) has been a go-to and effective method for enhancing long chain-of-thought (CoT) reasoning in relatively small LLMs by fine-tuning them with long CoT responses from larger LLMs. To continually improve reasoning abilities, we can either collect new high-quality long CoT reasoning SFT data or repeatedly train on existing SFT datasets. However, acquiring new long CoT SFT data is costly and limited, while repeated training often results in a performance plateau or decline. To further boost the performance with the SFT data, we propose Thinking Preference Optimization (ThinkPO), a simple yet effective post-SFT method that enhances long CoT reasoning without requiring new long CoT responses. Instead, ThinkPO utilizes readily available or easily obtainable short CoT reasoning responses as rejected answers and long CoT responses as chosen answers for the same question. It then applies direct preference optimization to encourage the model to favor longer reasoning outputs. Experiments show that ThinkPO further improves the reasoning performance of SFT-ed models, e.g. it increases math reasoning accuracy of SFT-ed models by 8.6% and output length by 25.9%. Notably, ThinkPO is capable of continually boosting the performance of the publicly distilled SFT model, e.g., increasing the official DeepSeek-R1-Distill-Qwen-7B's performance on MATH500 from 87.4% to 91.2%.

Linear building pattern recognition via spatial knowledge graph

Building patterns are important urban structures that reflect the effect of the urban material and social-economic on a region. Previous researches are mostly based on the graph isomorphism method and use rules to recognize building patterns, which are not efficient. The knowledge graph uses the graph to model the relationship between entities, and specific subgraph patterns can be efficiently obtained by using relevant reasoning tools. Thus, we try to apply the knowledge graph to recognize linear building patterns. First, we use the property graph to express the spatial relations in proximity, similar and linear arrangement between buildings; secondly, the rules of linear pattern recognition are expressed as the rules of knowledge graph reasoning; finally, the linear building patterns are recognized by using the rule-based reasoning in the built knowledge graph. The experimental results on a dataset containing 1289 buildings show that the method in this paper can achieve the same precision and recall as the existing methods; meanwhile, the recognition efficiency is improved by 5.98 times.

Stabilizing the Maximal Entropy Moment Method for Rarefied Gas Dynamics at Single-Precision

Developing extended hydrodynamics equations valid for both dense and rarefied gases remains a great challenge. A systematical solution for this challenge is the moment method describing both dense and rarefied gas behaviors with moments of gas molecule velocity distributions. Among moment methods, the maximal entropy moment method (MEM) stands out for its well-posedness and stability, which utilizes velocity distributions with maximized entropy. However, finding such distributions requires solving an ill-conditioned and computation-demanding optimization problem. This problem causes numerical overflow and breakdown when the numerical precision is insufficient, especially for flows like high-speed shock waves. It also prevents modern GPUs from accelerating optimization with their enormous single floating-point precision computation power. This paper aims to stabilize MEM, making it practical for simulating very strong normal shock waves on modern GPUs at single precision. We propose the gauge transformations for MEM, making the optimization less ill-conditioned. We also tackle numerical overflow and breakdown by adopting the canonical form of distribution and Newton's modified optimization method. With these techniques, we achieved a single-precision GPU simulation of a Mach 10 shock wave with 35 moments MEM, surpassing the previous double-precision results of Mach 4. Moreover, we argued that over-refined spatial mesh degrades both the accuracy and stability of MEM. Overall, this paper makes the maximal entropy moment method practical for simulating very strong normal shock waves on modern GPUs at single-precision, with significant stability improvement compared to previous methods.

Advbox: a toolbox to generate adversarial examples that fool neural networks

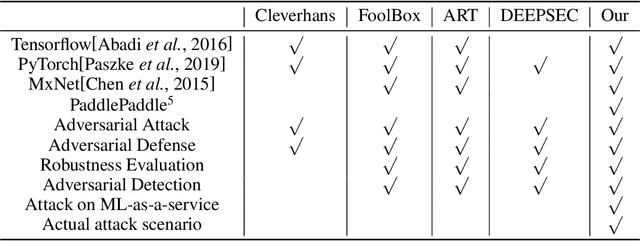
In recent years, neural networks have been extensively deployed for computer vision tasks, particularly visual classification problems, where new algorithms reported to achieve or even surpass the human performance. Recent studies have shown that they are all vulnerable to the attack of adversarial examples. Small and often imperceptible perturbations to the input images are sufficient to fool the most powerful neural networks. \emph{Advbox} is a toolbox to generate adversarial examples that fool neural networks in PaddlePaddle, PyTorch, Caffe2, MxNet, Keras, TensorFlow and it can benchmark the robustness of machine learning models. Compared to previous work, our platform supports black box attacks on Machine-Learning-as-a-service, as well as more attack scenarios, such as Face Recognition Attack, Stealth T-shirt, and DeepFake Face Detect. The code is licensed under the Apache 2.0 and is openly available at https://github.com/advboxes/AdvBox. Advbox now supports Python 3.