VQualA 2025 Challenge on Visual Quality Comparison for Large Multimodal Models: Methods and Results

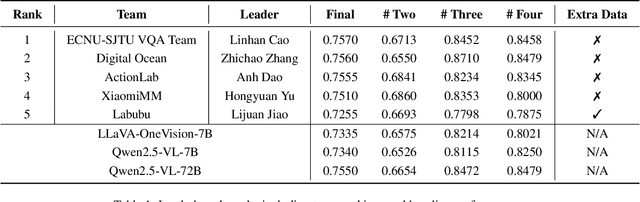
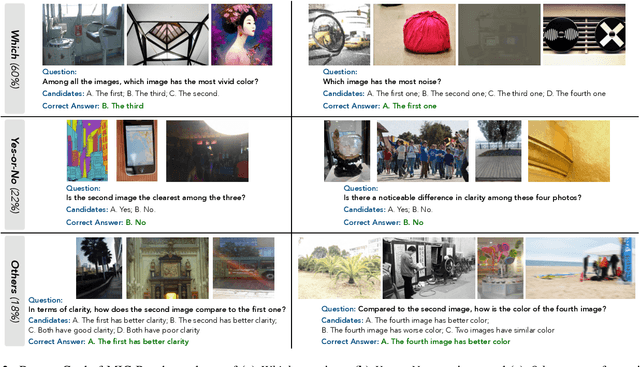
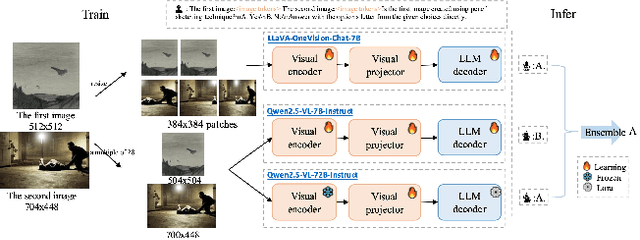
This paper presents a summary of the VQualA 2025 Challenge on Visual Quality Comparison for Large Multimodal Models (LMMs), hosted as part of the ICCV 2025 Workshop on Visual Quality Assessment. The challenge aims to evaluate and enhance the ability of state-of-the-art LMMs to perform open-ended and detailed reasoning about visual quality differences across multiple images. To this end, the competition introduces a novel benchmark comprising thousands of coarse-to-fine grained visual quality comparison tasks, spanning single images, pairs, and multi-image groups. Each task requires models to provide accurate quality judgments. The competition emphasizes holistic evaluation protocols, including 2AFC-based binary preference and multi-choice questions (MCQs). Around 100 participants submitted entries, with five models demonstrating the emerging capabilities of instruction-tuned LMMs on quality assessment. This challenge marks a significant step toward open-domain visual quality reasoning and comparison and serves as a catalyst for future research on interpretable and human-aligned quality evaluation systems.

FUSE: Measure-Theoretic Compact Fuzzy Set Representation for Taxonomy Expansion

Taxonomy Expansion, which models complex concepts and their relations, can be formulated as a set representation learning task. The generalization of set, fuzzy set, incorporates uncertainty and measures the information within a semantic concept, making it suitable for concept modeling. Existing works usually model sets as vectors or geometric objects such as boxes, which are not closed under set operations. In this work, we propose a sound and efficient formulation of set representation learning based on its volume approximation as a fuzzy set. The resulting embedding framework, Fuzzy Set Embedding (FUSE), satisfies all set operations and compactly approximates the underlying fuzzy set, hence preserving information while being efficient to learn, relying on minimum neural architecture. We empirically demonstrate the power of FUSE on the task of taxonomy expansion, where FUSE achieves remarkable improvements up to 23% compared with existing baselines. Our work marks the first attempt to understand and efficiently compute the embeddings of fuzzy sets.

100-LongBench: Are de facto Long-Context Benchmarks Literally Evaluating Long-Context Ability?

Long-context capability is considered one of the most important abilities of LLMs, as a truly long context-capable LLM enables users to effortlessly process many originally exhausting tasks -- e.g., digesting a long-form document to find answers vs. directly asking an LLM about it. However, existing real-task-based long-context evaluation benchmarks have two major shortcomings. First, benchmarks like LongBench often do not provide proper metrics to separate long-context performance from the model's baseline ability, making cross-model comparison unclear. Second, such benchmarks are usually constructed with fixed input lengths, which limits their applicability across different models and fails to reveal when a model begins to break down. To address these issues, we introduce a length-controllable long-context benchmark and a novel metric that disentangles baseline knowledge from true long-context capabilities. Experiments demonstrate the superiority of our approach in effectively evaluating LLMs.

SWEET-RL: Training Multi-Turn LLM Agents on Collaborative Reasoning Tasks

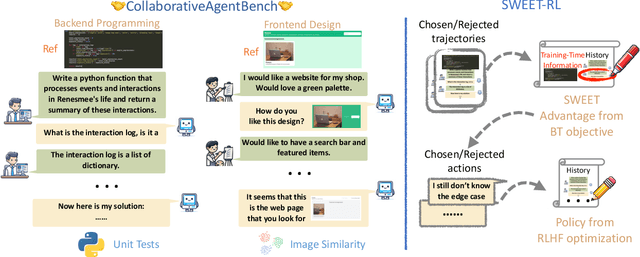
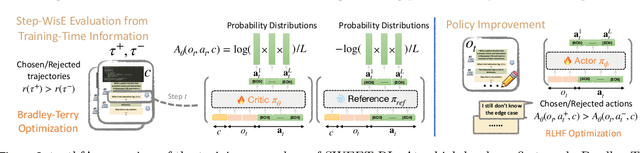
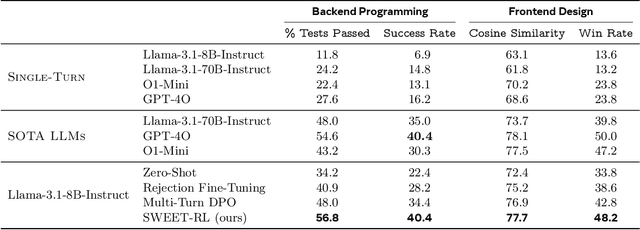
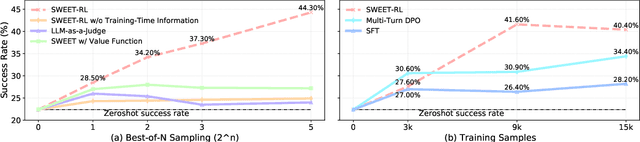
Large language model (LLM) agents need to perform multi-turn interactions in real-world tasks. However, existing multi-turn RL algorithms for optimizing LLM agents fail to perform effective credit assignment over multiple turns while leveraging the generalization capabilities of LLMs and it remains unclear how to develop such algorithms. To study this, we first introduce a new benchmark, ColBench, where an LLM agent interacts with a human collaborator over multiple turns to solve realistic tasks in backend programming and frontend design. Building on this benchmark, we propose a novel RL algorithm, SWEET-RL (RL with Step-WisE Evaluation from Training-time information), that uses a carefully designed optimization objective to train a critic model with access to additional training-time information. The critic provides step-level rewards for improving the policy model. Our experiments demonstrate that SWEET-RL achieves a 6% absolute improvement in success and win rates on ColBench compared to other state-of-the-art multi-turn RL algorithms, enabling Llama-3.1-8B to match or exceed the performance of GPT4-o in realistic collaborative content creation.

NaturalReasoning: Reasoning in the Wild with 2.8M Challenging Questions

Scaling reasoning capabilities beyond traditional domains such as math and coding is hindered by the lack of diverse and high-quality questions. To overcome this limitation, we introduce a scalable approach for generating diverse and challenging reasoning questions, accompanied by reference answers. We present NaturalReasoning, a comprehensive dataset comprising 2.8 million questions that span multiple domains, including STEM fields (e.g., Physics, Computer Science), Economics, Social Sciences, and more. We demonstrate the utility of the questions in NaturalReasoning through knowledge distillation experiments which show that NaturalReasoning can effectively elicit and transfer reasoning capabilities from a strong teacher model. Furthermore, we demonstrate that NaturalReasoning is also effective for unsupervised self-training using external reward models or self-rewarding.

Towards Full Delegation: Designing Ideal Agentic Behaviors for Travel Planning

How are LLM-based agents used in the future? While many of the existing work on agents has focused on improving the performance of a specific family of objective and challenging tasks, in this work, we take a different perspective by thinking about full delegation: agents take over humans' routine decision-making processes and are trusted by humans to find solutions that fit people's personalized needs and are adaptive to ever-changing context. In order to achieve such a goal, the behavior of the agents, i.e., agentic behaviors, should be evaluated not only on their achievements (i.e., outcome evaluation), but also how they achieved that (i.e., procedure evaluation). For this, we propose APEC Agent Constitution, a list of criteria that an agent should follow for good agentic behaviors, including Accuracy, Proactivity, Efficiency and Credibility. To verify whether APEC aligns with human preferences, we develop APEC-Travel, a travel planning agent that proactively extracts hidden personalized needs via multi-round dialog with travelers. APEC-Travel is constructed purely from synthetic data generated by Llama3.1-405B-Instruct with a diverse set of travelers' persona to simulate rich distribution of dialogs. Iteratively fine-tuned to follow APEC Agent Constitution, APEC-Travel surpasses baselines by 20.7% on rule-based metrics and 9.1% on LLM-as-a-Judge scores across the constitution axes.

To the Globe (TTG): Towards Language-Driven Guaranteed Travel Planning

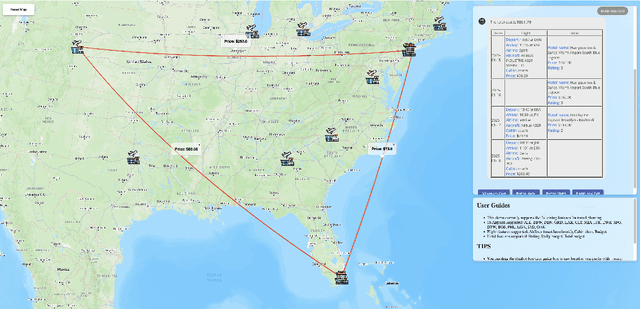
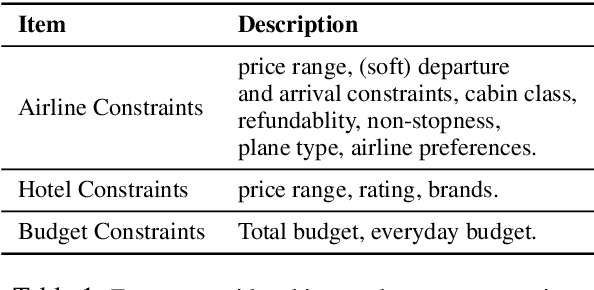
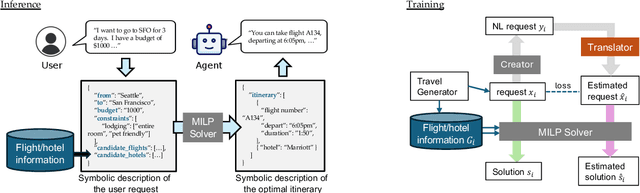
Travel planning is a challenging and time-consuming task that aims to find an itinerary which satisfies multiple, interdependent constraints regarding flights, accommodations, attractions, and other travel arrangements. In this paper, we propose To the Globe (TTG), a real-time demo system that takes natural language requests from users, translates it to symbolic form via a fine-tuned Large Language Model, and produces optimal travel itineraries with Mixed Integer Linear Programming solvers. The overall system takes ~5 seconds to reply to the user request with guaranteed itineraries. To train TTG, we develop a synthetic data pipeline that generates user requests, flight and hotel information in symbolic form without human annotations, based on the statistics of real-world datasets, and fine-tune an LLM to translate NL user requests to their symbolic form, which is sent to the symbolic solver to compute optimal itineraries. Our NL-symbolic translation achieves ~91% exact match in a backtranslation metric (i.e., whether the estimated symbolic form of generated natural language matches the groundtruth), and its returned itineraries have a ratio of 0.979 compared to the optimal cost of the ground truth user request. When evaluated by users, TTG achieves consistently high Net Promoter Scores (NPS) of 35-40% on generated itinerary.

Macroscopic auxiliary asymptotic preserving neural networks for the linear radiative transfer equations

We develop a Macroscopic Auxiliary Asymptotic-Preserving Neural Network (MA-APNN) method to solve the time-dependent linear radiative transfer equations (LRTEs), which have a multi-scale nature and high dimensionality. To achieve this, we utilize the Physics-Informed Neural Networks (PINNs) framework and design a new adaptive exponentially weighted Asymptotic-Preserving (AP) loss function, which incorporates the macroscopic auxiliary equation that is derived from the original transfer equation directly and explicitly contains the information of the diffusion limit equation. Thus, as the scale parameter tends to zero, the loss function gradually transitions from the transport state to the diffusion limit state. In addition, the initial data, boundary conditions, and conservation laws serve as the regularization terms for the loss. We present several numerical examples to demonstrate the effectiveness of MA-APNNs.

Resprompt: Residual Connection Prompting Advances Multi-Step Reasoning in Large Language Models

Chain-of-thought (CoT) prompting, which offers step-by-step problem-solving rationales, has impressively unlocked the reasoning potential of large language models (LLMs). Yet, the standard CoT is less effective in problems demanding multiple reasoning steps. This limitation arises from the complex reasoning process in multi-step problems: later stages often depend on the results of several steps earlier, not just the results of the immediately preceding step. Such complexities suggest the reasoning process is naturally represented as a graph. The almost linear and straightforward structure of CoT prompting, however, struggles to capture this complex reasoning graph. To address this challenge, we propose Residual Connection Prompting (RESPROMPT), a new prompting strategy that advances multi-step reasoning in LLMs. Our key idea is to reconstruct the reasoning graph within prompts. We achieve this by integrating necessary connections-links present in the reasoning graph but missing in the linear CoT flow-into the prompts. Termed "residual connections", these links are pivotal in morphing the linear CoT structure into a graph representation, effectively capturing the complex reasoning graphs inherent in multi-step problems. We evaluate RESPROMPT on six benchmarks across three diverse domains: math, sequential, and commonsense reasoning. For the open-sourced LLaMA family of models, RESPROMPT yields a significant average reasoning accuracy improvement of 12.5% on LLaMA-65B and 6.8% on LLaMA2-70B. Breakdown analysis further highlights RESPROMPT particularly excels in complex multi-step reasoning: for questions demanding at least five reasoning steps, RESPROMPT outperforms the best CoT based benchmarks by a remarkable average improvement of 21.1% on LLaMA-65B and 14.3% on LLaMA2-70B. Through extensive ablation studies and analyses, we pinpoint how to most effectively build residual connections.

On the Equivalence of Graph Convolution and Mixup

This paper investigates the relationship between graph convolution and Mixup techniques. Graph convolution in a graph neural network involves aggregating features from neighboring samples to learn representative features for a specific node or sample. On the other hand, Mixup is a data augmentation technique that generates new examples by averaging features and one-hot labels from multiple samples. One commonality between these techniques is their utilization of information from multiple samples to derive feature representation. This study aims to explore whether a connection exists between these two approaches. Our investigation reveals that, under two mild conditions, graph convolution can be viewed as a specialized form of Mixup that is applied during both the training and testing phases. The two conditions are: 1) \textit{Homophily Relabel} - assigning the target node's label to all its neighbors, and 2) \textit{Test-Time Mixup} - Mixup the feature during the test time. We establish this equivalence mathematically by demonstrating that graph convolution networks (GCN) and simplified graph convolution (SGC) can be expressed as a form of Mixup. We also empirically verify the equivalence by training an MLP using the two conditions to achieve comparable performance.