ProDCARL: Reinforcement Learning-Aligned Diffusion Models for De Novo Antimicrobial Peptide Design

Antimicrobial resistance threatens healthcare sustainability and motivates low-cost computational discovery of antimicrobial peptides (AMPs). De novo peptide generation must optimize antimicrobial activity and safety through low predicted toxicity, but likelihood-trained generators do not enforce these goals explicitly. We introduce ProDCARL, a reinforcement-learning alignment framework that couples a diffusion-based protein generator (EvoDiff OA-DM 38M) with sequence property predictors for AMP activity and peptide toxicity. We fine-tune the diffusion prior on AMP sequences to obtain a domain-aware generator. Top-k policy-gradient updates use classifier-derived rewards plus entropy regularization and early stopping to preserve diversity and reduce reward hacking. In silico experiments show ProDCARL increases the mean predicted AMP score from 0.081 after fine-tuning to 0.178. The joint high-quality hit rate reaches 6.3\% with pAMP $>$0.7 and pTox $<$0.3. ProDCARL maintains high diversity, with $1-$mean pairwise identity equal to 0.929. Qualitative analyses with AlphaFold3 and ProtBERT embeddings suggest candidates show plausible AMP-like structural and semantic characteristics. ProDCARL serves as a candidate generator that narrows experimental search space, and experimental validation remains future work.

Counterfactual Cultural Cues Reduce Medical QA Accuracy in LLMs: Identifier vs Context Effects

Engineering sustainable and equitable healthcare requires medical language models that do not change clinically correct diagnoses when presented with non-decisive cultural information. We introduce a counterfactual benchmark that expands 150 MedQA test items into 1650 variants by inserting culture-related (i) identifier tokens, (ii) contextual cues, or (iii) their combination for three groups (Indigenous Canadian, Middle-Eastern Muslim, Southeast Asian), plus a length-matched neutral control, where a clinician verified that the gold answer remains invariant in all variants. We evaluate GPT-5.2, Llama-3.1-8B, DeepSeek-R1, and MedGemma (4B/27B) under option-only and brief-explanation prompting. Across models, cultural cues significantly affect accuracy (Cochran's Q, $p<10^-14$), with the largest degradation when identifier and context co-occur (up to 3-7 percentage points under option-only prompting), while neutral edits produce smaller, non-systematic changes. A human-validated rubric ($κ=0.76$) applied via an LLM-as-judge shows that more than half of culturally grounded explanations end in an incorrect answer, linking culture-referential reasoning to diagnostic failure. We release prompts and augmentations to support evaluation and mitigation of culturally induced diagnostic errors.

Externally Validated Longitudinal GRU Model for Visit-Level 180-Day Mortality Risk in Metastatic Castration-Resistant Prostate Cancer

Metastatic castration-resistant prostate cancer (mCRPC) is a highly aggressive disease with poor prognosis and heterogeneous treatment response. In this work, we developed and externally validated a visit-level 180-day mortality risk model using longitudinal data from two Phase III cohorts (n=526 and n=640). Only visits with observable 180-day outcomes were labeled; right-censored cases were excluded from analysis. We compared five candidate architectures: Long Short-Term Memory, Gated Recurrent Unit (GRU), Cox Proportional Hazards, Random Survival Forest (RSF), and Logistic Regression. For each dataset, we selected the smallest risk-threshold that achieved an 85% sensitivity floor. The GRU and RSF models showed high discrimination capabilities initially (C-index: 87% for both). In external validation, the GRU obtained a higher calibration (slope: 0.93; intercept: 0.07) and achieved an PR-AUC of 0.87. Clinical impact analysis showed a median time-in-warning of 151.0 days for true positives (59.0 days for false positives) and 18.3 alerts per 100 patient-visits. Given late-stage frailty or cachexia and hemodynamic instability, permutation importance ranked BMI and systolic blood pressure as the strongest associations. These results suggest that longitudinal routine clinical markers can estimate short-horizon mortality risk in mCRPC and support proactive care planning over a multi-month window.

Scaling Public Health Text Annotation: Zero-Shot Learning vs. Crowdsourcing for Improved Efficiency and Labeling Accuracy

Public health researchers are increasingly interested in using social media data to study health-related behaviors, but manually labeling this data can be labor-intensive and costly. This study explores whether zero-shot labeling using large language models (LLMs) can match or surpass conventional crowd-sourced annotation for Twitter posts related to sleep disorders, physical activity, and sedentary behavior. Multiple annotation pipelines were designed to compare labels produced by domain experts, crowd workers, and LLM-driven approaches under varied prompt-engineering strategies. Our findings indicate that LLMs can rival human performance in straightforward classification tasks and significantly reduce labeling time, yet their accuracy diminishes for tasks requiring more nuanced domain knowledge. These results clarify the trade-offs between automated scalability and human expertise, demonstrating conditions under which LLM-based labeling can be efficiently integrated into public health research without undermining label quality.

Detecting Bias and Enhancing Diagnostic Accuracy in Large Language Models for Healthcare

Biased AI-generated medical advice and misdiagnoses can jeopardize patient safety, making the integrity of AI in healthcare more critical than ever. As Large Language Models (LLMs) take on a growing role in medical decision-making, addressing their biases and enhancing their accuracy is key to delivering safe, reliable care. This study addresses these challenges head-on by introducing new resources designed to promote ethical and precise AI in healthcare. We present two datasets: BiasMD, featuring 6,007 question-answer pairs crafted to evaluate and mitigate biases in health-related LLM outputs, and DiseaseMatcher, with 32,000 clinical question-answer pairs spanning 700 diseases, aimed at assessing symptom-based diagnostic accuracy. Using these datasets, we developed the EthiClinician, a fine-tuned model built on the ChatDoctor framework, which outperforms GPT-4 in both ethical reasoning and clinical judgment. By exposing and correcting hidden biases in existing models for healthcare, our work sets a new benchmark for safer, more reliable patient outcomes.

Resprompt: Residual Connection Prompting Advances Multi-Step Reasoning in Large Language Models

Chain-of-thought (CoT) prompting, which offers step-by-step problem-solving rationales, has impressively unlocked the reasoning potential of large language models (LLMs). Yet, the standard CoT is less effective in problems demanding multiple reasoning steps. This limitation arises from the complex reasoning process in multi-step problems: later stages often depend on the results of several steps earlier, not just the results of the immediately preceding step. Such complexities suggest the reasoning process is naturally represented as a graph. The almost linear and straightforward structure of CoT prompting, however, struggles to capture this complex reasoning graph. To address this challenge, we propose Residual Connection Prompting (RESPROMPT), a new prompting strategy that advances multi-step reasoning in LLMs. Our key idea is to reconstruct the reasoning graph within prompts. We achieve this by integrating necessary connections-links present in the reasoning graph but missing in the linear CoT flow-into the prompts. Termed "residual connections", these links are pivotal in morphing the linear CoT structure into a graph representation, effectively capturing the complex reasoning graphs inherent in multi-step problems. We evaluate RESPROMPT on six benchmarks across three diverse domains: math, sequential, and commonsense reasoning. For the open-sourced LLaMA family of models, RESPROMPT yields a significant average reasoning accuracy improvement of 12.5% on LLaMA-65B and 6.8% on LLaMA2-70B. Breakdown analysis further highlights RESPROMPT particularly excels in complex multi-step reasoning: for questions demanding at least five reasoning steps, RESPROMPT outperforms the best CoT based benchmarks by a remarkable average improvement of 21.1% on LLaMA-65B and 14.3% on LLaMA2-70B. Through extensive ablation studies and analyses, we pinpoint how to most effectively build residual connections.

On the Equivalence of Graph Convolution and Mixup

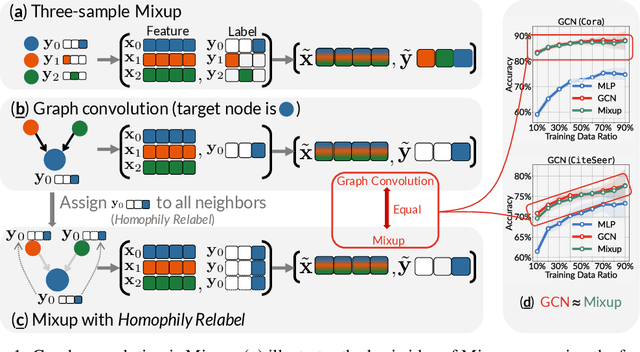
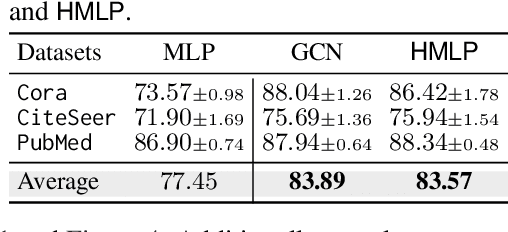
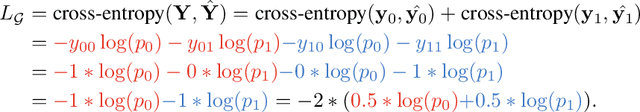
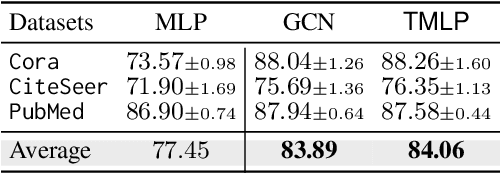
This paper investigates the relationship between graph convolution and Mixup techniques. Graph convolution in a graph neural network involves aggregating features from neighboring samples to learn representative features for a specific node or sample. On the other hand, Mixup is a data augmentation technique that generates new examples by averaging features and one-hot labels from multiple samples. One commonality between these techniques is their utilization of information from multiple samples to derive feature representation. This study aims to explore whether a connection exists between these two approaches. Our investigation reveals that, under two mild conditions, graph convolution can be viewed as a specialized form of Mixup that is applied during both the training and testing phases. The two conditions are: 1) \textit{Homophily Relabel} - assigning the target node's label to all its neighbors, and 2) \textit{Test-Time Mixup} - Mixup the feature during the test time. We establish this equivalence mathematically by demonstrating that graph convolution networks (GCN) and simplified graph convolution (SGC) can be expressed as a form of Mixup. We also empirically verify the equivalence by training an MLP using the two conditions to achieve comparable performance.

Prosody Transfer in Neural Text to Speech Using Global Pitch and Loudness Features

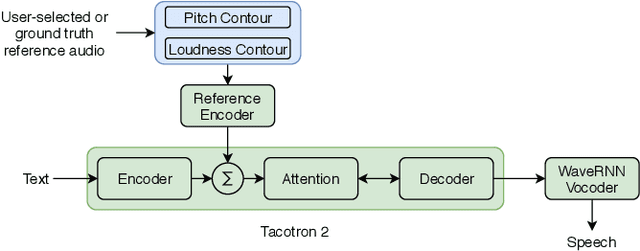
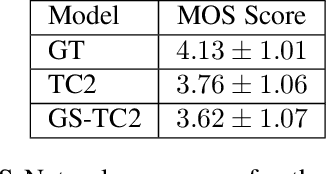
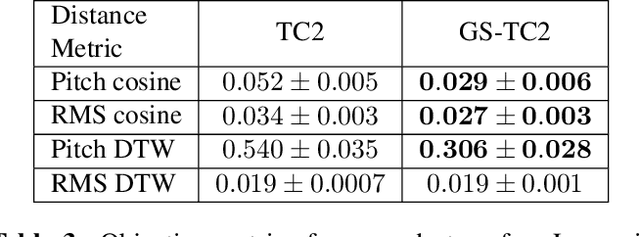
This paper presents a simple yet effective method to achieve prosody transfer from a reference speech signal to synthesized speech. The main idea is to incorporate well-known acoustic correlates of prosody such as pitch and loudness contours of the reference speech into a modern neural text-to-speech (TTS) synthesizer such as Tacotron2 (TC2). More specifically, a small set of acoustic features are extracted from the reference audio and then used to condition a TC2 synthesizer. The trained model is evaluated using subjective listening tests and novel objective evaluations of prosody transfer are proposed. Listening tests show that the synthesized speech is rated as highly natural and that prosody is successfully transferred from the reference speech signal to the synthesized signal.

Learning Mixtures of Separable Dictionaries for Tensor Data: Analysis and Algorithms

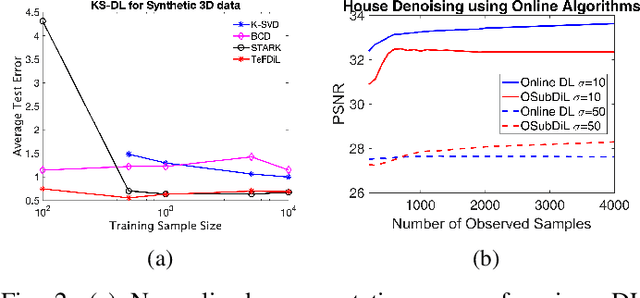
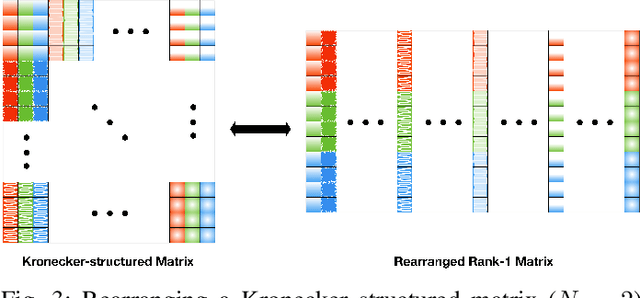
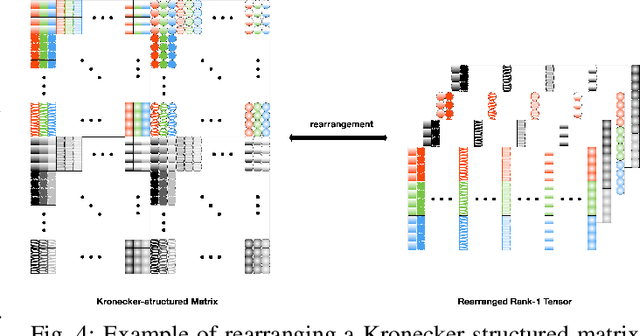
This work addresses the problem of learning sparse representations of tensor data using structured dictionary learning. It proposes learning a mixture of separable dictionaries to better capture the structure of tensor data by generalizing the separable dictionary learning model. Two different approaches for learning mixture of separable dictionaries are explored and sufficient conditions for local identifiability of the underlying dictionary are derived in each case. Moreover, computational algorithms are developed to solve the problem of learning mixture of separable dictionaries in both batch and online settings. Numerical experiments are used to show the usefulness of the proposed model and the efficacy of the developed algorithms.

Identifiability of Kronecker-structured Dictionaries for Tensor Data

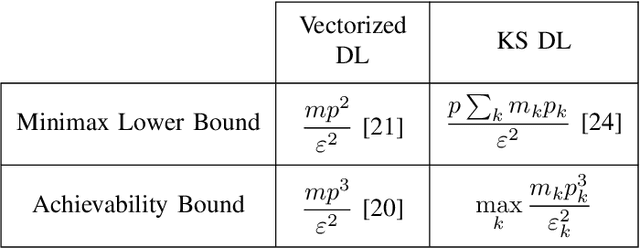
This paper derives sufficient conditions for local recovery of coordinate dictionaries comprising a Kronecker-structured dictionary that is used for representing $K$th-order tensor data. Tensor observations are assumed to be generated from a Kronecker-structured dictionary multiplied by sparse coefficient tensors that follow the separable sparsity model. This work provides sufficient conditions on the underlying coordinate dictionaries, coefficient and noise distributions, and number of samples that guarantee recovery of the individual coordinate dictionaries up to a specified error, as a local minimum of the objective function, with high probability. In particular, the sample complexity to recover $K$ coordinate dictionaries with dimensions $m_k \times p_k$ up to estimation error $\varepsilon_k$ is shown to be $\max_{k \in [K]}\mathcal{O}(m_kp_k^3\varepsilon_k^{-2})$.