Identifiability of Kronecker-structured Dictionaries for Tensor Data
Paper and Code
May 25, 2018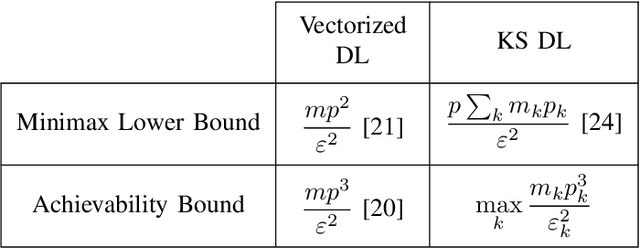
This paper derives sufficient conditions for local recovery of coordinate dictionaries comprising a Kronecker-structured dictionary that is used for representing $K$th-order tensor data. Tensor observations are assumed to be generated from a Kronecker-structured dictionary multiplied by sparse coefficient tensors that follow the separable sparsity model. This work provides sufficient conditions on the underlying coordinate dictionaries, coefficient and noise distributions, and number of samples that guarantee recovery of the individual coordinate dictionaries up to a specified error, as a local minimum of the objective function, with high probability. In particular, the sample complexity to recover $K$ coordinate dictionaries with dimensions $m_k \times p_k$ up to estimation error $\varepsilon_k$ is shown to be $\max_{k \in [K]}\mathcal{O}(m_kp_k^3\varepsilon_k^{-2})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge