Waheed U. Bajwa
DIGing--SGLD: Decentralized and Scalable Langevin Sampling over Time--Varying Networks
Nov 16, 2025Abstract:Sampling from a target distribution induced by training data is central to Bayesian learning, with Stochastic Gradient Langevin Dynamics (SGLD) serving as a key tool for scalable posterior sampling and decentralized variants enabling learning when data are distributed across a network of agents. This paper introduces DIGing-SGLD, a decentralized SGLD algorithm designed for scalable Bayesian learning in multi-agent systems operating over time-varying networks. Existing decentralized SGLD methods are restricted to static network topologies, and many exhibit steady-state sampling bias caused by network effects, even when full batches are used. DIGing-SGLD overcomes these limitations by integrating Langevin-based sampling with the gradient-tracking mechanism of the DIGing algorithm, originally developed for decentralized optimization over time-varying networks, thereby enabling efficient and bias-free sampling without a central coordinator. To our knowledge, we provide the first finite-time non-asymptotic Wasserstein convergence guarantees for decentralized SGLD-based sampling over time-varying networks, with explicit constants. Under standard strong convexity and smoothness assumptions, DIGing-SGLD achieves geometric convergence to an $O(\sqrtη)$ neighborhood of the target distribution, where $η$ is the stepsize, with dependence on the target accuracy matching the best-known rates for centralized and static-network SGLD algorithms using constant stepsize. Numerical experiments on Bayesian linear and logistic regression validate the theoretical results and demonstrate the strong empirical performance of DIGing-SGLD under dynamically evolving network conditions.
RESIST: Resilient Decentralized Learning Using Consensus Gradient Descent
Feb 11, 2025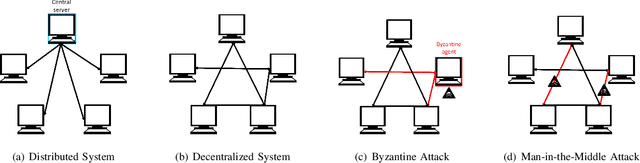
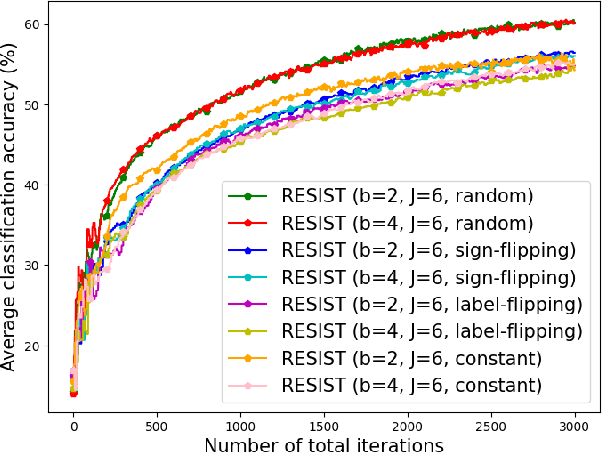
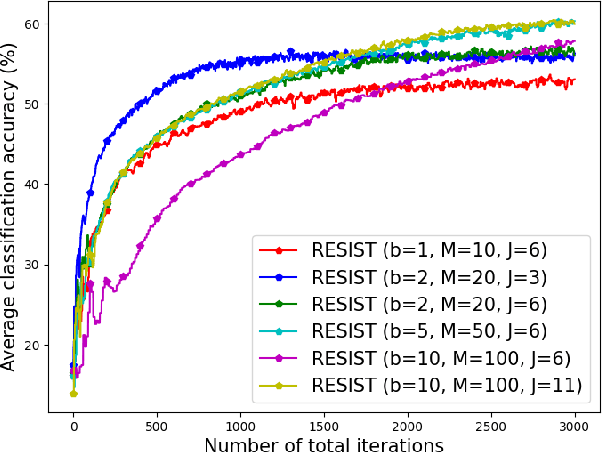
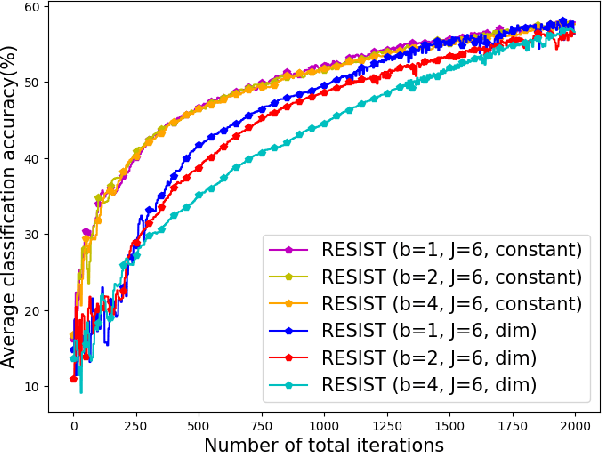
Abstract:Empirical risk minimization (ERM) is a cornerstone of modern machine learning (ML), supported by advances in optimization theory that ensure efficient solutions with provable algorithmic convergence rates, which measure the speed at which optimization algorithms approach a solution, and statistical learning rates, which characterize how well the solution generalizes to unseen data. Privacy, memory, computational, and communications constraints increasingly necessitate data collection, processing, and storage across network-connected devices. In many applications, these networks operate in decentralized settings where a central server cannot be assumed, requiring decentralized ML algorithms that are both efficient and resilient. Decentralized learning, however, faces significant challenges, including an increased attack surface for adversarial interference during decentralized learning processes. This paper focuses on the man-in-the-middle (MITM) attack, which can cause models to deviate significantly from their intended ERM solutions. To address this challenge, we propose RESIST (Resilient dEcentralized learning using conSensus gradIent deScenT), an optimization algorithm designed to be robust against adversarially compromised communication links. RESIST achieves algorithmic and statistical convergence for strongly convex, Polyak-Lojasiewicz, and nonconvex ERM problems. Experimental results demonstrate the robustness and scalability of RESIST for real-world decentralized learning in adversarial environments.
Mitigating Data Injection Attacks on Federated Learning
Dec 04, 2023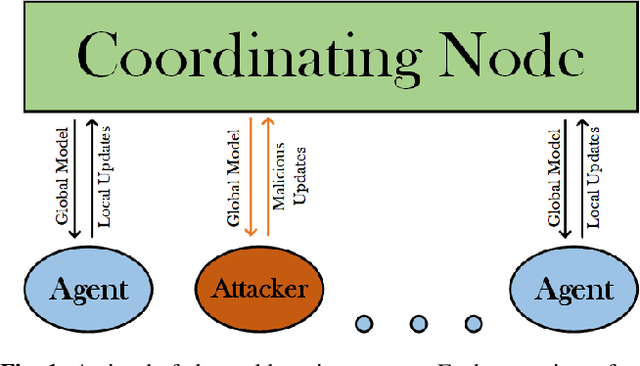
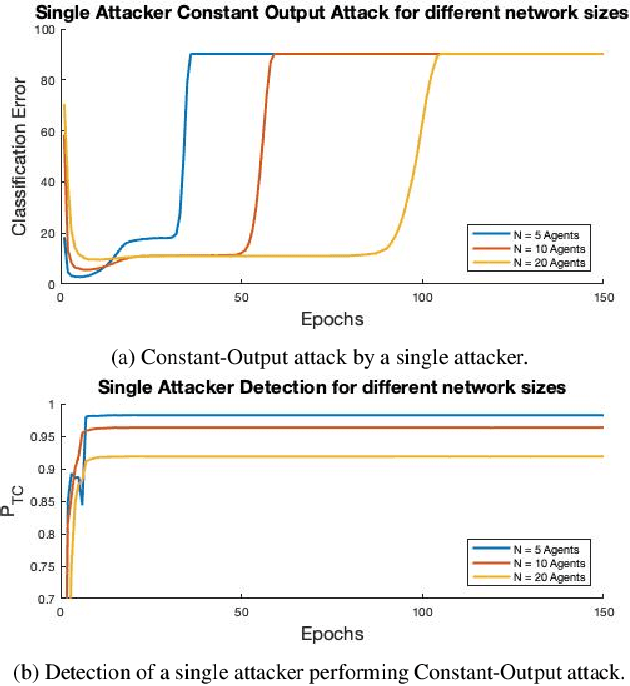
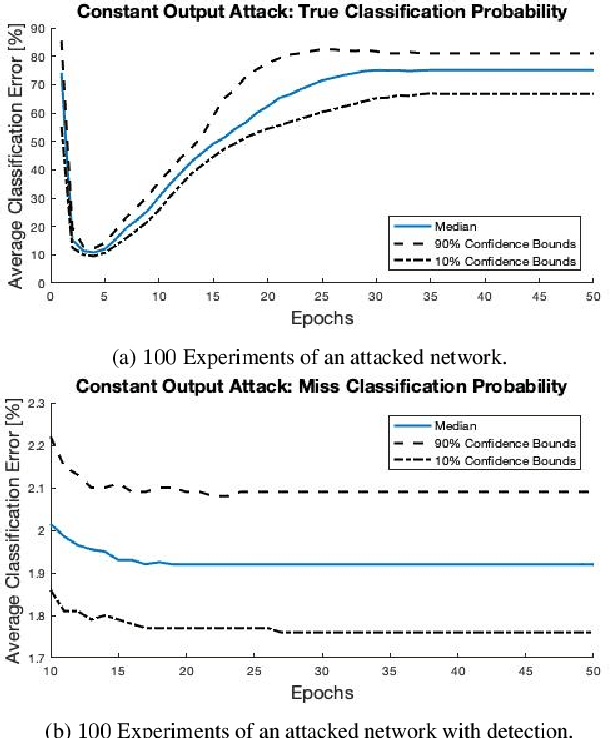
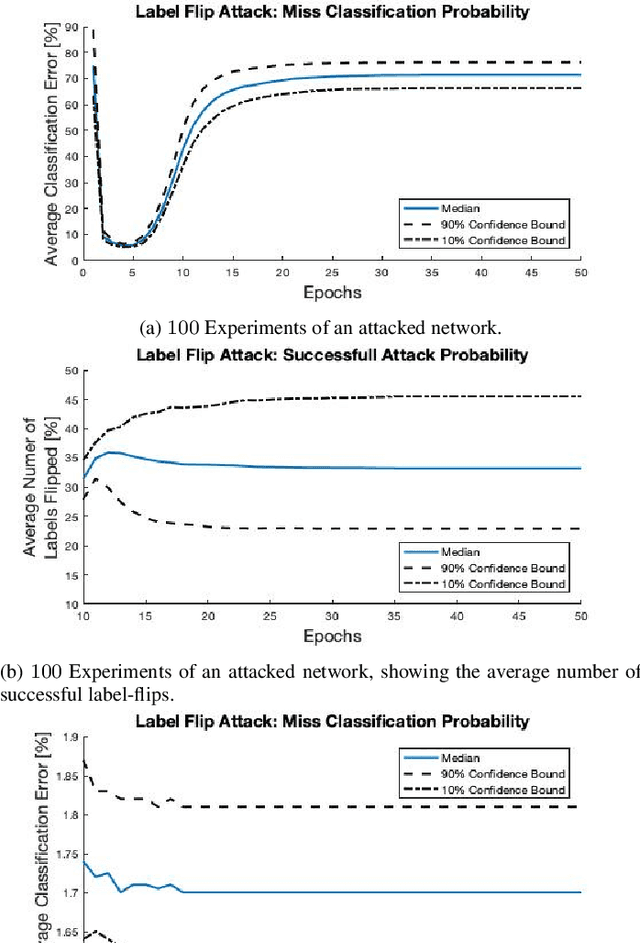
Abstract:Federated learning is a technique that allows multiple entities to collaboratively train models using their data without compromising data privacy. However, despite its advantages, federated learning can be susceptible to false data injection attacks. In these scenarios, a malicious entity with control over specific agents in the network can manipulate the learning process, leading to a suboptimal model. Consequently, addressing these data injection attacks presents a significant research challenge in federated learning systems. In this paper, we propose a novel technique to detect and mitigate data injection attacks on federated learning systems. Our mitigation method is a local scheme, performed during a single instance of training by the coordinating node, allowing the mitigation during the convergence of the algorithm. Whenever an agent is suspected to be an attacker, its data will be ignored for a certain period, this decision will often be re-evaluated. We prove that with probability 1, after a finite time, all attackers will be ignored while the probability of ignoring a trustful agent becomes 0, provided that there is a majority of truthful agents. Simulations show that when the coordinating node detects and isolates all the attackers, the model recovers and converges to the truthful model.
Structured Low-Rank Tensors for Generalized Linear Models
Aug 05, 2023



Abstract:Recent works have shown that imposing tensor structures on the coefficient tensor in regression problems can lead to more reliable parameter estimation and lower sample complexity compared to vector-based methods. This work investigates a new low-rank tensor model, called Low Separation Rank (LSR), in Generalized Linear Model (GLM) problems. The LSR model -- which generalizes the well-known Tucker and CANDECOMP/PARAFAC (CP) models, and is a special case of the Block Tensor Decomposition (BTD) model -- is imposed onto the coefficient tensor in the GLM model. This work proposes a block coordinate descent algorithm for parameter estimation in LSR-structured tensor GLMs. Most importantly, it derives a minimax lower bound on the error threshold on estimating the coefficient tensor in LSR tensor GLM problems. The minimax bound is proportional to the intrinsic degrees of freedom in the LSR tensor GLM problem, suggesting that its sample complexity may be significantly lower than that of vectorized GLMs. This result can also be specialised to lower bound the estimation error in CP and Tucker-structured GLMs. The derived bounds are comparable to tight bounds in the literature for Tucker linear regression, and the tightness of the minimax lower bound is further assessed numerically. Finally, numerical experiments on synthetic datasets demonstrate the efficacy of the proposed LSR tensor model for three regression types (linear, logistic and Poisson). Experiments on a collection of medical imaging datasets demonstrate the usefulness of the LSR model over other tensor models (Tucker and CP) on real, imbalanced data with limited available samples.
* 43 pages; published in Transactions on Machine Learning Research (08/2023)
Accelerated gradient methods for nonconvex optimization: Escape trajectories from strict saddle points and convergence to local minima
Jul 13, 2023



Abstract:This paper considers the problem of understanding the behavior of a general class of accelerated gradient methods on smooth nonconvex functions. Motivated by some recent works that have proposed effective algorithms, based on Polyak's heavy ball method and the Nesterov accelerated gradient method, to achieve convergence to a local minimum of nonconvex functions, this work proposes a broad class of Nesterov-type accelerated methods and puts forth a rigorous study of these methods encompassing the escape from saddle-points and convergence to local minima through a both asymptotic and a non-asymptotic analysis. In the asymptotic regime, this paper answers an open question of whether Nesterov's accelerated gradient method (NAG) with variable momentum parameter avoids strict saddle points almost surely. This work also develops two metrics of asymptotic rate of convergence and divergence, and evaluates these two metrics for several popular standard accelerated methods such as the NAG, and Nesterov's accelerated gradient with constant momentum (NCM) near strict saddle points. In the local regime, this work provides an analysis that leads to the "linear" exit time estimates from strict saddle neighborhoods for trajectories of these accelerated methods as well the necessary conditions for the existence of such trajectories. Finally, this work studies a sub-class of accelerated methods that can converge in convex neighborhoods of nonconvex functions with a near optimal rate to a local minima and at the same time this sub-class offers superior saddle-escape behavior compared to that of NAG.
Space-Time Digitally-Coded Metamaterial Antenna Enabled Directional Modulation for Physical Layer Security
Nov 16, 2022Abstract:Developing low-cost and scalable security solutions is vital to the advent of future large-scale wireless networks. Traditional cryptographic methods fail to meet the low-latency and scalability requirements of these networks due to their computational and key management complexity. On the other hand, physical layer (PHY) security has been put forth as a cost-effective alternative to cryptographic mechanisms that can circumvent the need for explicit key exchange between communication devices, owing to the fact that PHY security relies on the physics of the signal transmission for providing security. In this work, we propose a space-time-modulated digitally-coded metamaterial (MTM) leaky wave antenna (LWA) that can enable PHY security by achieving the functionalities of directional modulation (DM). From the theoretical perspective, we first show how the proposed space-time MTM antenna architecture can achieve DM through both the spatial and spectral manipulation of the orthogonal frequency division multiplexing (OFDM) signal received by a user equipment (UE). Simulation results are then provided as proof-of-principle, demonstrating the applicability of our approach for achieving DM in various communication settings. To further validate our simulation results, we realize a prototype of the proposed architecture controlled by a field-programmable gate array (FPGA), which achieves DM via an optimized coding sequence carried out by the branch-and-bound algorithm corresponding to the states of the MTM LWA's unit cells. Experimental results confirm the theory behind the space-time-modulated MTM LWA in achieving DM, which is observed via both the spectral harmonic patterns and bit error rate (BER) measurements.
Domain-informed neural networks for interaction localization within astroparticle experiments
Dec 15, 2021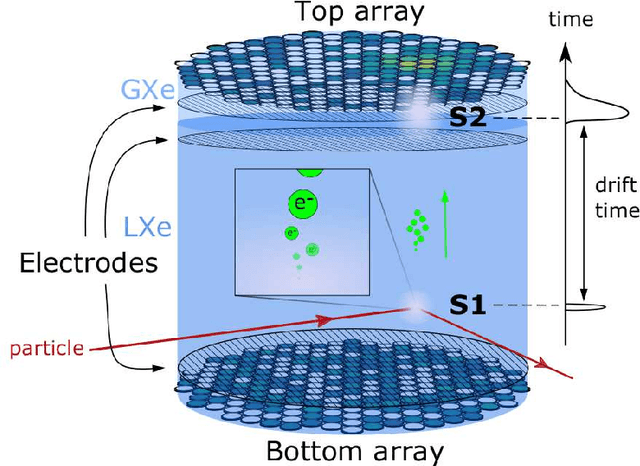
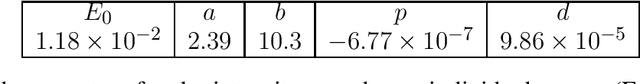
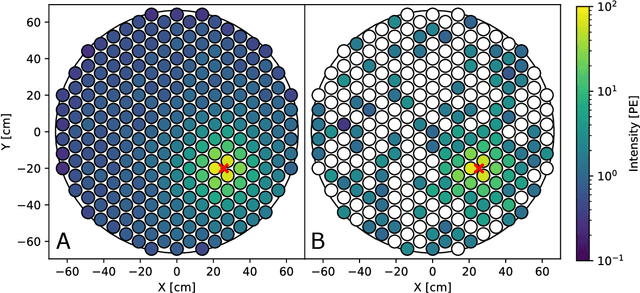
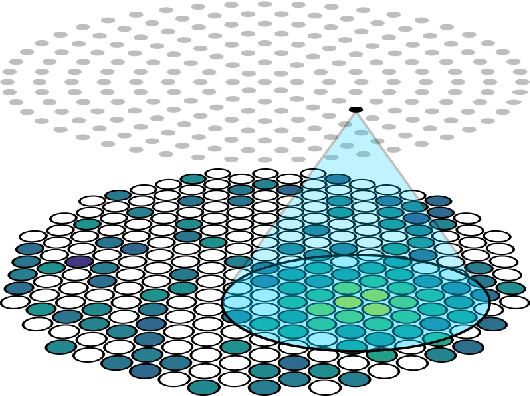
Abstract:This work proposes a domain-informed neural network architecture for experimental particle physics, using particle interaction localization with the time-projection chamber (TPC) technology for dark matter research as an example application. A key feature of the signals generated within the TPC is that they allow localization of particle interactions through a process called reconstruction. While multilayer perceptrons (MLPs) have emerged as a leading contender for reconstruction in TPCs, such a black-box approach does not reflect prior knowledge of the underlying scientific processes. This paper looks anew at neural network-based interaction localization and encodes prior detector knowledge, in terms of both signal characteristics and detector geometry, into the feature encoding and the output layers of a multilayer neural network. The resulting Domain-informed Neural Network (DiNN limits the receptive fields of the neurons in the initial feature encoding layers in order to account for the spatially localized nature of the signals produced within the TPC. This aspect of the DiNN, which has similarities with the emerging area of graph neural networks in that the neurons in the initial layers only connect to a handful of neurons in their succeeding layer, significantly reduces the number of parameters in the network in comparison to an MLP. In addition, in order to account for the detector geometry, the output layers of the network are modified using two geometric transformations to ensure the DiNN produces localizations within the interior of the detector. The end result is a neural network architecture that has 60% fewer parameters than an MLP, but that still achieves similar localization performance and provides a path to future architectural developments with improved performance because of their ability to encode additional domain knowledge into the architecture.
A Guide to Reproducible Research in Signal Processing and Machine Learning
Aug 27, 2021

Abstract:Reproducibility is a growing problem that has been extensively studied among computational researchers and within the signal processing and machine learning research community. However, with the changing landscape of signal processing and machine learning research come new obstacles and unseen challenges in creating reproducible experiments. Due to these new challenges most experiments have become difficult, if not impossible, to be reproduced by an independent researcher. In 2016 a survey conducted by the journal Nature found that 50% of researchers were unable to reproduce their own experiments. While the issue of reproducibility has been discussed in the literature and specifically within the signal processing community, it is still unclear to most researchers what are the best practices to ensure reproducibility without impinging on their primary responsibility of conducting research. We feel that although researchers understand the importance of making experiments reproducible, the lack of a clear set of standards and tools makes it difficult to incorporate good reproducibility practices in most labs. It is in this regard that we aim to present signal processing researchers with a set of practical tools and strategies that can help mitigate many of the obstacles to producing reproducible computational experiments.
FAST-PCA: A Fast and Exact Algorithm for Distributed Principal Component Analysis
Aug 27, 2021


Abstract:Principal Component Analysis (PCA) is a fundamental data preprocessing tool in the world of machine learning. While PCA is often reduced to dimension reduction, the purpose of PCA is actually two-fold: dimension reduction and feature learning. Furthermore, the enormity of the dimensions and sample size in the modern day datasets have rendered the centralized PCA solutions unusable. In that vein, this paper reconsiders the problem of PCA when data samples are distributed across nodes in an arbitrarily connected network. While a few solutions for distributed PCA exist those either overlook the feature learning part of the purpose, have communication overhead making them inefficient and/or lack exact convergence guarantees. To combat these aforementioned issues, this paper proposes a distributed PCA algorithm called FAST-PCA (Fast and exAct diSTributed PCA). The proposed algorithm is efficient in terms of communication and can be proved to converge linearly and exactly to the principal components that lead to dimension reduction as well as uncorrelated features. Our claims are further supported by experimental results.
A hybrid model-based and learning-based approach for classification using limited number of training samples
Jun 25, 2021



Abstract:The fundamental task of classification given a limited number of training data samples is considered for physical systems with known parametric statistical models. The standalone learning-based and statistical model-based classifiers face major challenges towards the fulfillment of the classification task using a small training set. Specifically, classifiers that solely rely on the physics-based statistical models usually suffer from their inability to properly tune the underlying unobservable parameters, which leads to a mismatched representation of the system's behaviors. Learning-based classifiers, on the other hand, typically rely on a large number of training data from the underlying physical process, which might not be feasible in most practical scenarios. In this paper, a hybrid classification method -- termed HyPhyLearn -- is proposed that exploits both the physics-based statistical models and the learning-based classifiers. The proposed solution is based on the conjecture that HyPhyLearn would alleviate the challenges associated with the individual approaches of learning-based and statistical model-based classifiers by fusing their respective strengths. The proposed hybrid approach first estimates the unobservable model parameters using the available (suboptimal) statistical estimation procedures, and subsequently use the physics-based statistical models to generate synthetic data. Then, the training data samples are incorporated with the synthetic data in a learning-based classifier that is based on domain-adversarial training of neural networks. Specifically, in order to address the mismatch problem, the classifier learns a mapping from the training data and the synthetic data to a common feature space. Simultaneously, the classifier is trained to find discriminative features within this space in order to fulfill the classification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge