Rishabh Dixit
RESIST: Resilient Decentralized Learning Using Consensus Gradient Descent
Feb 11, 2025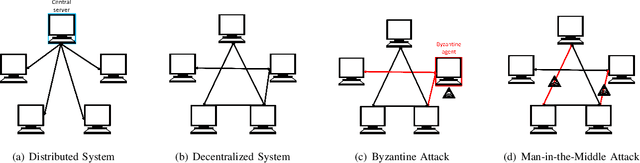
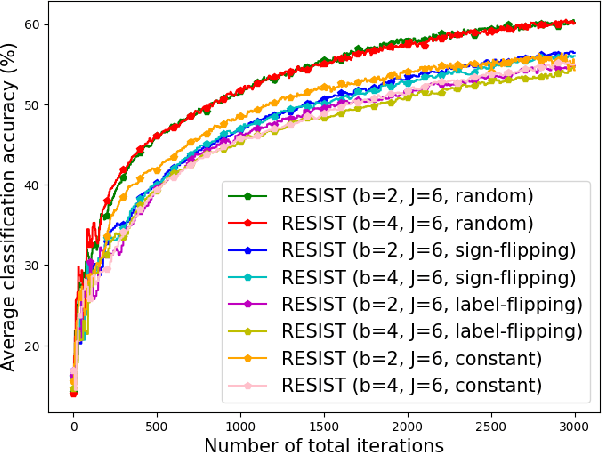
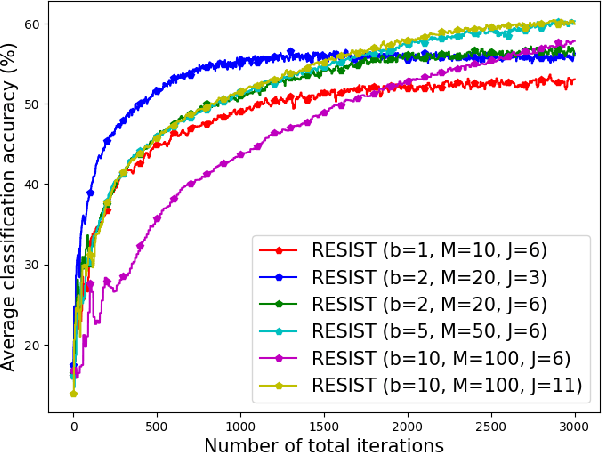
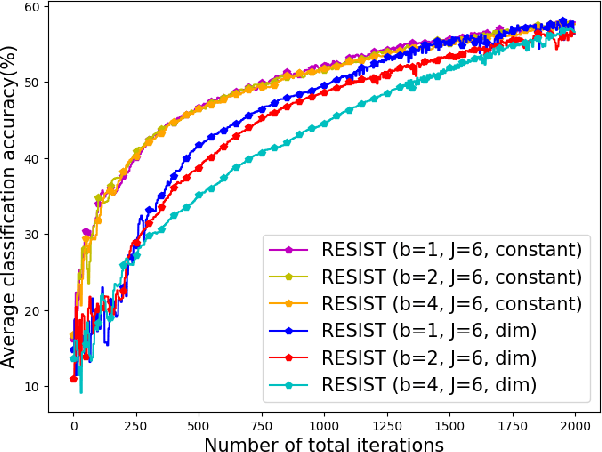
Abstract:Empirical risk minimization (ERM) is a cornerstone of modern machine learning (ML), supported by advances in optimization theory that ensure efficient solutions with provable algorithmic convergence rates, which measure the speed at which optimization algorithms approach a solution, and statistical learning rates, which characterize how well the solution generalizes to unseen data. Privacy, memory, computational, and communications constraints increasingly necessitate data collection, processing, and storage across network-connected devices. In many applications, these networks operate in decentralized settings where a central server cannot be assumed, requiring decentralized ML algorithms that are both efficient and resilient. Decentralized learning, however, faces significant challenges, including an increased attack surface for adversarial interference during decentralized learning processes. This paper focuses on the man-in-the-middle (MITM) attack, which can cause models to deviate significantly from their intended ERM solutions. To address this challenge, we propose RESIST (Resilient dEcentralized learning using conSensus gradIent deScenT), an optimization algorithm designed to be robust against adversarially compromised communication links. RESIST achieves algorithmic and statistical convergence for strongly convex, Polyak-Lojasiewicz, and nonconvex ERM problems. Experimental results demonstrate the robustness and scalability of RESIST for real-world decentralized learning in adversarial environments.
Accelerated gradient methods for nonconvex optimization: Escape trajectories from strict saddle points and convergence to local minima
Jul 13, 2023



Abstract:This paper considers the problem of understanding the behavior of a general class of accelerated gradient methods on smooth nonconvex functions. Motivated by some recent works that have proposed effective algorithms, based on Polyak's heavy ball method and the Nesterov accelerated gradient method, to achieve convergence to a local minimum of nonconvex functions, this work proposes a broad class of Nesterov-type accelerated methods and puts forth a rigorous study of these methods encompassing the escape from saddle-points and convergence to local minima through a both asymptotic and a non-asymptotic analysis. In the asymptotic regime, this paper answers an open question of whether Nesterov's accelerated gradient method (NAG) with variable momentum parameter avoids strict saddle points almost surely. This work also develops two metrics of asymptotic rate of convergence and divergence, and evaluates these two metrics for several popular standard accelerated methods such as the NAG, and Nesterov's accelerated gradient with constant momentum (NCM) near strict saddle points. In the local regime, this work provides an analysis that leads to the "linear" exit time estimates from strict saddle neighborhoods for trajectories of these accelerated methods as well the necessary conditions for the existence of such trajectories. Finally, this work studies a sub-class of accelerated methods that can converge in convex neighborhoods of nonconvex functions with a near optimal rate to a local minima and at the same time this sub-class offers superior saddle-escape behavior compared to that of NAG.
Boundary Conditions for Linear Exit Time Gradient Trajectories Around Saddle Points: Analysis and Algorithm
Jan 07, 2021

Abstract:Gradient-related first-order methods have become the workhorse of large-scale numerical optimization problems. Many of these problems involve nonconvex objective functions with multiple saddle points, which necessitates an understanding of the behavior of discrete trajectories of first-order methods within the geometrical landscape of these functions. This paper concerns convergence of first-order discrete methods to a local minimum of nonconvex optimization problems that comprise strict saddle points within the geometrical landscape. To this end, it focuses on analysis of discrete gradient trajectories around saddle neighborhoods, derives sufficient conditions under which these trajectories can escape strict-saddle neighborhoods in linear time, explores the contractive and expansive dynamics of these trajectories in neighborhoods of strict-saddle points that are characterized by gradients of moderate magnitude, characterizes the non-curving nature of these trajectories, and highlights the inability of these trajectories to re-enter the neighborhoods around strict-saddle points after exiting them. Based on these insights and analyses, the paper then proposes a simple variant of the vanilla gradient descent algorithm, termed Curvature Conditioned Regularized Gradient Descent (CCRGD) algorithm, which utilizes a check for an initial boundary condition to ensure its trajectories can escape strict-saddle neighborhoods in linear time. Convergence analysis of the CCRGD algorithm, which includes its rate of convergence to a local minimum within a geometrical landscape that has a maximum number of strict-saddle points, is also presented in the paper. Numerical experiments are then provided on a test function as well as a low-rank matrix factorization problem to evaluate the efficacy of the proposed algorithm.
Exit Time Analysis for Approximations of Gradient Descent Trajectories Around Saddle Points
Jun 01, 2020



Abstract:This paper considers the problem of understanding the exit time for trajectories of gradient-related first-order methods from saddle neighborhoods under some initial boundary conditions. Given the `flat' geometry around saddle points, first-order methods can struggle in escaping these regions in a fast manner due to the small magnitudes of gradients encountered. In particular, while it is known that gradient-related first-order methods escape strict-saddle neighborhoods, existing literature does not explicitly leverage the local geometry around saddle points in order to control behavior of gradient trajectories. It is in this context that this paper puts forth a rigorous geometric analysis of the gradient-descent method around strict-saddle neighborhoods using matrix perturbation theory. In doing so, it provides a key result that can be used to generate an approximate gradient trajectory for any given initial conditions. In addition, the analysis leads to a linear exit-time solution for gradient-descent method under certain necessary initial conditions for a class of strict-saddle functions.
Online Learning over Dynamic Graphs via Distributed Proximal Gradient Algorithm
May 16, 2019



Abstract:We consider the problem of tracking the minimum of a time-varying convex optimization problem over a dynamic graph. Motivated by target tracking and parameter estimation problems in intermittently connected robotic and sensor networks, the goal is to design a distributed algorithm capable of handling non-differentiable regularization penalties. The proposed proximal online gradient descent algorithm is built to run in a fully decentralized manner and utilizes consensus updates over possibly disconnected graphs. The performance of the proposed algorithm is analyzed by developing bounds on its dynamic regret in terms of the cumulative path length of the time-varying optimum. It is shown that as compared to the centralized case, the dynamic regret incurred by the proposed algorithm over $T$ time slots is worse by a factor of $\log(T)$ only, despite the disconnected and time-varying network topology. The empirical performance of the proposed algorithm is tested on the distributed dynamic sparse recovery problem, where it is shown to incur a dynamic regret that is close to that of the centralized algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge