RESIST: Resilient Decentralized Learning Using Consensus Gradient Descent
Paper and Code
Feb 11, 2025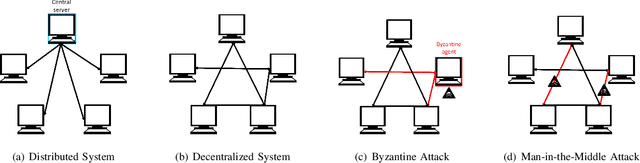
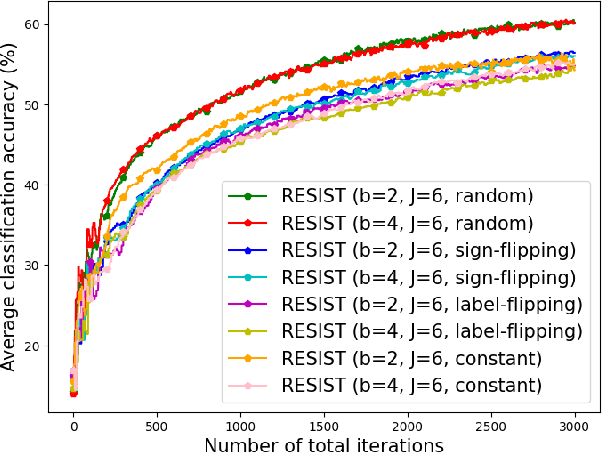
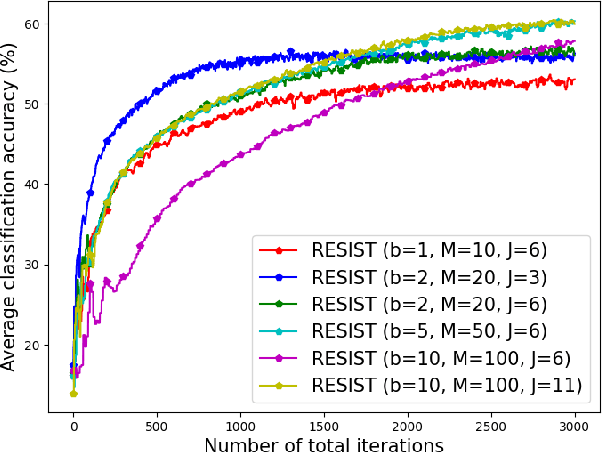
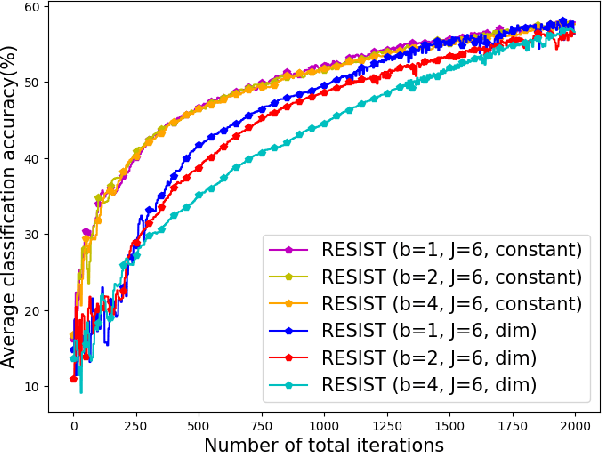
Empirical risk minimization (ERM) is a cornerstone of modern machine learning (ML), supported by advances in optimization theory that ensure efficient solutions with provable algorithmic convergence rates, which measure the speed at which optimization algorithms approach a solution, and statistical learning rates, which characterize how well the solution generalizes to unseen data. Privacy, memory, computational, and communications constraints increasingly necessitate data collection, processing, and storage across network-connected devices. In many applications, these networks operate in decentralized settings where a central server cannot be assumed, requiring decentralized ML algorithms that are both efficient and resilient. Decentralized learning, however, faces significant challenges, including an increased attack surface for adversarial interference during decentralized learning processes. This paper focuses on the man-in-the-middle (MITM) attack, which can cause models to deviate significantly from their intended ERM solutions. To address this challenge, we propose RESIST (Resilient dEcentralized learning using conSensus gradIent deScenT), an optimization algorithm designed to be robust against adversarially compromised communication links. RESIST achieves algorithmic and statistical convergence for strongly convex, Polyak-Lojasiewicz, and nonconvex ERM problems. Experimental results demonstrate the robustness and scalability of RESIST for real-world decentralized learning in adversarial environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge