Ketan Rajawat
Indian Institute of Technology Kanpur
Communication and Energy-Aware Multi-UAV Coverage Path Planning for Networked Operations
Nov 05, 2024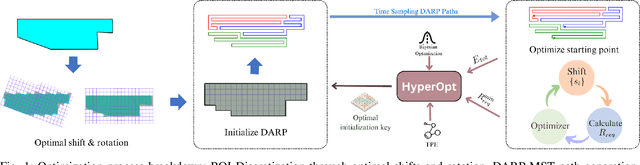
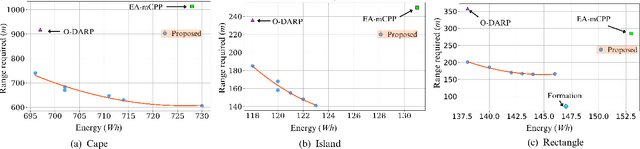


Abstract:This paper presents a communication and energy-aware Multi-UAV Coverage Path Planning (mCPP) method for scenarios requiring continuous inter-UAV communication, such as cooperative search and rescue and surveillance missions. Unlike existing mCPP solutions that focus on energy, time, or coverage efficiency, our approach generates coverage paths that require minimal the communication range to maintain inter-UAV connectivity while also optimizing energy consumption. The mCPP problem is formulated as a multi-objective optimization task, aiming to minimize both the communication range requirement and energy consumption. Our approach significantly reduces the communication range needed for maintaining connectivity while ensuring energy efficiency, outperforming state-of-the-art methods. Its effectiveness is validated through simulations on complex and arbitrary shaped regions of interests, including scenarios with no-fly zones. Additionally, real-world experiment demonstrate its high accuracy, achieving 99\% consistency between the estimated and actual communication range required during a multi-UAV coverage mission involving three UAVs.
UNet: A Generic and Reliable Multi-UAV Communication and Networking Architecture for Heterogeneous Applications
Nov 05, 2024



Abstract:The rapid growth of UAV applications necessitates a robust communication and networking architecture capable of addressing the diverse requirements of various applications concurrently, rather than relying on application-specific solutions. This paper proposes a generic and reliable multi-UAV communication and networking architecture designed to support the varying demands of heterogeneous applications, including short-range and long-range communication, star and mesh topologies, different data rates, and multiple wireless standards. Our architecture accommodates both adhoc and infrastructure networks, ensuring seamless connectivity throughout the network. Additionally, we present the design of a multi-protocol UAV gateway that enables interoperability among various communication protocols. Furthermore, we introduce a data processing and service layer framework with a graphical user interface of a ground control station that facilitates remote control and monitoring from any location at any time. We practically implemented the proposed architecture and evaluated its performance using different metrics, demonstrating its effectiveness.
Analysis of Decentralized Stochastic Successive Convex Approximation for composite non-convex problems
May 11, 2024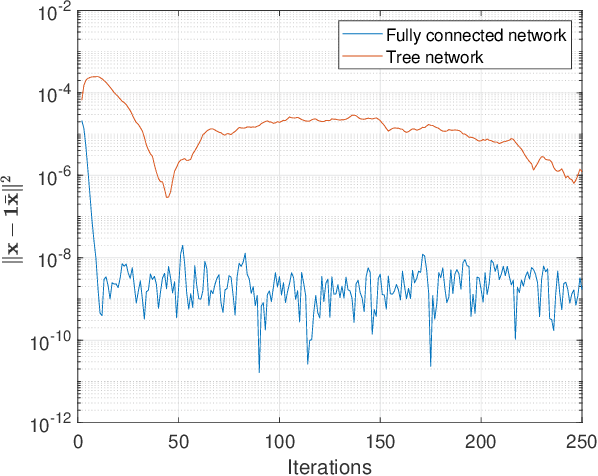
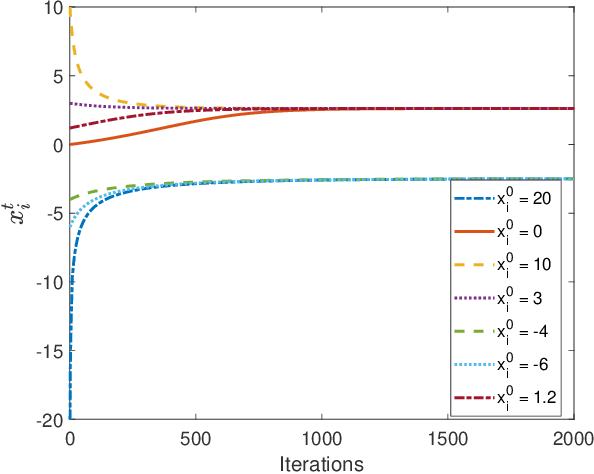
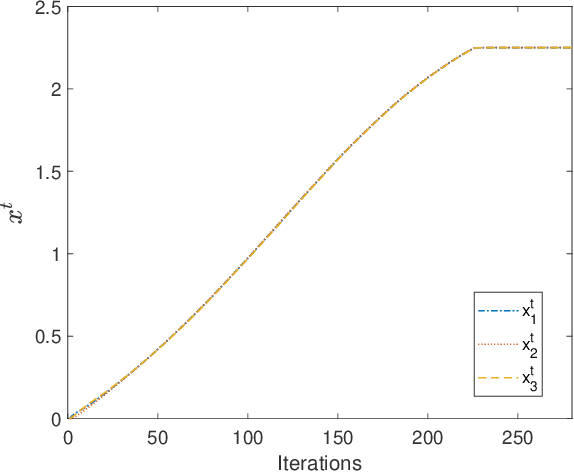
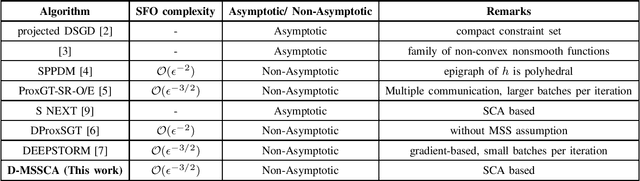
Abstract:Successive Convex approximation (SCA) methods have shown to improve the empirical convergence of non-convex optimization problems over proximal gradient-based methods. In decentralized optimization, which aims to optimize a global function using only local information, the SCA framework has been successfully applied to achieve improved convergence. Still, the stochastic first order (SFO) complexity of decentralized SCA algorithms has remained understudied. While non-asymptotic convergence analysis has been studied for decentralized deterministic settings, its stochastic counterpart has only been shown to converge asymptotically. We have analyzed a novel accelerated variant of the decentralized stochastic SCA that minimizes the sum of non-convex (possibly smooth) and convex (possibly non-smooth) cost functions. The algorithm viz. Decentralized Momentum-based Stochastic SCA (D-MSSCA), iteratively solves a series of strongly convex subproblems at each node using one sample at each iteration. The key step in non-asymptotic analysis involves proving that the average output state vector moves in the descent direction of the global function. This descent allows us to obtain a bound on average \textit{iterate progress} and \emph{mean-squared stationary gap}. The recursive momentum-based updates at each node contribute to achieving stochastic first order (SFO) complexity of O(\epsilon^{-3/2}) provided that the step sizes are smaller than the given upper bounds. Even with one sample used at each iteration and a non-adaptive step size, the rate is at par with the SFO complexity of decentralized state-of-the-art gradient-based algorithms. The rate also matches the lower bound for the centralized, unconstrained optimization problems. Through a synthetic example, the applicability of D-MSSCA is demonstrated.
Constrained Stochastic Recursive Momentum Successive Convex Approximation
Apr 17, 2024



Abstract:We consider stochastic optimization problems with functional constraints. If the objective and constraint functions are not convex, the classical stochastic approximation algorithms such as the proximal stochastic gradient descent do not lead to efficient algorithms. In this work, we put forth an accelerated SCA algorithm that utilizes the recursive momentum-based acceleration which is widely used in the unconstrained setting. Remarkably, the proposed algorithm also achieves the optimal SFO complexity, at par with that achieved by state-of-the-art (unconstrained) stochastic optimization algorithms and match the SFO-complexity lower bound for minimization of general smooth functions. At each iteration, the proposed algorithm entails constructing convex surrogates of the objective and the constraint functions, and solving the resulting convex optimization problem. A recursive update rule is employed to track the gradient of the objective function, and contributes to achieving faster convergence and improved SFO complexity. A key ingredient of the proof is a new parameterized version of the standard Mangasarian-Fromowitz Constraints Qualification, that allows us to bound the dual variables and hence establish that the iterates approach an $\epsilon$-stationary point. We also detail a obstacle-avoiding trajectory optimization problem that can be solved using the proposed algorithm, and show that its performance is superior to that of the existing algorithms. The performance of the proposed algorithm is also compared against that of a specialized sparse classification algorithm on a binary classification problem.
Optimized Gradient Tracking for Decentralized Online Learning
Jun 10, 2023Abstract:This work considers the problem of decentralized online learning, where the goal is to track the optimum of the sum of time-varying functions, distributed across several nodes in a network. The local availability of the functions and their gradients necessitates coordination and consensus among the nodes. We put forth the Generalized Gradient Tracking (GGT) framework that unifies a number of existing approaches, including the state-of-the-art ones. The performance of the proposed GGT algorithm is theoretically analyzed using a novel semidefinite programming-based analysis that yields the desired regret bounds under very general conditions and without requiring the gradient boundedness assumption. The results are applicable to the special cases of GGT, which include various state-of-the-art algorithms as well as new dynamic versions of various classical decentralized algorithms. To further minimize the regret, we consider a condensed version of GGT with only four free parameters. A procedure for offline tuning of these parameters using only the problem parameters is also detailed. The resulting optimized GGT (oGGT) algorithm not only achieves improved dynamic regret bounds, but also outperforms all state-of-the-art algorithms on both synthetic and real-world datasets.
Sharpened Lazy Incremental Quasi-Newton Method
May 26, 2023Abstract:We consider the finite sum minimization of $n$ strongly convex and smooth functions with Lipschitz continuous Hessians in $d$ dimensions. In many applications where such problems arise, including maximum likelihood estimation, empirical risk minimization, and unsupervised learning, the number of observations $n$ is large, and it becomes necessary to use incremental or stochastic algorithms whose per-iteration complexity is independent of $n$. Of these, the incremental/stochastic variants of the Newton method exhibit superlinear convergence, but incur a per-iteration complexity of $O(d^3)$, which may be prohibitive in large-scale settings. On the other hand, the incremental Quasi-Newton method incurs a per-iteration complexity of $O(d^2)$ but its superlinear convergence rate has only been characterized asymptotically. This work puts forth the Sharpened Lazy Incremental Quasi-Newton (SLIQN) method that achieves the best of both worlds: an explicit superlinear convergence rate with a per-iteration complexity of $O(d^2)$. Building upon the recently proposed Sharpened Quasi-Newton method, the proposed incremental variant incorporates a hybrid update strategy incorporating both classic and greedy BFGS updates. The proposed lazy update rule distributes the computational complexity between the iterations, so as to enable a per-iteration complexity of $O(d^2)$. Numerical tests demonstrate the superiority of SLIQN over all other incremental and stochastic Quasi-Newton variants.
Low-complexity subspace-descent over symmetric positive definite manifold
May 03, 2023Abstract:This work puts forth low-complexity Riemannian subspace descent algorithms for the minimization of functions over the symmetric positive definite (SPD) manifold. Different from the existing Riemannian gradient descent variants, the proposed approach utilizes carefully chosen subspaces that allow the update to be written as a product of the Cholesky factor of the iterate and a sparse matrix. The resulting updates avoid the costly matrix operations like matrix exponentiation and dense matrix multiplication, which are generally required in almost all other Riemannian optimization algorithms on SPD manifold. We further identify a broad class of functions, arising in diverse applications, such as kernel matrix learning, covariance estimation of Gaussian distributions, maximum likelihood parameter estimation of elliptically contoured distributions, and parameter estimation in Gaussian mixture model problems, over which the Riemannian gradients can be calculated efficiently. The proposed uni-directional and multi-directional Riemannian subspace descent variants incur per-iteration complexities of $\mathcal{O}(n)$ and $\mathcal{O}(n^2)$ respectively, as compared to the $\mathcal{O}(n^3)$ or higher complexity incurred by all existing Riemannian gradient descent variants. The superior runtime and low per-iteration complexity of the proposed algorithms is also demonstrated via numerical tests on large-scale covariance estimation problems.
FedNew: A Communication-Efficient and Privacy-Preserving Newton-Type Method for Federated Learning
Jun 17, 2022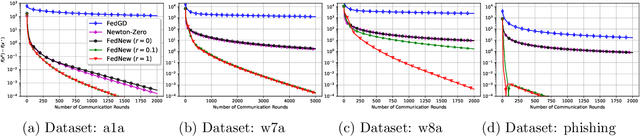
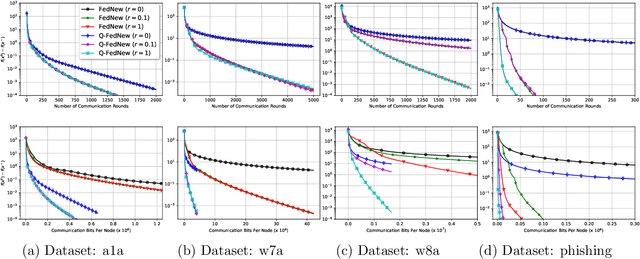
Abstract:Newton-type methods are popular in federated learning due to their fast convergence. Still, they suffer from two main issues, namely: low communication efficiency and low privacy due to the requirement of sending Hessian information from clients to parameter server (PS). In this work, we introduced a novel framework called FedNew in which there is no need to transmit Hessian information from clients to PS, hence resolving the bottleneck to improve communication efficiency. In addition, FedNew hides the gradient information and results in a privacy-preserving approach compared to the existing state-of-the-art. The core novel idea in FedNew is to introduce a two level framework, and alternate between updating the inverse Hessian-gradient product using only one alternating direction method of multipliers (ADMM) step and then performing the global model update using Newton's method. Though only one ADMM pass is used to approximate the inverse Hessian-gradient product at each iteration, we develop a novel theoretical approach to show the converging behavior of FedNew for convex problems. Additionally, a significant reduction in communication overhead is achieved by utilizing stochastic quantization. Numerical results using real datasets show the superiority of FedNew compared to existing methods in terms of communication costs.
Variational Bayesian Filtering with Subspace Information for Extreme Spatio-Temporal Matrix Completion
Jan 20, 2022Abstract:Missing data is a common problem in real-world sensor data collection. The performance of various approaches to impute data degrade rapidly in the extreme scenarios of low data sampling and noisy sampling, a case present in many real-world problems in the field of traffic sensing and environment monitoring, etc. However, jointly exploiting the spatiotemporal and periodic structure, which is generally not captured by classical matrix completion approaches, can improve the imputation performance of sensor data in such real-world conditions. We present a Bayesian approach towards spatiotemporal matrix completion wherein we estimate the underlying temporarily varying subspace using a Variational Bayesian technique. We jointly couple the low-rank matrix completion with the state space autoregressive framework along with a penalty function on the slowly varying subspace to model the temporal and periodic evolution in the data. A major advantage of our method is that a critical parameter like the rank of the model is automatically tuned using the automatic relevance determination (ARD) approach, unlike most matrix/tensor completion techniques. We also propose a robust version of the above formulation, which improves the performance of imputation in the presence of outliers. We evaluate the proposed Variational Bayesian Filtering with Subspace Information (VBFSI) method to impute matrices in real-world traffic and air pollution data. Simulation results demonstrate that the proposed method outperforms the recent state-of-the-art methods and provides a sufficiently accurate imputation for different sampling rates. In particular, we demonstrate that fusing the subspace evolution over days can improve the imputation performance with even 15% of the data sampling.
Projection-Free Algorithm for Stochastic Bi-level Optimization
Oct 22, 2021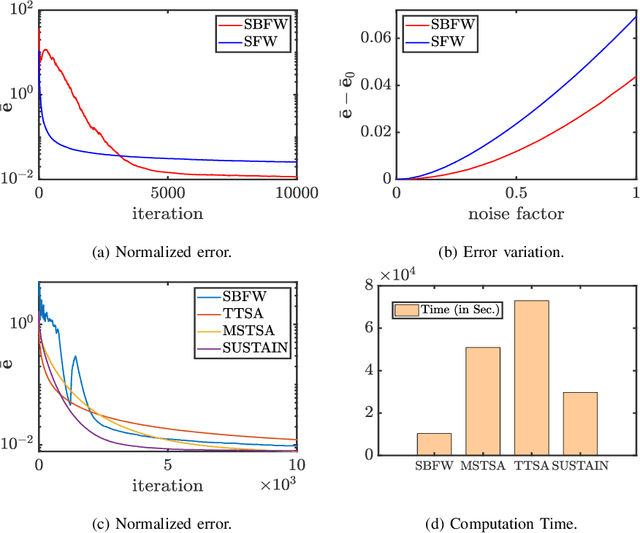
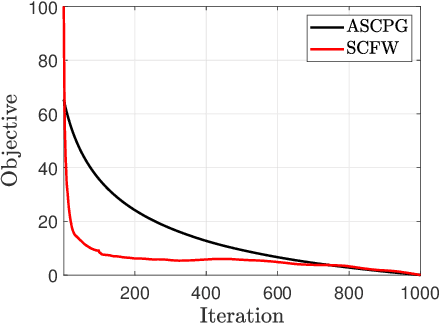
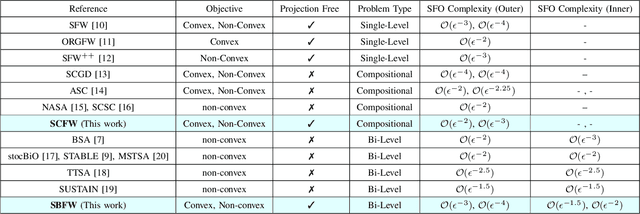
Abstract:This work presents the first projection-free algorithm to solve stochastic bi-level optimization problems, where the objective function depends on the solution of another stochastic optimization problem. The proposed $\textbf{S}$tochastic $\textbf{Bi}$-level $\textbf{F}$rank-$\textbf{W}$olfe ($\textbf{SBFW}$) algorithm can be applied to streaming settings and does not make use of large batches or checkpoints. The sample complexity of SBFW is shown to be $\mathcal{O}(\epsilon^{-3})$ for convex objectives and $\mathcal{O}(\epsilon^{-4})$ for non-convex objectives. Improved rates are derived for the stochastic compositional problem, which is a special case of the bi-level problem, and entails minimizing the composition of two expected-value functions. The proposed $\textbf{S}$tochastic $\textbf{C}$ompositional $\textbf{F}$rank-$\textbf{W}$olfe ($\textbf{SCFW}$) is shown to achieve a sample complexity of $\mathcal{O}(\epsilon^{-2})$ for convex objectives and $\mathcal{O}(\epsilon^{-3})$ for non-convex objectives, at par with the state-of-the-art sample complexities for projection-free algorithms solving single-level problems. We demonstrate the advantage of the proposed methods by solving the problem of matrix completion with denoising and the problem of policy value evaluation in reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge