FedNew: A Communication-Efficient and Privacy-Preserving Newton-Type Method for Federated Learning

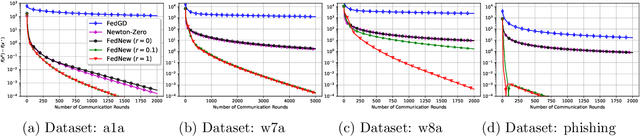
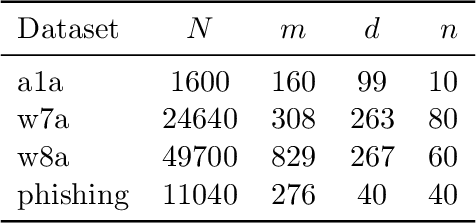
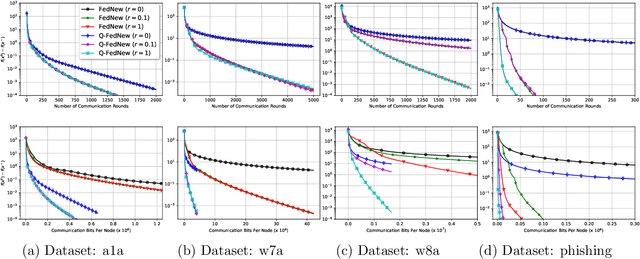
Newton-type methods are popular in federated learning due to their fast convergence. Still, they suffer from two main issues, namely: low communication efficiency and low privacy due to the requirement of sending Hessian information from clients to parameter server (PS). In this work, we introduced a novel framework called FedNew in which there is no need to transmit Hessian information from clients to PS, hence resolving the bottleneck to improve communication efficiency. In addition, FedNew hides the gradient information and results in a privacy-preserving approach compared to the existing state-of-the-art. The core novel idea in FedNew is to introduce a two level framework, and alternate between updating the inverse Hessian-gradient product using only one alternating direction method of multipliers (ADMM) step and then performing the global model update using Newton's method. Though only one ADMM pass is used to approximate the inverse Hessian-gradient product at each iteration, we develop a novel theoretical approach to show the converging behavior of FedNew for convex problems. Additionally, a significant reduction in communication overhead is achieved by utilizing stochastic quantization. Numerical results using real datasets show the superiority of FedNew compared to existing methods in terms of communication costs.

Energy-Efficient and Federated Meta-Learning via Projected Stochastic Gradient Ascent

In this paper, we propose an energy-efficient federated meta-learning framework. The objective is to enable learning a meta-model that can be fine-tuned to a new task with a few number of samples in a distributed setting and at low computation and communication energy consumption. We assume that each task is owned by a separate agent, so a limited number of tasks is used to train a meta-model. Assuming each task was trained offline on the agent's local data, we propose a lightweight algorithm that starts from the local models of all agents, and in a backward manner using projected stochastic gradient ascent (P-SGA) finds a meta-model. The proposed method avoids complex computations such as computing hessian, double looping, and matrix inversion, while achieving high performance at significantly less energy consumption compared to the state-of-the-art methods such as MAML and iMAML on conducted experiments for sinusoid regression and image classification tasks.

Q-GADMM: Quantized Group ADMM for Communication Efficient Decentralized Machine Learning

In this paper, we propose a communication-efficient decentralized machine learning (ML) algorithm, coined quantized group ADMM (Q-GADMM). Every worker in Q-GADMM communicates only with two neighbors, and updates its model via the alternating direct method of multiplier (ADMM), thereby ensuring fast convergence while reducing the number of communication rounds. Furthermore, each worker quantizes its model updates before transmissions, thereby decreasing the communication payload sizes. We prove that Q-GADMM converges for convex loss functions, and numerically show that Q-GADMM yields 7x less communication cost while achieving almost the same accuracy and convergence speed compared to a baseline without quantization, group ADMM (GADMM).

GADMM: Fast and Communication Efficient Framework for Distributed Machine Learning

When the data is distributed across multiple servers, efficient data exchange between the servers (or workers) for solving the distributed learning problem is an important problem and is the focus of this paper. We propose a fast, privacy-aware, and communication-efficient decentralized framework to solve the distributed machine learning (DML) problem. The proposed algorithm, GADMM, is based on Alternating Direct Method of Multiplier (ADMM) algorithm. The key novelty in GADMM is that each worker exchanges the locally trained model only with two neighboring workers, thereby training a global model with lower amount of communication in each exchange. We prove that GADMM converges faster than the centralized batch gradient descent for convex loss functions, and numerically show that it is faster and more communication-efficient than the state-of-the-art communication-efficient centralized algorithms such as the Lazily Aggregated Gradient (LAG), in linear and logistic regression tasks on synthetic and real datasets. Furthermore, we propose Dynamic GADMM (D-GADMM), a variant of GADMM, and prove its convergence under time-varying network topology of the workers.