Decentralized Stochastic Constrained Optimization via Prox-Linearization

This paper studies consensus-based decentralized stochastic optimization for minimizing possibly non-convex expected objectives with convex non-smooth regularizers and nonlinear functional inequality constraints. We reformulate the constrained problem using the exact-penalty model and develop two algorithms that require only local stochastic gradients and first-order constraint information. The first method, Decentralized Stochastic Momentum-based Prox-Linear Algorithm (D-SMPL), combines constraint linearization with a prox-linear step, resulting in a linearly constrained quadratic subproblem per iteration. Building on this approach, we propose a successive convex approximation (SCA) variant, Decentralized SCA Momentum-based Prox-Linear (D-SCAMPL), which handles additional objective structure through strongly convex surrogate subproblems while still allowing infeasible initialization. Both methods incorporate recursive momentum-based gradient estimators and a consensus mechanism requiring only two communication rounds per iteration. Under standard smoothness and regularity assumptions, both algorithms achieve an oracle complexity of $\mathcal{O}(ε^{-3/2})$, matching the optimal rate known for unconstrained centralized stochastic non-convex optimization. Numerical experiments on energy-optimal ocean trajectory planning corroborate the theory and demonstrate improved performance over existing decentralized baselines.

Analysis of Decentralized Stochastic Successive Convex Approximation for composite non-convex problems

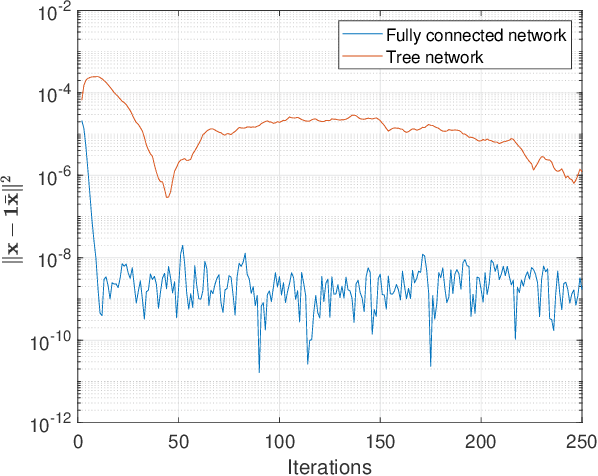
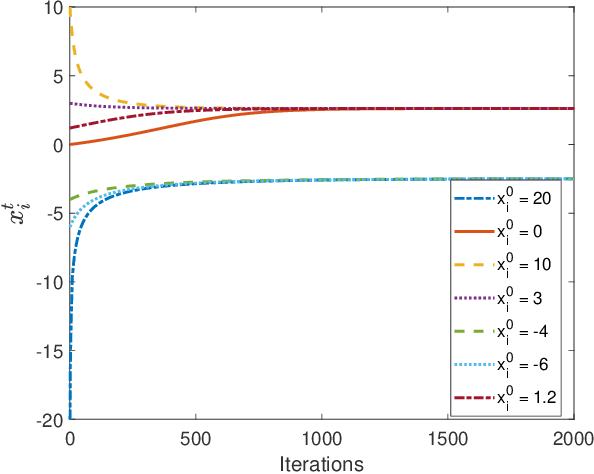
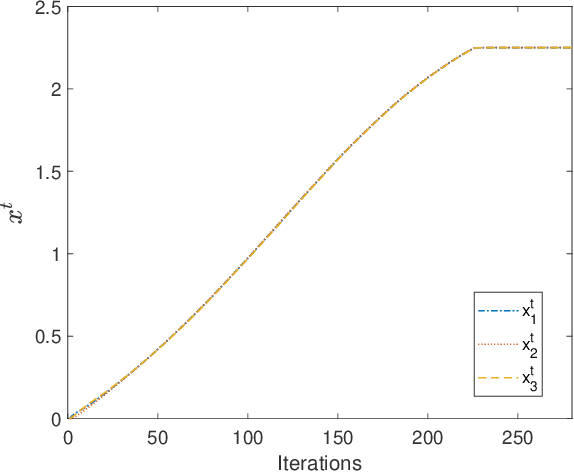
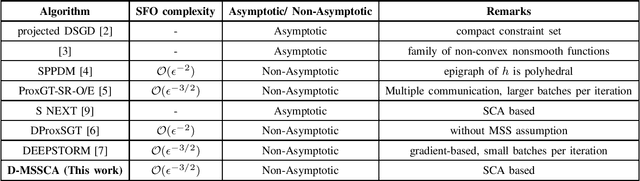
Successive Convex approximation (SCA) methods have shown to improve the empirical convergence of non-convex optimization problems over proximal gradient-based methods. In decentralized optimization, which aims to optimize a global function using only local information, the SCA framework has been successfully applied to achieve improved convergence. Still, the stochastic first order (SFO) complexity of decentralized SCA algorithms has remained understudied. While non-asymptotic convergence analysis has been studied for decentralized deterministic settings, its stochastic counterpart has only been shown to converge asymptotically. We have analyzed a novel accelerated variant of the decentralized stochastic SCA that minimizes the sum of non-convex (possibly smooth) and convex (possibly non-smooth) cost functions. The algorithm viz. Decentralized Momentum-based Stochastic SCA (D-MSSCA), iteratively solves a series of strongly convex subproblems at each node using one sample at each iteration. The key step in non-asymptotic analysis involves proving that the average output state vector moves in the descent direction of the global function. This descent allows us to obtain a bound on average \textit{iterate progress} and \emph{mean-squared stationary gap}. The recursive momentum-based updates at each node contribute to achieving stochastic first order (SFO) complexity of O(\epsilon^{-3/2}) provided that the step sizes are smaller than the given upper bounds. Even with one sample used at each iteration and a non-adaptive step size, the rate is at par with the SFO complexity of decentralized state-of-the-art gradient-based algorithms. The rate also matches the lower bound for the centralized, unconstrained optimization problems. Through a synthetic example, the applicability of D-MSSCA is demonstrated.

Constrained Stochastic Recursive Momentum Successive Convex Approximation

We consider stochastic optimization problems with functional constraints. If the objective and constraint functions are not convex, the classical stochastic approximation algorithms such as the proximal stochastic gradient descent do not lead to efficient algorithms. In this work, we put forth an accelerated SCA algorithm that utilizes the recursive momentum-based acceleration which is widely used in the unconstrained setting. Remarkably, the proposed algorithm also achieves the optimal SFO complexity, at par with that achieved by state-of-the-art (unconstrained) stochastic optimization algorithms and match the SFO-complexity lower bound for minimization of general smooth functions. At each iteration, the proposed algorithm entails constructing convex surrogates of the objective and the constraint functions, and solving the resulting convex optimization problem. A recursive update rule is employed to track the gradient of the objective function, and contributes to achieving faster convergence and improved SFO complexity. A key ingredient of the proof is a new parameterized version of the standard Mangasarian-Fromowitz Constraints Qualification, that allows us to bound the dual variables and hence establish that the iterates approach an $\epsilon$-stationary point. We also detail a obstacle-avoiding trajectory optimization problem that can be solved using the proposed algorithm, and show that its performance is superior to that of the existing algorithms. The performance of the proposed algorithm is also compared against that of a specialized sparse classification algorithm on a binary classification problem.

Practical Precoding via Asynchronous Stochastic Successive Convex Approximation

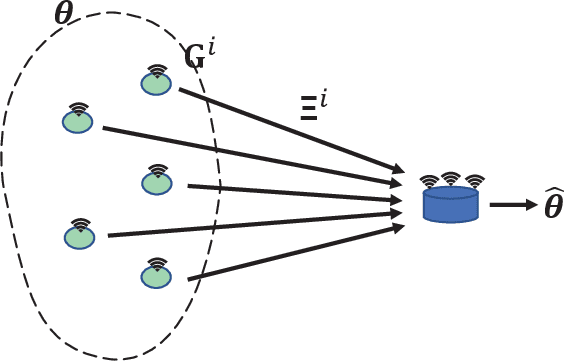
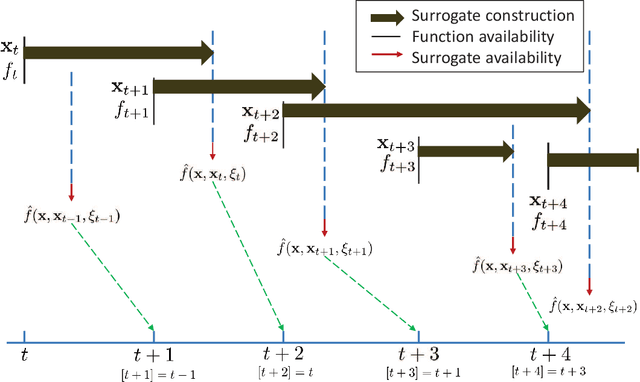
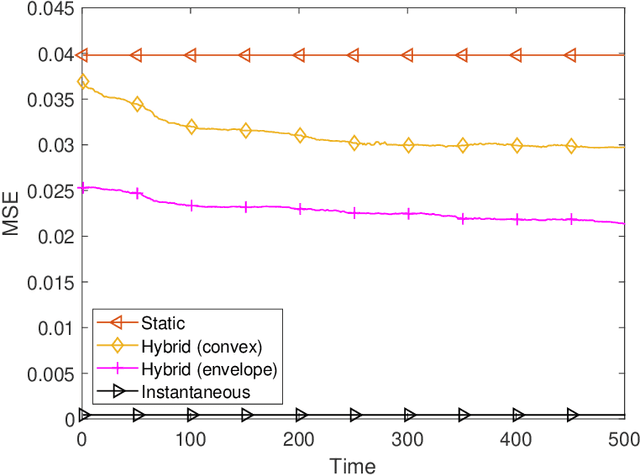
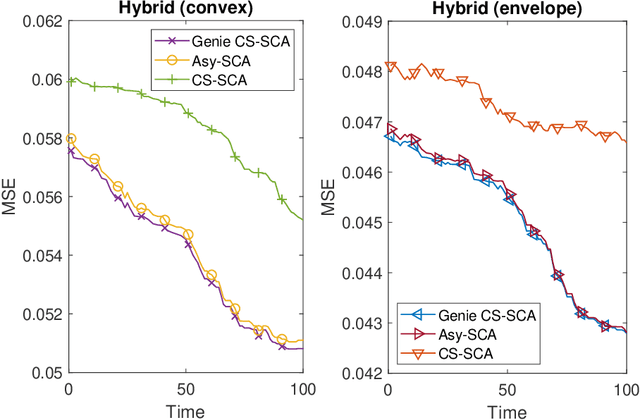
We consider stochastic optimization of a smooth non-convex loss function with a convex non-smooth regularizer. In the online setting, where a single sample of the stochastic gradient of the loss is available at every iteration, the problem can be solved using the proximal stochastic gradient descent (SGD) algorithm and its variants. However in many problems, especially those arising in communications and signal processing, information beyond the stochastic gradient may be available thanks to the structure of the loss function. Such extra-gradient information is not used by SGD, but has been shown to be useful, for instance in the context of stochastic expectation-maximization, stochastic majorization-minimization, and stochastic successive convex approximation (SCA) approaches. By constructing a stochastic strongly convex surrogates of the loss function at every iteration, the stochastic SCA algorithms can exploit the structural properties of the loss function and achieve superior empirical performance as compared to the SGD. In this work, we take a closer look at the stochastic SCA algorithm and develop its asynchronous variant which can be used for resource allocation in wireless networks. While the stochastic SCA algorithm is known to converge asymptotically, its iteration complexity has not been well-studied, and is the focus of the current work. The insights obtained from the non-asymptotic analysis allow us to develop a more practical asynchronous variant of the stochastic SCA algorithm which allows the use of surrogates calculated in earlier iterations. We characterize precise bound on the maximum delay the algorithm can tolerate, while still achieving the same convergence rate. We apply the algorithm to the problem of linear precoding in wireless sensor networks, where it can be implemented at low complexity but is shown to perform well in practice.