Analysis of Decentralized Stochastic Successive Convex Approximation for composite non-convex problems

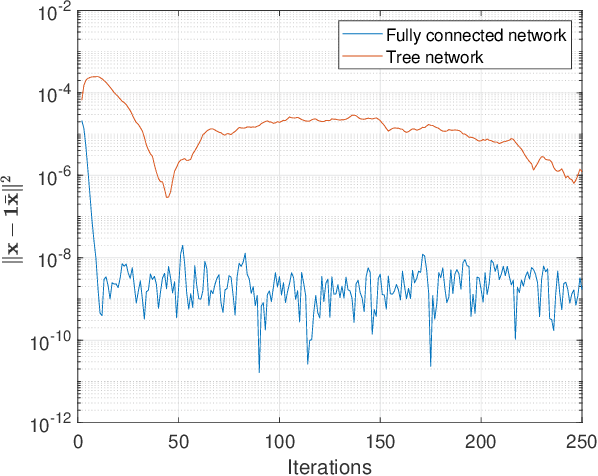
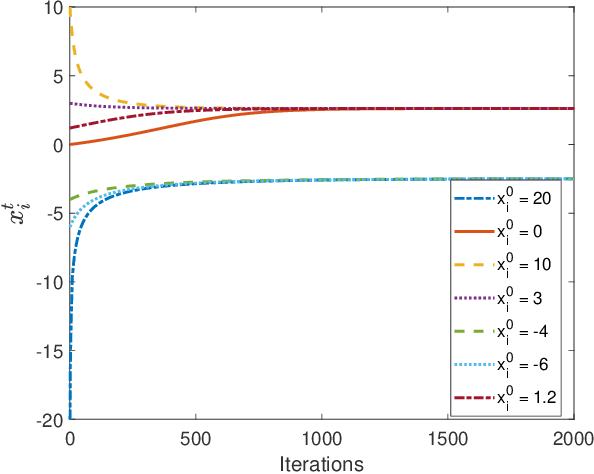
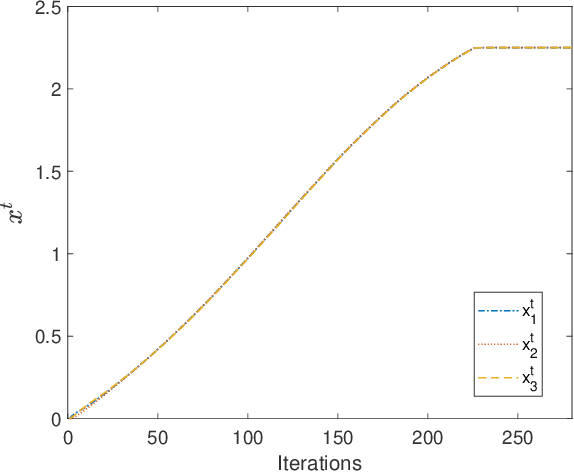
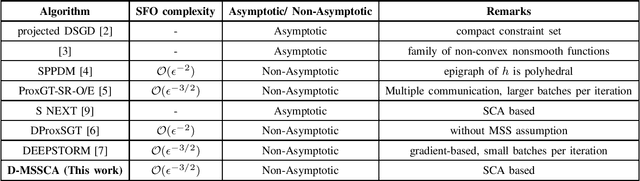
Successive Convex approximation (SCA) methods have shown to improve the empirical convergence of non-convex optimization problems over proximal gradient-based methods. In decentralized optimization, which aims to optimize a global function using only local information, the SCA framework has been successfully applied to achieve improved convergence. Still, the stochastic first order (SFO) complexity of decentralized SCA algorithms has remained understudied. While non-asymptotic convergence analysis has been studied for decentralized deterministic settings, its stochastic counterpart has only been shown to converge asymptotically. We have analyzed a novel accelerated variant of the decentralized stochastic SCA that minimizes the sum of non-convex (possibly smooth) and convex (possibly non-smooth) cost functions. The algorithm viz. Decentralized Momentum-based Stochastic SCA (D-MSSCA), iteratively solves a series of strongly convex subproblems at each node using one sample at each iteration. The key step in non-asymptotic analysis involves proving that the average output state vector moves in the descent direction of the global function. This descent allows us to obtain a bound on average \textit{iterate progress} and \emph{mean-squared stationary gap}. The recursive momentum-based updates at each node contribute to achieving stochastic first order (SFO) complexity of O(\epsilon^{-3/2}) provided that the step sizes are smaller than the given upper bounds. Even with one sample used at each iteration and a non-adaptive step size, the rate is at par with the SFO complexity of decentralized state-of-the-art gradient-based algorithms. The rate also matches the lower bound for the centralized, unconstrained optimization problems. Through a synthetic example, the applicability of D-MSSCA is demonstrated.

Optimized Gradient Tracking for Decentralized Online Learning

This work considers the problem of decentralized online learning, where the goal is to track the optimum of the sum of time-varying functions, distributed across several nodes in a network. The local availability of the functions and their gradients necessitates coordination and consensus among the nodes. We put forth the Generalized Gradient Tracking (GGT) framework that unifies a number of existing approaches, including the state-of-the-art ones. The performance of the proposed GGT algorithm is theoretically analyzed using a novel semidefinite programming-based analysis that yields the desired regret bounds under very general conditions and without requiring the gradient boundedness assumption. The results are applicable to the special cases of GGT, which include various state-of-the-art algorithms as well as new dynamic versions of various classical decentralized algorithms. To further minimize the regret, we consider a condensed version of GGT with only four free parameters. A procedure for offline tuning of these parameters using only the problem parameters is also detailed. The resulting optimized GGT (oGGT) algorithm not only achieves improved dynamic regret bounds, but also outperforms all state-of-the-art algorithms on both synthetic and real-world datasets.