Decentralized Stochastic Constrained Optimization via Prox-Linearization

This paper studies consensus-based decentralized stochastic optimization for minimizing possibly non-convex expected objectives with convex non-smooth regularizers and nonlinear functional inequality constraints. We reformulate the constrained problem using the exact-penalty model and develop two algorithms that require only local stochastic gradients and first-order constraint information. The first method, Decentralized Stochastic Momentum-based Prox-Linear Algorithm (D-SMPL), combines constraint linearization with a prox-linear step, resulting in a linearly constrained quadratic subproblem per iteration. Building on this approach, we propose a successive convex approximation (SCA) variant, Decentralized SCA Momentum-based Prox-Linear (D-SCAMPL), which handles additional objective structure through strongly convex surrogate subproblems while still allowing infeasible initialization. Both methods incorporate recursive momentum-based gradient estimators and a consensus mechanism requiring only two communication rounds per iteration. Under standard smoothness and regularity assumptions, both algorithms achieve an oracle complexity of $\mathcal{O}(ε^{-3/2})$, matching the optimal rate known for unconstrained centralized stochastic non-convex optimization. Numerical experiments on energy-optimal ocean trajectory planning corroborate the theory and demonstrate improved performance over existing decentralized baselines.

Constrained Stochastic Recursive Momentum Successive Convex Approximation

We consider stochastic optimization problems with functional constraints. If the objective and constraint functions are not convex, the classical stochastic approximation algorithms such as the proximal stochastic gradient descent do not lead to efficient algorithms. In this work, we put forth an accelerated SCA algorithm that utilizes the recursive momentum-based acceleration which is widely used in the unconstrained setting. Remarkably, the proposed algorithm also achieves the optimal SFO complexity, at par with that achieved by state-of-the-art (unconstrained) stochastic optimization algorithms and match the SFO-complexity lower bound for minimization of general smooth functions. At each iteration, the proposed algorithm entails constructing convex surrogates of the objective and the constraint functions, and solving the resulting convex optimization problem. A recursive update rule is employed to track the gradient of the objective function, and contributes to achieving faster convergence and improved SFO complexity. A key ingredient of the proof is a new parameterized version of the standard Mangasarian-Fromowitz Constraints Qualification, that allows us to bound the dual variables and hence establish that the iterates approach an $\epsilon$-stationary point. We also detail a obstacle-avoiding trajectory optimization problem that can be solved using the proposed algorithm, and show that its performance is superior to that of the existing algorithms. The performance of the proposed algorithm is also compared against that of a specialized sparse classification algorithm on a binary classification problem.

A Generalized Framework for Autonomous Calibration of Wheeled Mobile Robots

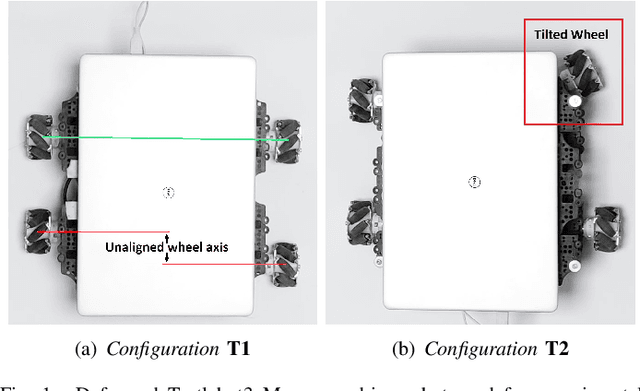
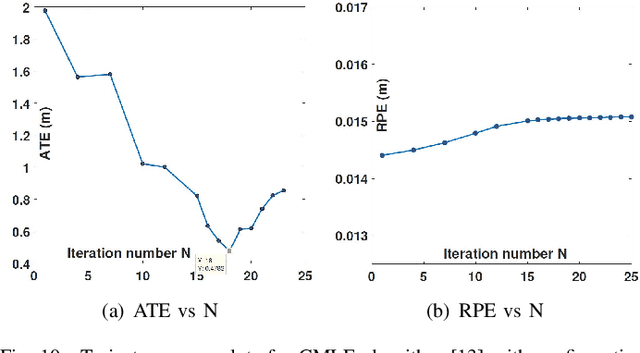
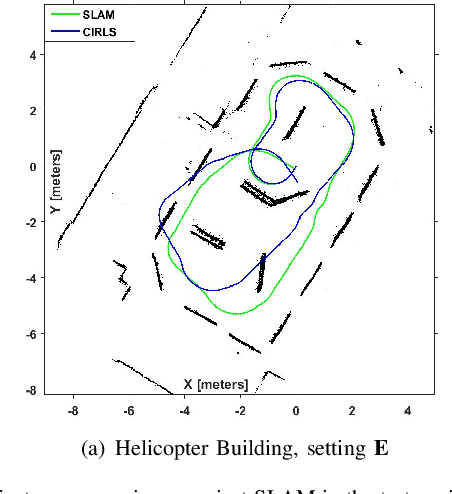
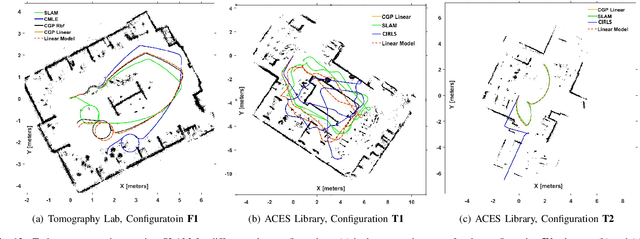
Robotic calibration allows for the fusion of data from multiple sensors such as odometers, cameras, etc., by providing appropriate transformational relationships between the corresponding reference frames. For wheeled robots equipped with exteroceptive sensors, calibration entails learning the motion model of the sensor or the robot in terms of the odometric data, and must generally be performed prior to performing tasks such as simultaneous localization and mapping (SLAM). Within this context, the current trend is to carry out simultaneous calibration of odometry and sensor without the use of any additional hardware. Building upon the existing simultaneous calibration algorithms, we put forth a generalized calibration framework that can not only handle robots operating in 2D with arbitrary or unknown motion models but also handle outliers in an automated manner. We first propose an algorithm based on the alternating minimization framework applicable to two-wheel differential drive. Subsequently, for arbitrary but known drive configurations we put forth an iteratively re-weighted least squares methodology leveraging an intelligent weighing scheme. Different from the existing works, these proposed algorithms require no manual intervention and seamlessly handle outliers that arise due to both systematic and non-systematic errors. Finally, we put forward a novel Gaussian Process-based non-parametric approach for calibrating wheeled robots with arbitrary or unknown drive configurations. Detailed experiments are performed to demonstrate the accuracy, usefulness, and flexibility of the proposed algorithms.

Model Free Calibration of Wheeled Robots Using Gaussian Process

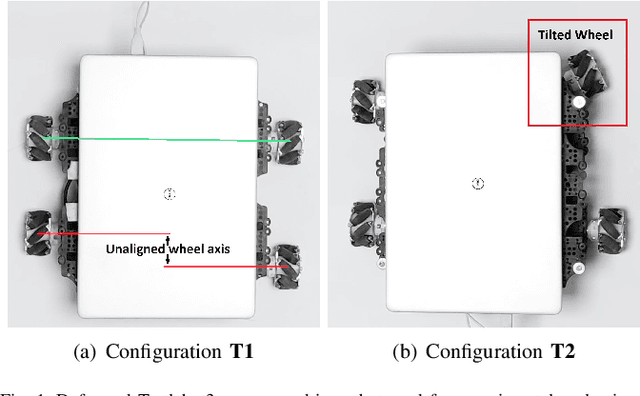
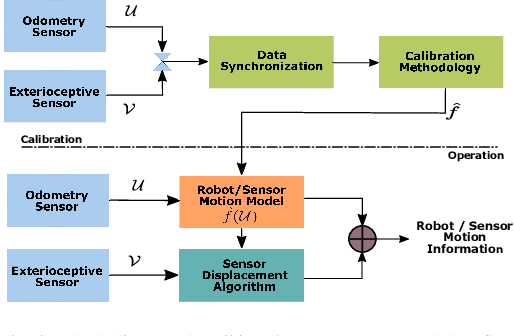
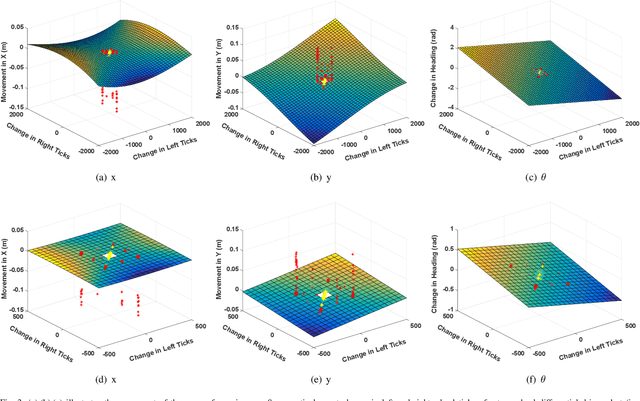
Robotic calibration allows for the fusion of data from multiple sensors such as odometers, cameras, etc., by providing appropriate relationships between the corresponding reference frames. For wheeled robots equipped with camera/lidar along with wheel encoders, calibration entails learning the motion model of the sensor or the robot in terms of the data from the encoders and generally carried out before performing tasks such as simultaneous localization and mapping (SLAM). This work puts forward a novel Gaussian Process-based non-parametric approach for calibrating wheeled robots with arbitrary or unknown drive configurations. The procedure is more general as it learns the entire sensor/robot motion model in terms of odometry measurements. Different from existing non-parametric approaches, our method relies on measurements from the onboard sensors and hence does not require the ground truth information from external motion capture systems. Alternatively, we propose a computationally efficient approach that relies on the linear approximation of the sensor motion model. Finally, we perform experiments to calibrate robots with un-modelled effects to demonstrate the accuracy, usefulness, and flexibility of the proposed approach.