Practical Precoding via Asynchronous Stochastic Successive Convex Approximation
Paper and Code
Oct 03, 2020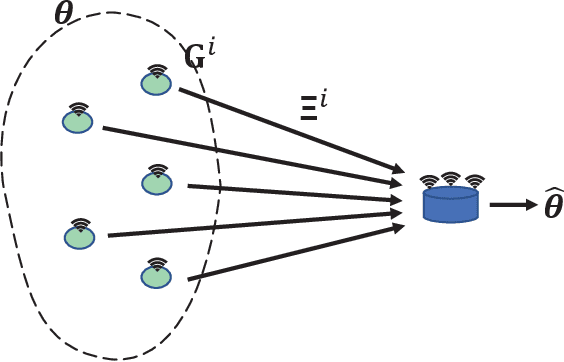
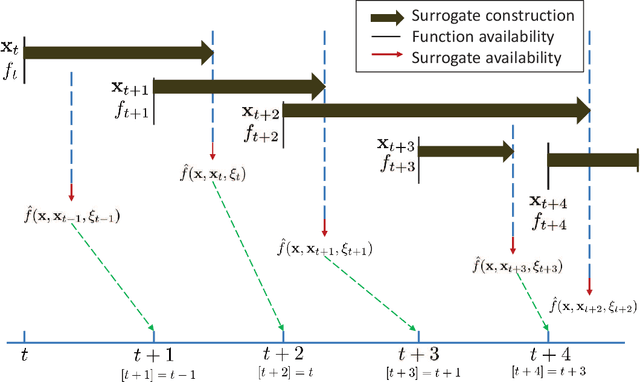
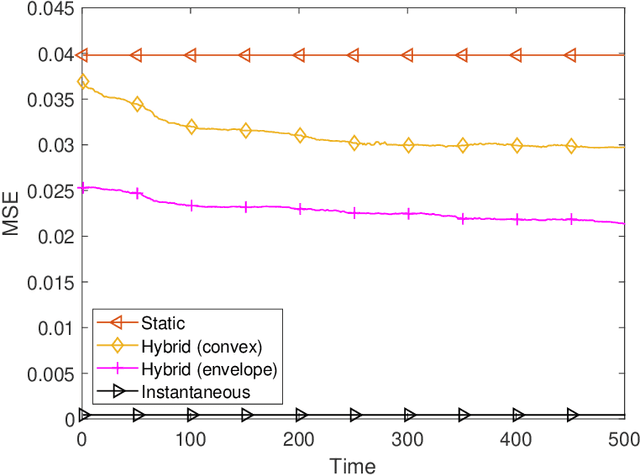
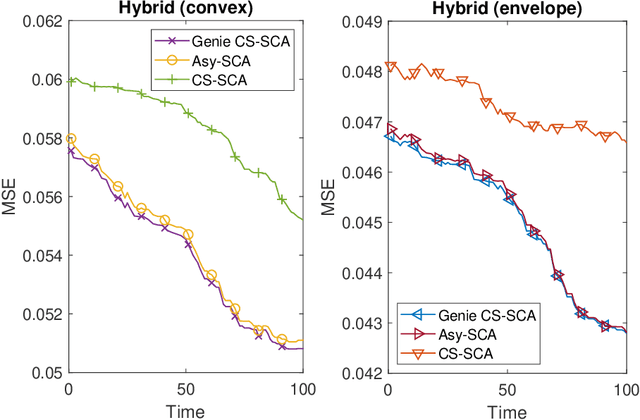
We consider stochastic optimization of a smooth non-convex loss function with a convex non-smooth regularizer. In the online setting, where a single sample of the stochastic gradient of the loss is available at every iteration, the problem can be solved using the proximal stochastic gradient descent (SGD) algorithm and its variants. However in many problems, especially those arising in communications and signal processing, information beyond the stochastic gradient may be available thanks to the structure of the loss function. Such extra-gradient information is not used by SGD, but has been shown to be useful, for instance in the context of stochastic expectation-maximization, stochastic majorization-minimization, and stochastic successive convex approximation (SCA) approaches. By constructing a stochastic strongly convex surrogates of the loss function at every iteration, the stochastic SCA algorithms can exploit the structural properties of the loss function and achieve superior empirical performance as compared to the SGD. In this work, we take a closer look at the stochastic SCA algorithm and develop its asynchronous variant which can be used for resource allocation in wireless networks. While the stochastic SCA algorithm is known to converge asymptotically, its iteration complexity has not been well-studied, and is the focus of the current work. The insights obtained from the non-asymptotic analysis allow us to develop a more practical asynchronous variant of the stochastic SCA algorithm which allows the use of surrogates calculated in earlier iterations. We characterize precise bound on the maximum delay the algorithm can tolerate, while still achieving the same convergence rate. We apply the algorithm to the problem of linear precoding in wireless sensor networks, where it can be implemented at low complexity but is shown to perform well in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge