FAST-PCA: A Fast and Exact Algorithm for Distributed Principal Component Analysis

Principal Component Analysis (PCA) is a fundamental data preprocessing tool in the world of machine learning. While PCA is often reduced to dimension reduction, the purpose of PCA is actually two-fold: dimension reduction and feature learning. Furthermore, the enormity of the dimensions and sample size in the modern day datasets have rendered the centralized PCA solutions unusable. In that vein, this paper reconsiders the problem of PCA when data samples are distributed across nodes in an arbitrarily connected network. While a few solutions for distributed PCA exist those either overlook the feature learning part of the purpose, have communication overhead making them inefficient and/or lack exact convergence guarantees. To combat these aforementioned issues, this paper proposes a distributed PCA algorithm called FAST-PCA (Fast and exAct diSTributed PCA). The proposed algorithm is efficient in terms of communication and can be proved to converge linearly and exactly to the principal components that lead to dimension reduction as well as uncorrelated features. Our claims are further supported by experimental results.

Distributed Principal Subspace Analysis for Partitioned Big Data: Algorithms, Analysis, and Implementation

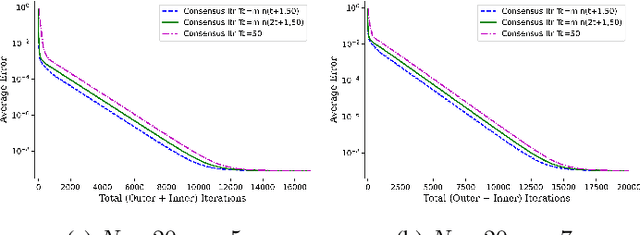
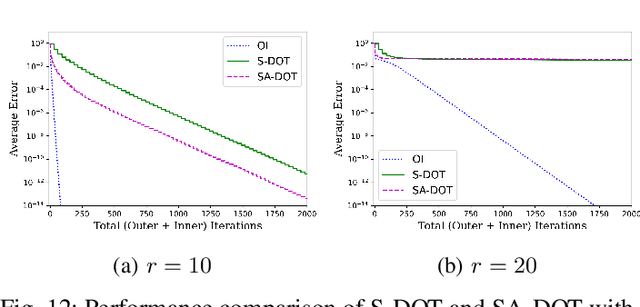
Principal Subspace Analysis (PSA) is one of the most popular approaches for dimensionality reduction in signal processing and machine learning. But centralized PSA solutions are fast becoming irrelevant in the modern era of big data, in which the number of samples and/or the dimensionality of samples often exceed the storage and/or computational capabilities of individual machines. This has led to study of distributed PSA solutions, in which the data are partitioned across multiple machines and an estimate of the principal subspace is obtained through collaboration among the machines. It is in this vein that this paper revisits the problem of distributed PSA under the general framework of an arbitrarily connected network of machines that lacks a central server. The main contributions of the paper in this regard are threefold. First, two algorithms are proposed in the paper that can be used for distributed PSA in the case of data that are partitioned across either samples or (raw) features. Second, in the case of sample-wise partitioned data, the proposed algorithm and a variant of it are analyzed, and their convergence to the true subspace at linear rates is established. Third, extensive experiments on both synthetic and real-world data are carried out to validate the usefulness of the proposed algorithms. In particular, in the case of sample-wise partitioned data, an MPI-based distributed implementation is carried out to study the interplay between network topology and communications cost as well as to study of effect of straggler machines on the proposed algorithms.

A Linearly Convergent Algorithm for Distributed Principal Component Analysis

Principal Component Analysis (PCA) is the workhorse tool for dimensionality reduction in this era of big data. While often overlooked, the purpose of PCA is not only to reduce data dimensionality, but also to yield features that are uncorrelated. This paper focuses on this dual objective of PCA, namely, dimensionality reduction and decorrelation of features, which requires estimating the eigenvectors of a data covariance matrix, as opposed to only estimating the subspace spanned by the eigenvectors. The ever-increasing volume of data in the modern world often requires storage of data samples across multiple machines, which precludes the use of centralized PCA algorithms. Although a few distributed solutions to the PCA problem have been proposed recently, convergence guarantees and/or communications overhead of these solutions remain a concern. With an eye towards communications efficiency, this paper introduces a feedforward neural network-based one time-scale distributed PCA algorithm termed Distributed Sanger's Algorithm (DSA) that estimates the eigenvectors of a data covariance matrix when data are distributed across an undirected and arbitrarily connected network of machines. Furthermore, the proposed algorithm is shown to converge linearly to a neighborhood of the true solution. Numerical results are also shown to demonstrate the efficacy of the proposed solution.

Adversary-resilient Inference and Machine Learning: From Distributed to Decentralized

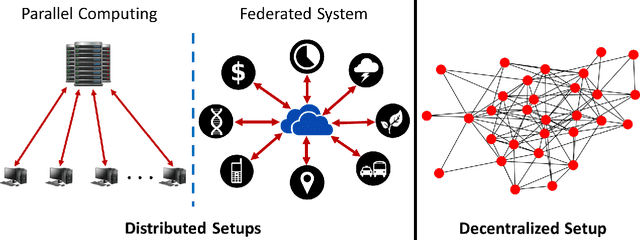
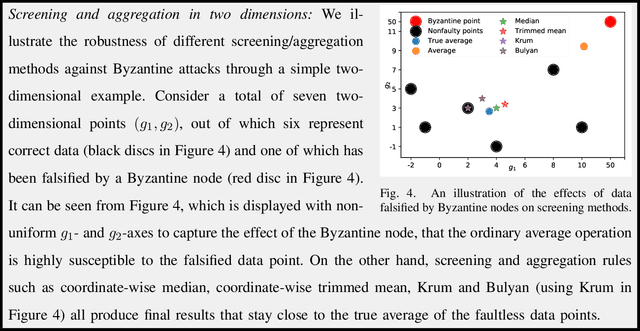
While the last few decades have witnessed a huge body of work devoted to inference and learning in distributed and decentralized setups, much of this work assumes a non-adversarial setting in which individual nodes---apart from occasional statistical failures---operate as intended within the algorithmic framework. In recent years, however, cybersecurity threats from malicious non-state actors and rogue nations have forced practitioners and researchers to rethink the robustness of distributed and decentralized algorithms against adversarial attacks. As a result, we now have a plethora of algorithmic approaches that guarantee robustness of distributed and/or decentralized inference and learning under different adversarial threat models. Driven in part by the world's growing appetite for data-driven decision making, however, securing of distributed/decentralized frameworks for inference and learning against adversarial threats remains a rapidly evolving research area. In this article, we provide an overview of some of the most recent developments in this area under the threat model of Byzantine attacks.