Mohsen Ghassemi
Do LLMs Really Forget? Evaluating Unlearning with Knowledge Correlation and Confidence Awareness
Jun 06, 2025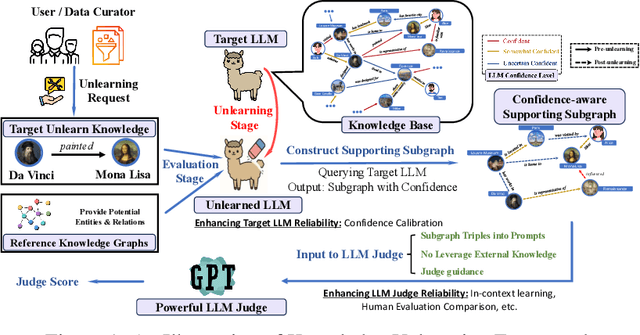
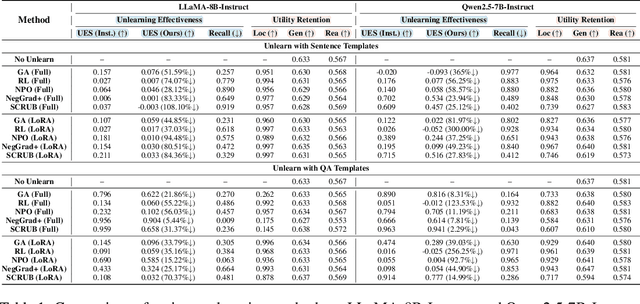
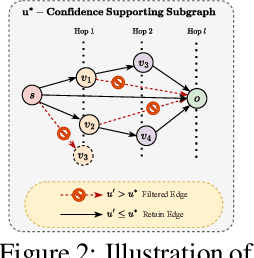
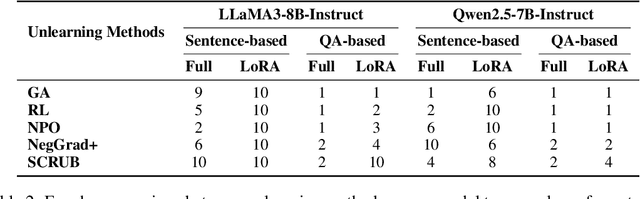
Abstract:Machine unlearning techniques aim to mitigate unintended memorization in large language models (LLMs). However, existing approaches predominantly focus on the explicit removal of isolated facts, often overlooking latent inferential dependencies and the non-deterministic nature of knowledge within LLMs. Consequently, facts presumed forgotten may persist implicitly through correlated information. To address these challenges, we propose a knowledge unlearning evaluation framework that more accurately captures the implicit structure of real-world knowledge by representing relevant factual contexts as knowledge graphs with associated confidence scores. We further develop an inference-based evaluation protocol leveraging powerful LLMs as judges; these judges reason over the extracted knowledge subgraph to determine unlearning success. Our LLM judges utilize carefully designed prompts and are calibrated against human evaluations to ensure their trustworthiness and stability. Extensive experiments on our newly constructed benchmark demonstrate that our framework provides a more realistic and rigorous assessment of unlearning performance. Moreover, our findings reveal that current evaluation strategies tend to overestimate unlearning effectiveness. Our code is publicly available at https://github.com/Graph-COM/Knowledge_Unlearning.git.
Underestimated Privacy Risks for Minority Populations in Large Language Model Unlearning
Dec 11, 2024Abstract:Large Language Models are trained on extensive datasets that often contain sensitive, human-generated information, raising significant concerns about privacy breaches. While certified unlearning approaches offer strong privacy guarantees, they rely on restrictive model assumptions that are not applicable to LLMs. As a result, various unlearning heuristics have been proposed, with the associated privacy risks assessed only empirically. The standard evaluation pipelines typically randomly select data for removal from the training set, apply unlearning techniques, and use membership inference attacks to compare the unlearned models against models retrained without the to-be-unlearned data. However, since every data point is subject to the right to be forgotten, unlearning should be considered in the worst-case scenario from the privacy perspective. Prior work shows that data outliers may exhibit higher memorization effects. Intuitively, they are harder to be unlearn and thus the privacy risk of unlearning them is underestimated in the current evaluation. In this paper, we leverage minority data to identify such a critical flaw in previously widely adopted evaluations. We substantiate this claim through carefully designed experiments, including unlearning canaries related to minority groups, inspired by privacy auditing literature. Using personally identifiable information as a representative minority identifier, we demonstrate that minority groups experience at least 20% more privacy leakage in most cases across six unlearning approaches, three MIAs, three benchmark datasets, and two LLMs of different scales. Given that the right to be forgotten should be upheld for every individual, we advocate for a more rigorous evaluation of LLM unlearning methods. Our minority-aware evaluation framework represents an initial step toward ensuring more equitable assessments of LLM unlearning efficacy.
Auditing and Enforcing Conditional Fairness via Optimal Transport
Oct 17, 2024

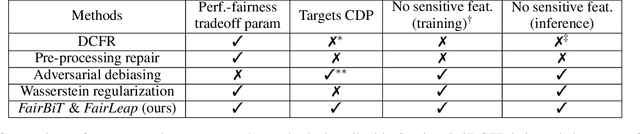

Abstract:Conditional demographic parity (CDP) is a measure of the demographic parity of a predictive model or decision process when conditioning on an additional feature or set of features. Many algorithmic fairness techniques exist to target demographic parity, but CDP is much harder to achieve, particularly when the conditioning variable has many levels and/or when the model outputs are continuous. The problem of auditing and enforcing CDP is understudied in the literature. In light of this, we propose novel measures of {conditional demographic disparity (CDD)} which rely on statistical distances borrowed from the optimal transport literature. We further design and evaluate regularization-based approaches based on these CDD measures. Our methods, \fairbit{} and \fairlp{}, allow us to target CDP even when the conditioning variable has many levels. When model outputs are continuous, our methods target full equality of the conditional distributions, unlike other methods that only consider first moments or related proxy quantities. We validate the efficacy of our approaches on real-world datasets.
Distributionally and Adversarially Robust Logistic Regression via Intersecting Wasserstein Balls
Jul 18, 2024



Abstract:Empirical risk minimization often fails to provide robustness against adversarial attacks in test data, causing poor out-of-sample performance. Adversarially robust optimization (ARO) has thus emerged as the de facto standard for obtaining models that hedge against such attacks. However, while these models are robust against adversarial attacks, they tend to suffer severely from overfitting. To address this issue for logistic regression, we study the Wasserstein distributionally robust (DR) counterpart of ARO and show that this problem admits a tractable reformulation. Furthermore, we develop a framework to reduce the conservatism of this problem by utilizing an auxiliary dataset (e.g., synthetic, external, or out-of-domain data), whenever available, with instances independently sampled from a nonidentical but related ground truth. In particular, we intersect the ambiguity set of the DR problem with another Wasserstein ambiguity set that is built using the auxiliary dataset. We analyze the properties of the underlying optimization problem, develop efficient solution algorithms, and demonstrate that the proposed method consistently outperforms benchmark approaches on real-world datasets.
Synthetic Data Applications in Finance
Dec 29, 2023

Abstract:Synthetic data has made tremendous strides in various commercial settings including finance, healthcare, and virtual reality. We present a broad overview of prototypical applications of synthetic data in the financial sector and in particular provide richer details for a few select ones. These cover a wide variety of data modalities including tabular, time-series, event-series, and unstructured arising from both markets and retail financial applications. Since finance is a highly regulated industry, synthetic data is a potential approach for dealing with issues related to privacy, fairness, and explainability. Various metrics are utilized in evaluating the quality and effectiveness of our approaches in these applications. We conclude with open directions in synthetic data in the context of the financial domain.
Fast Learning of Multidimensional Hawkes Processes via Frank-Wolfe
Dec 12, 2022



Abstract:Hawkes processes have recently risen to the forefront of tools when it comes to modeling and generating sequential events data. Multidimensional Hawkes processes model both the self and cross-excitation between different types of events and have been applied successfully in various domain such as finance, epidemiology and personalized recommendations, among others. In this work we present an adaptation of the Frank-Wolfe algorithm for learning multidimensional Hawkes processes. Experimental results show that our approach has better or on par accuracy in terms of parameter estimation than other first order methods, while enjoying a significantly faster runtime.
Online Learning for Mixture of Multivariate Hawkes Processes
Aug 16, 2022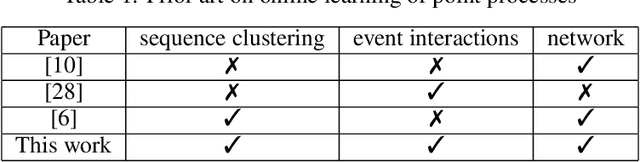

Abstract:Online learning of Hawkes processes has received increasing attention in the last couple of years especially for modeling a network of actors. However, these works typically either model the rich interaction between the events or the latent cluster of the actors or the network structure between the actors. We propose to model the latent structure of the network of actors as well as their rich interaction across events for real-world settings of medical and financial applications. Experimental results on both synthetic and real-world data showcase the efficacy of our approach.
Differentially Private Learning of Hawkes Processes
Jul 27, 2022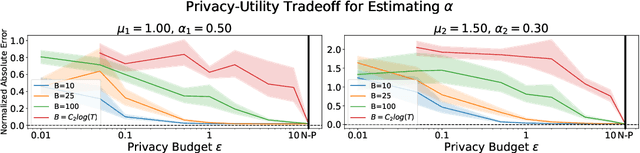
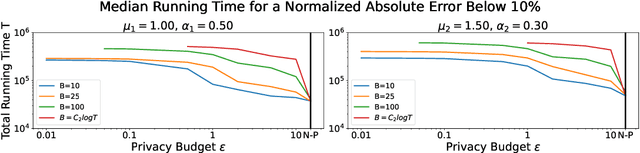
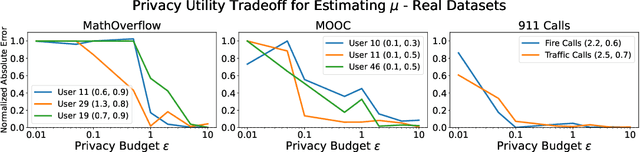
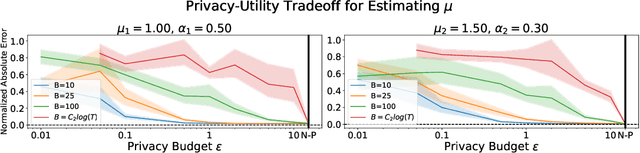
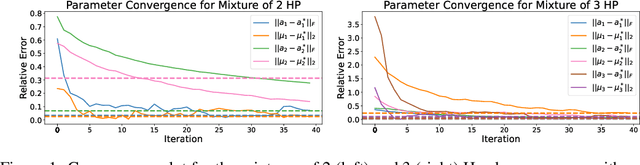
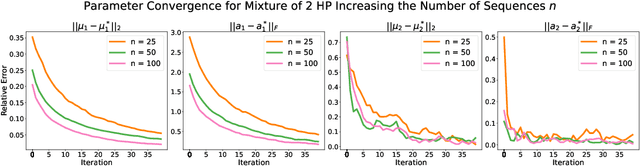
Abstract:Hawkes processes have recently gained increasing attention from the machine learning community for their versatility in modeling event sequence data. While they have a rich history going back decades, some of their properties, such as sample complexity for learning the parameters and releasing differentially private versions, are yet to be thoroughly analyzed. In this work, we study standard Hawkes processes with background intensity $\mu$ and excitation function $\alpha e^{-\beta t}$. We provide both non-private and differentially private estimators of $\mu$ and $\alpha$, and obtain sample complexity results in both settings to quantify the cost of privacy. Our analysis exploits the strong mixing property of Hawkes processes and classical central limit theorem results for weakly dependent random variables. We validate our theoretical findings on both synthetic and real datasets.
A Minimax Lower Bound for Low-Rank Matrix-Variate Logistic Regression
May 31, 2021Abstract:This paper considers the problem of matrix-variate logistic regression. The fundamental error threshold on estimating coefficient matrices in the logistic regression problem is found by deriving a lower bound on the minimax risk. The focus of this paper is on derivation of a minimax risk lower bound for low-rank coefficient matrices. The bound depends explicitly on the dimensions and distribution of the covariates, the rank and energy of the coefficient matrix, and the number of samples. The resulting bound is proportional to the intrinsic degrees of freedom in the problem, which suggests the sample complexity of the low-rank matrix logistic regression problem can be lower than that for vectorized logistic regression. \color{red}\color{black} The proof techniques utilized in this work also set the stage for development of minimax lower bounds for tensor-variate logistic regression problems.
Learning Mixtures of Separable Dictionaries for Tensor Data: Analysis and Algorithms
Mar 22, 2019
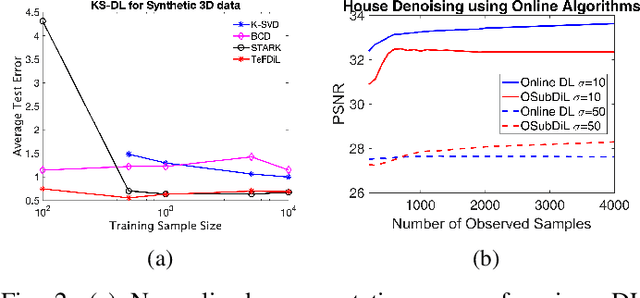
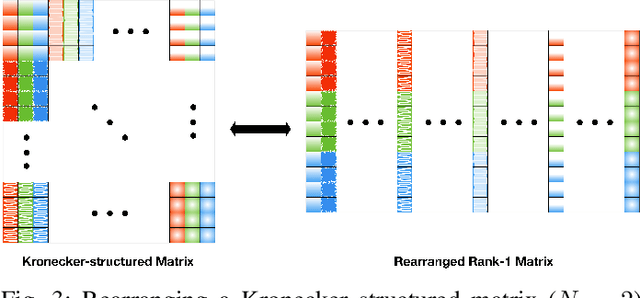
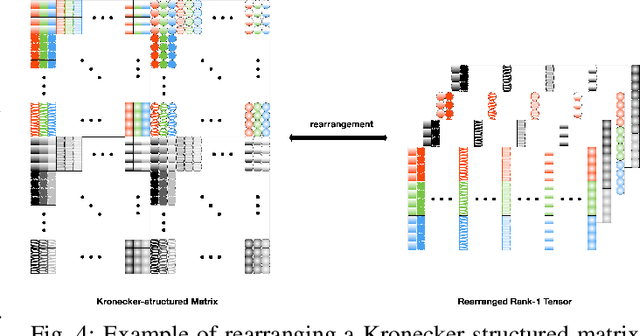
Abstract:This work addresses the problem of learning sparse representations of tensor data using structured dictionary learning. It proposes learning a mixture of separable dictionaries to better capture the structure of tensor data by generalizing the separable dictionary learning model. Two different approaches for learning mixture of separable dictionaries are explored and sufficient conditions for local identifiability of the underlying dictionary are derived in each case. Moreover, computational algorithms are developed to solve the problem of learning mixture of separable dictionaries in both batch and online settings. Numerical experiments are used to show the usefulness of the proposed model and the efficacy of the developed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge