Vamsi K. Potluru
Do LLMs Really Forget? Evaluating Unlearning with Knowledge Correlation and Confidence Awareness
Jun 06, 2025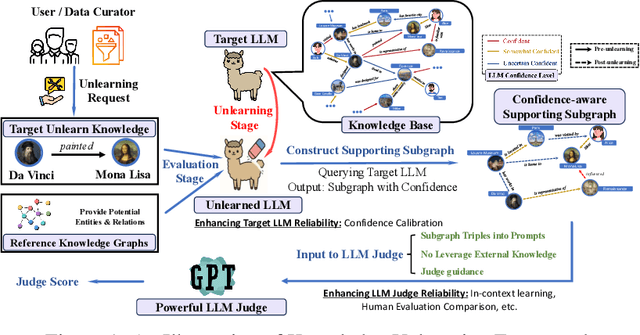
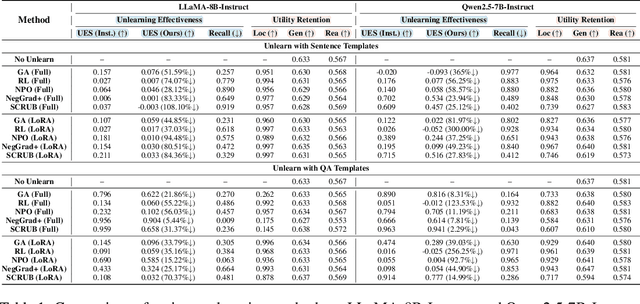
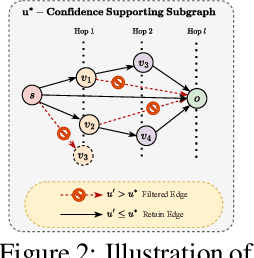
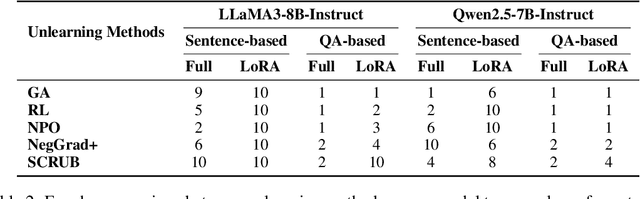
Abstract:Machine unlearning techniques aim to mitigate unintended memorization in large language models (LLMs). However, existing approaches predominantly focus on the explicit removal of isolated facts, often overlooking latent inferential dependencies and the non-deterministic nature of knowledge within LLMs. Consequently, facts presumed forgotten may persist implicitly through correlated information. To address these challenges, we propose a knowledge unlearning evaluation framework that more accurately captures the implicit structure of real-world knowledge by representing relevant factual contexts as knowledge graphs with associated confidence scores. We further develop an inference-based evaluation protocol leveraging powerful LLMs as judges; these judges reason over the extracted knowledge subgraph to determine unlearning success. Our LLM judges utilize carefully designed prompts and are calibrated against human evaluations to ensure their trustworthiness and stability. Extensive experiments on our newly constructed benchmark demonstrate that our framework provides a more realistic and rigorous assessment of unlearning performance. Moreover, our findings reveal that current evaluation strategies tend to overestimate unlearning effectiveness. Our code is publicly available at https://github.com/Graph-COM/Knowledge_Unlearning.git.
Toward Breaking Watermarks in Distortion-free Large Language Models
Feb 25, 2025Abstract:In recent years, LLM watermarking has emerged as an attractive safeguard against AI-generated content, with promising applications in many real-world domains. However, there are growing concerns that the current LLM watermarking schemes are vulnerable to expert adversaries wishing to reverse-engineer the watermarking mechanisms. Prior work in "breaking" or "stealing" LLM watermarks mainly focuses on the distribution-modifying algorithm of Kirchenbauer et al. (2023), which perturbs the logit vector before sampling. In this work, we focus on reverse-engineering the other prominent LLM watermarking scheme, distortion-free watermarking (Kuditipudi et al. 2024), which preserves the underlying token distribution by using a hidden watermarking key sequence. We demonstrate that, even under a more sophisticated watermarking scheme, it is possible to "compromise" the LLM and carry out a "spoofing" attack. Specifically, we propose a mixed integer linear programming framework that accurately estimates the secret key used for watermarking using only a few samples of the watermarked dataset. Our initial findings challenge the current theoretical claims on the robustness and usability of existing LLM watermarking techniques.
Underestimated Privacy Risks for Minority Populations in Large Language Model Unlearning
Dec 11, 2024Abstract:Large Language Models are trained on extensive datasets that often contain sensitive, human-generated information, raising significant concerns about privacy breaches. While certified unlearning approaches offer strong privacy guarantees, they rely on restrictive model assumptions that are not applicable to LLMs. As a result, various unlearning heuristics have been proposed, with the associated privacy risks assessed only empirically. The standard evaluation pipelines typically randomly select data for removal from the training set, apply unlearning techniques, and use membership inference attacks to compare the unlearned models against models retrained without the to-be-unlearned data. However, since every data point is subject to the right to be forgotten, unlearning should be considered in the worst-case scenario from the privacy perspective. Prior work shows that data outliers may exhibit higher memorization effects. Intuitively, they are harder to be unlearn and thus the privacy risk of unlearning them is underestimated in the current evaluation. In this paper, we leverage minority data to identify such a critical flaw in previously widely adopted evaluations. We substantiate this claim through carefully designed experiments, including unlearning canaries related to minority groups, inspired by privacy auditing literature. Using personally identifiable information as a representative minority identifier, we demonstrate that minority groups experience at least 20% more privacy leakage in most cases across six unlearning approaches, three MIAs, three benchmark datasets, and two LLMs of different scales. Given that the right to be forgotten should be upheld for every individual, we advocate for a more rigorous evaluation of LLM unlearning methods. Our minority-aware evaluation framework represents an initial step toward ensuring more equitable assessments of LLM unlearning efficacy.
Auditing and Enforcing Conditional Fairness via Optimal Transport
Oct 17, 2024

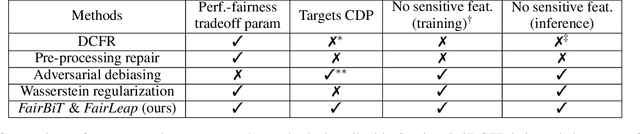

Abstract:Conditional demographic parity (CDP) is a measure of the demographic parity of a predictive model or decision process when conditioning on an additional feature or set of features. Many algorithmic fairness techniques exist to target demographic parity, but CDP is much harder to achieve, particularly when the conditioning variable has many levels and/or when the model outputs are continuous. The problem of auditing and enforcing CDP is understudied in the literature. In light of this, we propose novel measures of {conditional demographic disparity (CDD)} which rely on statistical distances borrowed from the optimal transport literature. We further design and evaluate regularization-based approaches based on these CDD measures. Our methods, \fairbit{} and \fairlp{}, allow us to target CDP even when the conditioning variable has many levels. When model outputs are continuous, our methods target full equality of the conditional distributions, unlike other methods that only consider first moments or related proxy quantities. We validate the efficacy of our approaches on real-world datasets.
Six Levels of Privacy: A Framework for Financial Synthetic Data
Mar 20, 2024Abstract:Synthetic Data is increasingly important in financial applications. In addition to the benefits it provides, such as improved financial modeling and better testing procedures, it poses privacy risks as well. Such data may arise from client information, business information, or other proprietary sources that must be protected. Even though the process by which Synthetic Data is generated serves to obscure the original data to some degree, the extent to which privacy is preserved is hard to assess. Accordingly, we introduce a hierarchy of ``levels'' of privacy that are useful for categorizing Synthetic Data generation methods and the progressively improved protections they offer. While the six levels were devised in the context of financial applications, they may also be appropriate for other industries as well. Our paper includes: A brief overview of Financial Synthetic Data, how it can be used, how its value can be assessed, privacy risks, and privacy attacks. We close with details of the ``Six Levels'' that include defenses against those attacks.
Downstream Task-Oriented Generative Model Selections on Synthetic Data Training for Fraud Detection Models
Jan 01, 2024Abstract:Devising procedures for downstream task-oriented generative model selections is an unresolved problem of practical importance. Existing studies focused on the utility of a single family of generative models. They provided limited insights on how synthetic data practitioners select the best family generative models for synthetic training tasks given a specific combination of machine learning model class and performance metric. In this paper, we approach the downstream task-oriented generative model selections problem in the case of training fraud detection models and investigate the best practice given different combinations of model interpretability and model performance constraints. Our investigation supports that, while both Neural Network(NN)-based and Bayesian Network(BN)-based generative models are both good to complete synthetic training task under loose model interpretability constrain, the BN-based generative models is better than NN-based when synthetic training fraud detection model under strict model interpretability constrain. Our results provides practical guidance for machine learning practitioner who is interested in replacing their training dataset from real to synthetic, and shed lights on more general downstream task-oriented generative model selection problems.
Synthetic Data Applications in Finance
Dec 29, 2023

Abstract:Synthetic data has made tremendous strides in various commercial settings including finance, healthcare, and virtual reality. We present a broad overview of prototypical applications of synthetic data in the financial sector and in particular provide richer details for a few select ones. These cover a wide variety of data modalities including tabular, time-series, event-series, and unstructured arising from both markets and retail financial applications. Since finance is a highly regulated industry, synthetic data is a potential approach for dealing with issues related to privacy, fairness, and explainability. Various metrics are utilized in evaluating the quality and effectiveness of our approaches in these applications. We conclude with open directions in synthetic data in the context of the financial domain.
Fair Wasserstein Coresets
Nov 09, 2023Abstract:Recent technological advancements have given rise to the ability of collecting vast amounts of data, that often exceed the capacity of commonly used machine learning algorithms. Approaches such as coresets and synthetic data distillation have emerged as frameworks to generate a smaller, yet representative, set of samples for downstream training. As machine learning is increasingly applied to decision-making processes, it becomes imperative for modelers to consider and address biases in the data concerning subgroups defined by factors like race, gender, or other sensitive attributes. Current approaches focus on creating fair synthetic representative samples by optimizing local properties relative to the original samples. These methods, however, are not guaranteed to positively affect the performance or fairness of downstream learning processes. In this work, we present Fair Wasserstein Coresets (FWC), a novel coreset approach which generates fair synthetic representative samples along with sample-level weights to be used in downstream learning tasks. FWC aims to minimize the Wasserstein distance between the original datasets and the weighted synthetic samples while enforcing (an empirical version of) demographic parity, a prominent criterion for algorithmic fairness, via a linear constraint. We show that FWC can be thought of as a constrained version of Lloyd's algorithm for k-medians or k-means clustering. Our experiments, conducted on both synthetic and real datasets, demonstrate the scalability of our approach and highlight the competitive performance of FWC compared to existing fair clustering approaches, even when attempting to enhance the fairness of the latter through fair pre-processing techniques.
FairWASP: Fast and Optimal Fair Wasserstein Pre-processing
Oct 31, 2023Abstract:Recent years have seen a surge of machine learning approaches aimed at reducing disparities in model outputs across different subgroups. In many settings, training data may be used in multiple downstream applications by different users, which means it may be most effective to intervene on the training data itself. In this work, we present FairWASP, a novel pre-processing approach designed to reduce disparities in classification datasets without modifying the original data. FairWASP returns sample-level weights such that the reweighted dataset minimizes the Wasserstein distance to the original dataset while satisfying (an empirical version of) demographic parity, a popular fairness criterion. We show theoretically that integer weights are optimal, which means our method can be equivalently understood as duplicating or eliminating samples. FairWASP can therefore be used to construct datasets which can be fed into any classification method, not just methods which accept sample weights. Our work is based on reformulating the pre-processing task as a large-scale mixed-integer program (MIP), for which we propose a highly efficient algorithm based on the cutting plane method. Experiments on synthetic datasets demonstrate that our proposed optimization algorithm significantly outperforms state-of-the-art commercial solvers in solving both the MIP and its linear program relaxation. Further experiments highlight the competitive performance of FairWASP in reducing disparities while preserving accuracy in downstream classification settings.
On the Inherent Privacy Properties of Discrete Denoising Diffusion Models
Oct 24, 2023



Abstract:Privacy concerns have led to a surge in the creation of synthetic datasets, with diffusion models emerging as a promising avenue. Although prior studies have performed empirical evaluations on these models, there has been a gap in providing a mathematical characterization of their privacy-preserving capabilities. To address this, we present the pioneering theoretical exploration of the privacy preservation inherent in discrete diffusion models (DDMs) for discrete dataset generation. Focusing on per-instance differential privacy (pDP), our framework elucidates the potential privacy leakage for each data point in a given training dataset, offering insights into data preprocessing to reduce privacy risks of the synthetic dataset generation via DDMs. Our bounds also show that training with $s$-sized data points leads to a surge in privacy leakage from $(\epsilon, \mathcal{O}(\frac{1}{s^2\epsilon}))$-pDP to $(\epsilon, \mathcal{O}(\frac{1}{s\epsilon}))$-pDP during the transition from the pure noise to the synthetic clean data phase, and a faster decay in diffusion coefficients amplifies the privacy guarantee. Finally, we empirically verify our theoretical findings on both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge