Toward Breaking Watermarks in Distortion-free Large Language Models

In recent years, LLM watermarking has emerged as an attractive safeguard against AI-generated content, with promising applications in many real-world domains. However, there are growing concerns that the current LLM watermarking schemes are vulnerable to expert adversaries wishing to reverse-engineer the watermarking mechanisms. Prior work in "breaking" or "stealing" LLM watermarks mainly focuses on the distribution-modifying algorithm of Kirchenbauer et al. (2023), which perturbs the logit vector before sampling. In this work, we focus on reverse-engineering the other prominent LLM watermarking scheme, distortion-free watermarking (Kuditipudi et al. 2024), which preserves the underlying token distribution by using a hidden watermarking key sequence. We demonstrate that, even under a more sophisticated watermarking scheme, it is possible to "compromise" the LLM and carry out a "spoofing" attack. Specifically, we propose a mixed integer linear programming framework that accurately estimates the secret key used for watermarking using only a few samples of the watermarked dataset. Our initial findings challenge the current theoretical claims on the robustness and usability of existing LLM watermarking techniques.

Monty Hall and Optimized Conformal Prediction to Improve Decision-Making with LLMs

Large language models (LLMs) are empowering decision-making in several applications, including tool or API usage and answering multiple-choice questions (MCQs). However, they often make overconfident, incorrect predictions, which can be risky in high-stakes settings like healthcare and finance. To mitigate these risks, recent works have used conformal prediction (CP), a model-agnostic framework for distribution-free uncertainty quantification. CP transforms a \emph{score function} into prediction sets that contain the true answer with high probability. While CP provides this coverage guarantee for arbitrary scores, the score quality significantly impacts prediction set sizes. Prior works have relied on LLM logits or other heuristic scores, lacking quality guarantees. We address this limitation by introducing CP-OPT, an optimization framework to learn scores that minimize set sizes while maintaining coverage. Furthermore, inspired by the Monty Hall problem, we extend CP's utility beyond uncertainty quantification to improve accuracy. We propose \emph{conformal revision of questions} (CROQ) to revise the problem by narrowing down the available choices to those in the prediction set. The coverage guarantee of CP ensures that the correct choice is in the revised question prompt with high probability, while the smaller number of choices increases the LLM's chances of answering it correctly. Experiments on MMLU, ToolAlpaca, and TruthfulQA datasets with Gemma-2, Llama-3 and Phi-3 models show that CP-OPT significantly reduces set sizes while maintaining coverage, and CROQ improves accuracy over the standard inference, especially when paired with CP-OPT scores. Together, CP-OPT and CROQ offer a robust framework for improving both the safety and accuracy of LLM-driven decision-making.

Synthetic Data Applications in Finance

Synthetic data has made tremendous strides in various commercial settings including finance, healthcare, and virtual reality. We present a broad overview of prototypical applications of synthetic data in the financial sector and in particular provide richer details for a few select ones. These cover a wide variety of data modalities including tabular, time-series, event-series, and unstructured arising from both markets and retail financial applications. Since finance is a highly regulated industry, synthetic data is a potential approach for dealing with issues related to privacy, fairness, and explainability. Various metrics are utilized in evaluating the quality and effectiveness of our approaches in these applications. We conclude with open directions in synthetic data in the context of the financial domain.

Fair Wasserstein Coresets

Recent technological advancements have given rise to the ability of collecting vast amounts of data, that often exceed the capacity of commonly used machine learning algorithms. Approaches such as coresets and synthetic data distillation have emerged as frameworks to generate a smaller, yet representative, set of samples for downstream training. As machine learning is increasingly applied to decision-making processes, it becomes imperative for modelers to consider and address biases in the data concerning subgroups defined by factors like race, gender, or other sensitive attributes. Current approaches focus on creating fair synthetic representative samples by optimizing local properties relative to the original samples. These methods, however, are not guaranteed to positively affect the performance or fairness of downstream learning processes. In this work, we present Fair Wasserstein Coresets (FWC), a novel coreset approach which generates fair synthetic representative samples along with sample-level weights to be used in downstream learning tasks. FWC aims to minimize the Wasserstein distance between the original datasets and the weighted synthetic samples while enforcing (an empirical version of) demographic parity, a prominent criterion for algorithmic fairness, via a linear constraint. We show that FWC can be thought of as a constrained version of Lloyd's algorithm for k-medians or k-means clustering. Our experiments, conducted on both synthetic and real datasets, demonstrate the scalability of our approach and highlight the competitive performance of FWC compared to existing fair clustering approaches, even when attempting to enhance the fairness of the latter through fair pre-processing techniques.

FairWASP: Fast and Optimal Fair Wasserstein Pre-processing

Recent years have seen a surge of machine learning approaches aimed at reducing disparities in model outputs across different subgroups. In many settings, training data may be used in multiple downstream applications by different users, which means it may be most effective to intervene on the training data itself. In this work, we present FairWASP, a novel pre-processing approach designed to reduce disparities in classification datasets without modifying the original data. FairWASP returns sample-level weights such that the reweighted dataset minimizes the Wasserstein distance to the original dataset while satisfying (an empirical version of) demographic parity, a popular fairness criterion. We show theoretically that integer weights are optimal, which means our method can be equivalently understood as duplicating or eliminating samples. FairWASP can therefore be used to construct datasets which can be fed into any classification method, not just methods which accept sample weights. Our work is based on reformulating the pre-processing task as a large-scale mixed-integer program (MIP), for which we propose a highly efficient algorithm based on the cutting plane method. Experiments on synthetic datasets demonstrate that our proposed optimization algorithm significantly outperforms state-of-the-art commercial solvers in solving both the MIP and its linear program relaxation. Further experiments highlight the competitive performance of FairWASP in reducing disparities while preserving accuracy in downstream classification settings.

Deep Gaussian Mixture Ensembles

This work introduces a novel probabilistic deep learning technique called deep Gaussian mixture ensembles (DGMEs), which enables accurate quantification of both epistemic and aleatoric uncertainty. By assuming the data generating process follows that of a Gaussian mixture, DGMEs are capable of approximating complex probability distributions, such as heavy-tailed or multimodal distributions. Our contributions include the derivation of an expectation-maximization (EM) algorithm used for learning the model parameters, which results in an upper-bound on the log-likelihood of training data over that of standard deep ensembles. Additionally, the proposed EM training procedure allows for learning of mixture weights, which is not commonly done in ensembles. Our experimental results demonstrate that DGMEs outperform state-of-the-art uncertainty quantifying deep learning models in handling complex predictive densities.

Fast Learning of Multidimensional Hawkes Processes via Frank-Wolfe

Hawkes processes have recently risen to the forefront of tools when it comes to modeling and generating sequential events data. Multidimensional Hawkes processes model both the self and cross-excitation between different types of events and have been applied successfully in various domain such as finance, epidemiology and personalized recommendations, among others. In this work we present an adaptation of the Frank-Wolfe algorithm for learning multidimensional Hawkes processes. Experimental results show that our approach has better or on par accuracy in terms of parameter estimation than other first order methods, while enjoying a significantly faster runtime.

Online Learning for Mixture of Multivariate Hawkes Processes

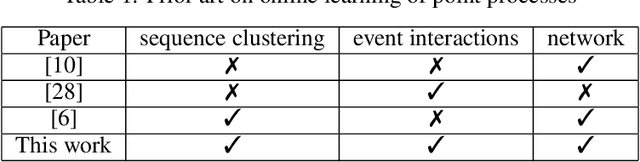
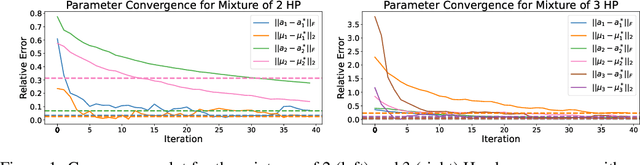
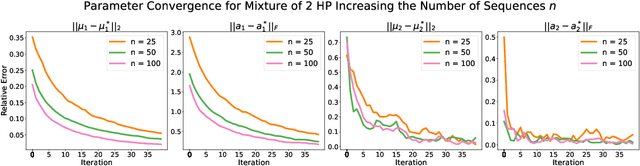
Online learning of Hawkes processes has received increasing attention in the last couple of years especially for modeling a network of actors. However, these works typically either model the rich interaction between the events or the latent cluster of the actors or the network structure between the actors. We propose to model the latent structure of the network of actors as well as their rich interaction across events for real-world settings of medical and financial applications. Experimental results on both synthetic and real-world data showcase the efficacy of our approach.

Differentially Private Learning of Hawkes Processes

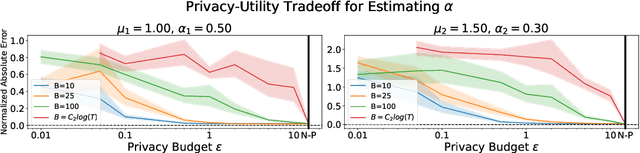
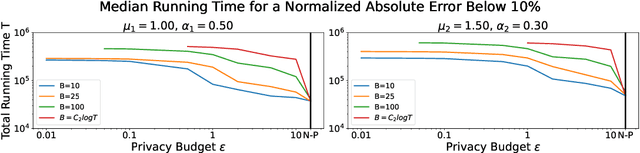
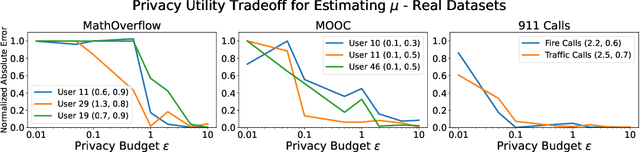
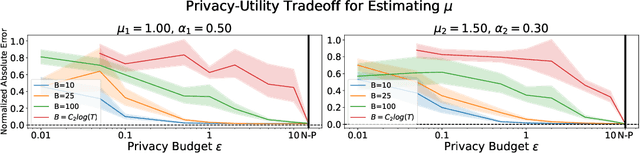
Hawkes processes have recently gained increasing attention from the machine learning community for their versatility in modeling event sequence data. While they have a rich history going back decades, some of their properties, such as sample complexity for learning the parameters and releasing differentially private versions, are yet to be thoroughly analyzed. In this work, we study standard Hawkes processes with background intensity $\mu$ and excitation function $\alpha e^{-\beta t}$. We provide both non-private and differentially private estimators of $\mu$ and $\alpha$, and obtain sample complexity results in both settings to quantify the cost of privacy. Our analysis exploits the strong mixing property of Hawkes processes and classical central limit theorem results for weakly dependent random variables. We validate our theoretical findings on both synthetic and real datasets.

Fair When Trained, Unfair When Deployed: Observable Fairness Measures are Unstable in Performative Prediction Settings

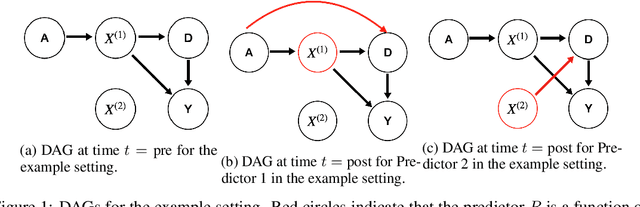
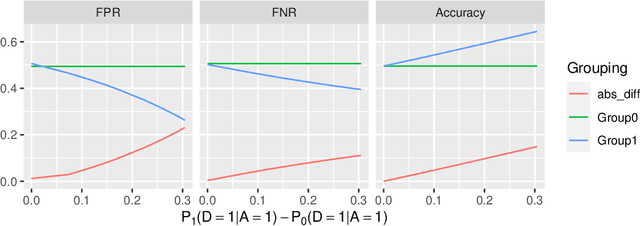
Many popular algorithmic fairness measures depend on the joint distribution of predictions, outcomes, and a sensitive feature like race or gender. These measures are sensitive to distribution shift: a predictor which is trained to satisfy one of these fairness definitions may become unfair if the distribution changes. In performative prediction settings, however, predictors are precisely intended to induce distribution shift. For example, in many applications in criminal justice, healthcare, and consumer finance, the purpose of building a predictor is to reduce the rate of adverse outcomes such as recidivism, hospitalization, or default on a loan. We formalize the effect of such predictors as a type of concept shift-a particular variety of distribution shift-and show both theoretically and via simulated examples how this causes predictors which are fair when they are trained to become unfair when they are deployed. We further show how many of these issues can be avoided by using fairness definitions that depend on counterfactual rather than observable outcomes.