Underestimated Privacy Risks for Minority Populations in Large Language Model Unlearning

Large Language Models are trained on extensive datasets that often contain sensitive, human-generated information, raising significant concerns about privacy breaches. While certified unlearning approaches offer strong privacy guarantees, they rely on restrictive model assumptions that are not applicable to LLMs. As a result, various unlearning heuristics have been proposed, with the associated privacy risks assessed only empirically. The standard evaluation pipelines typically randomly select data for removal from the training set, apply unlearning techniques, and use membership inference attacks to compare the unlearned models against models retrained without the to-be-unlearned data. However, since every data point is subject to the right to be forgotten, unlearning should be considered in the worst-case scenario from the privacy perspective. Prior work shows that data outliers may exhibit higher memorization effects. Intuitively, they are harder to be unlearn and thus the privacy risk of unlearning them is underestimated in the current evaluation. In this paper, we leverage minority data to identify such a critical flaw in previously widely adopted evaluations. We substantiate this claim through carefully designed experiments, including unlearning canaries related to minority groups, inspired by privacy auditing literature. Using personally identifiable information as a representative minority identifier, we demonstrate that minority groups experience at least 20% more privacy leakage in most cases across six unlearning approaches, three MIAs, three benchmark datasets, and two LLMs of different scales. Given that the right to be forgotten should be upheld for every individual, we advocate for a more rigorous evaluation of LLM unlearning methods. Our minority-aware evaluation framework represents an initial step toward ensuring more equitable assessments of LLM unlearning efficacy.

Synthetic Data Applications in Finance

Synthetic data has made tremendous strides in various commercial settings including finance, healthcare, and virtual reality. We present a broad overview of prototypical applications of synthetic data in the financial sector and in particular provide richer details for a few select ones. These cover a wide variety of data modalities including tabular, time-series, event-series, and unstructured arising from both markets and retail financial applications. Since finance is a highly regulated industry, synthetic data is a potential approach for dealing with issues related to privacy, fairness, and explainability. Various metrics are utilized in evaluating the quality and effectiveness of our approaches in these applications. We conclude with open directions in synthetic data in the context of the financial domain.

On the Inherent Privacy Properties of Discrete Denoising Diffusion Models

Privacy concerns have led to a surge in the creation of synthetic datasets, with diffusion models emerging as a promising avenue. Although prior studies have performed empirical evaluations on these models, there has been a gap in providing a mathematical characterization of their privacy-preserving capabilities. To address this, we present the pioneering theoretical exploration of the privacy preservation inherent in discrete diffusion models (DDMs) for discrete dataset generation. Focusing on per-instance differential privacy (pDP), our framework elucidates the potential privacy leakage for each data point in a given training dataset, offering insights into data preprocessing to reduce privacy risks of the synthetic dataset generation via DDMs. Our bounds also show that training with $s$-sized data points leads to a surge in privacy leakage from $(\epsilon, \mathcal{O}(\frac{1}{s^2\epsilon}))$-pDP to $(\epsilon, \mathcal{O}(\frac{1}{s\epsilon}))$-pDP during the transition from the pure noise to the synthetic clean data phase, and a faster decay in diffusion coefficients amplifies the privacy guarantee. Finally, we empirically verify our theoretical findings on both synthetic and real-world datasets.

GraphMaker: Can Diffusion Models Generate Large Attributed Graphs?

Large-scale graphs with node attributes are fundamental in real-world scenarios, such as social and financial networks. The generation of synthetic graphs that emulate real-world ones is pivotal in graph machine learning, aiding network evolution understanding and data utility preservation when original data cannot be shared. Traditional models for graph generation suffer from limited model capacity. Recent developments in diffusion models have shown promise in merely graph structure generation or the generation of small molecular graphs with attributes. However, their applicability to large attributed graphs remains unaddressed due to challenges in capturing intricate patterns and scalability. This paper introduces GraphMaker, a novel diffusion model tailored for generating large attributed graphs. We study the diffusion models that either couple or decouple graph structure and node attribute generation to address their complex correlation. We also employ node-level conditioning and adopt a minibatch strategy for scalability. We further propose a new evaluation pipeline using models trained on generated synthetic graphs and tested on original graphs to evaluate the quality of synthetic data. Empirical evaluations on real-world datasets showcase GraphMaker's superiority in generating realistic and diverse large-attributed graphs beneficial for downstream tasks.

Differentially Private Synthetic Data Using KD-Trees

Creation of a synthetic dataset that faithfully represents the data distribution and simultaneously preserves privacy is a major research challenge. Many space partitioning based approaches have emerged in recent years for answering statistical queries in a differentially private manner. However, for synthetic data generation problem, recent research has been mainly focused on deep generative models. In contrast, we exploit space partitioning techniques together with noise perturbation and thus achieve intuitive and transparent algorithms. We propose both data independent and data dependent algorithms for $\epsilon$-differentially private synthetic data generation whose kernel density resembles that of the real dataset. Additionally, we provide theoretical results on the utility-privacy trade-offs and show how our data dependent approach overcomes the curse of dimensionality and leads to a scalable algorithm. We show empirical utility improvements over the prior work, and discuss performance of our algorithm on a downstream classification task on a real dataset.

Differentially Private Learning of Hawkes Processes

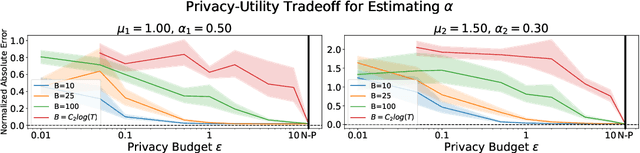
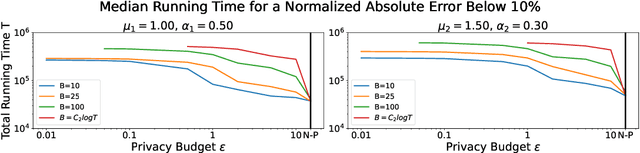
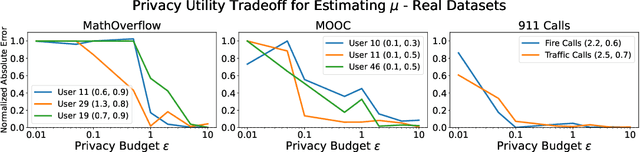
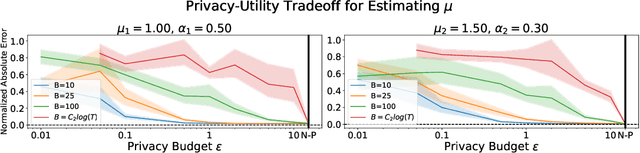
Hawkes processes have recently gained increasing attention from the machine learning community for their versatility in modeling event sequence data. While they have a rich history going back decades, some of their properties, such as sample complexity for learning the parameters and releasing differentially private versions, are yet to be thoroughly analyzed. In this work, we study standard Hawkes processes with background intensity $\mu$ and excitation function $\alpha e^{-\beta t}$. We provide both non-private and differentially private estimators of $\mu$ and $\alpha$, and obtain sample complexity results in both settings to quantify the cost of privacy. Our analysis exploits the strong mixing property of Hawkes processes and classical central limit theorem results for weakly dependent random variables. We validate our theoretical findings on both synthetic and real datasets.