Eli Chien
Differentially Private Relational Learning with Entity-level Privacy Guarantees
Jun 10, 2025Abstract:Learning with relational and network-structured data is increasingly vital in sensitive domains where protecting the privacy of individual entities is paramount. Differential Privacy (DP) offers a principled approach for quantifying privacy risks, with DP-SGD emerging as a standard mechanism for private model training. However, directly applying DP-SGD to relational learning is challenging due to two key factors: (i) entities often participate in multiple relations, resulting in high and difficult-to-control sensitivity; and (ii) relational learning typically involves multi-stage, potentially coupled (interdependent) sampling procedures that make standard privacy amplification analyses inapplicable. This work presents a principled framework for relational learning with formal entity-level DP guarantees. We provide a rigorous sensitivity analysis and introduce an adaptive gradient clipping scheme that modulates clipping thresholds based on entity occurrence frequency. We also extend the privacy amplification results to a tractable subclass of coupled sampling, where the dependence arises only through sample sizes. These contributions lead to a tailored DP-SGD variant for relational data with provable privacy guarantees. Experiments on fine-tuning text encoders over text-attributed network-structured relational data demonstrate the strong utility-privacy trade-offs of our approach. Our code is available at https://github.com/Graph-COM/Node_DP.
Do LLMs Really Forget? Evaluating Unlearning with Knowledge Correlation and Confidence Awareness
Jun 06, 2025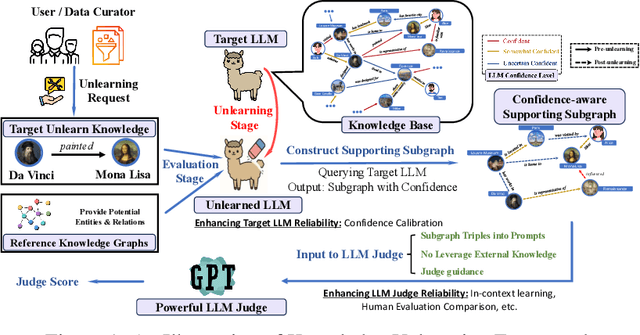
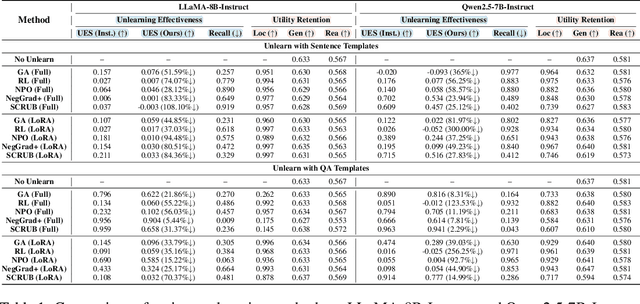
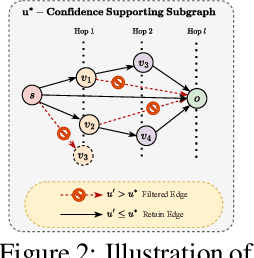
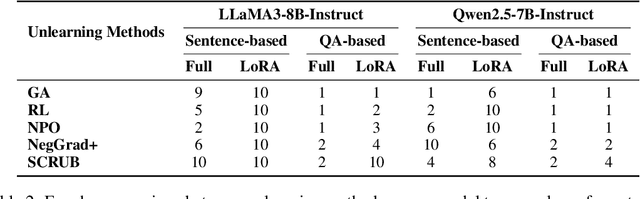
Abstract:Machine unlearning techniques aim to mitigate unintended memorization in large language models (LLMs). However, existing approaches predominantly focus on the explicit removal of isolated facts, often overlooking latent inferential dependencies and the non-deterministic nature of knowledge within LLMs. Consequently, facts presumed forgotten may persist implicitly through correlated information. To address these challenges, we propose a knowledge unlearning evaluation framework that more accurately captures the implicit structure of real-world knowledge by representing relevant factual contexts as knowledge graphs with associated confidence scores. We further develop an inference-based evaluation protocol leveraging powerful LLMs as judges; these judges reason over the extracted knowledge subgraph to determine unlearning success. Our LLM judges utilize carefully designed prompts and are calibrated against human evaluations to ensure their trustworthiness and stability. Extensive experiments on our newly constructed benchmark demonstrate that our framework provides a more realistic and rigorous assessment of unlearning performance. Moreover, our findings reveal that current evaluation strategies tend to overestimate unlearning effectiveness. Our code is publicly available at https://github.com/Graph-COM/Knowledge_Unlearning.git.
Underestimated Privacy Risks for Minority Populations in Large Language Model Unlearning
Dec 11, 2024Abstract:Large Language Models are trained on extensive datasets that often contain sensitive, human-generated information, raising significant concerns about privacy breaches. While certified unlearning approaches offer strong privacy guarantees, they rely on restrictive model assumptions that are not applicable to LLMs. As a result, various unlearning heuristics have been proposed, with the associated privacy risks assessed only empirically. The standard evaluation pipelines typically randomly select data for removal from the training set, apply unlearning techniques, and use membership inference attacks to compare the unlearned models against models retrained without the to-be-unlearned data. However, since every data point is subject to the right to be forgotten, unlearning should be considered in the worst-case scenario from the privacy perspective. Prior work shows that data outliers may exhibit higher memorization effects. Intuitively, they are harder to be unlearn and thus the privacy risk of unlearning them is underestimated in the current evaluation. In this paper, we leverage minority data to identify such a critical flaw in previously widely adopted evaluations. We substantiate this claim through carefully designed experiments, including unlearning canaries related to minority groups, inspired by privacy auditing literature. Using personally identifiable information as a representative minority identifier, we demonstrate that minority groups experience at least 20% more privacy leakage in most cases across six unlearning approaches, three MIAs, three benchmark datasets, and two LLMs of different scales. Given that the right to be forgotten should be upheld for every individual, we advocate for a more rigorous evaluation of LLM unlearning methods. Our minority-aware evaluation framework represents an initial step toward ensuring more equitable assessments of LLM unlearning efficacy.
LayerDAG: A Layerwise Autoregressive Diffusion Model for Directed Acyclic Graph Generation
Nov 04, 2024



Abstract:Directed acyclic graphs (DAGs) serve as crucial data representations in domains such as hardware synthesis and compiler/program optimization for computing systems. DAG generative models facilitate the creation of synthetic DAGs, which can be used for benchmarking computing systems while preserving intellectual property. However, generating realistic DAGs is challenging due to their inherent directional and logical dependencies. This paper introduces LayerDAG, an autoregressive diffusion model, to address these challenges. LayerDAG decouples the strong node dependencies into manageable units that can be processed sequentially. By interpreting the partial order of nodes as a sequence of bipartite graphs, LayerDAG leverages autoregressive generation to model directional dependencies and employs diffusion models to capture logical dependencies within each bipartite graph. Comparative analyses demonstrate that LayerDAG outperforms existing DAG generative models in both expressiveness and generalization, particularly for generating large-scale DAGs with up to 400 nodes-a critical scenario for system benchmarking. Extensive experiments on both synthetic and real-world flow graphs from various computing platforms show that LayerDAG generates valid DAGs with superior statistical properties and benchmarking performance. The synthetic DAGs generated by LayerDAG enhance the training of ML-based surrogate models, resulting in improved accuracy in predicting performance metrics of real-world DAGs across diverse computing platforms.
Privately Learning from Graphs with Applications in Fine-tuning Large Language Models
Oct 10, 2024



Abstract:Graphs offer unique insights into relationships and interactions between entities, complementing data modalities like text, images, and videos. By incorporating relational information from graph data, AI models can extend their capabilities beyond traditional tasks. However, relational data in sensitive domains such as finance and healthcare often contain private information, making privacy preservation crucial. Existing privacy-preserving methods, such as DP-SGD, which rely on gradient decoupling assumptions, are not well-suited for relational learning due to the inherent dependencies between coupled training samples. To address this challenge, we propose a privacy-preserving relational learning pipeline that decouples dependencies in sampled relations during training, ensuring differential privacy through a tailored application of DP-SGD. We apply this method to fine-tune large language models (LLMs) on sensitive graph data, and tackle the associated computational complexities. Our approach is evaluated on LLMs of varying sizes (e.g., BERT, Llama2) using real-world relational data from four text-attributed graphs. The results demonstrate significant improvements in relational learning tasks, all while maintaining robust privacy guarantees during training. Additionally, we explore the trade-offs between privacy, utility, and computational efficiency, offering insights into the practical deployment of our approach. Code is available at https://github.com/Graph-COM/PvGaLM.
Convergent Privacy Loss of Noisy-SGD without Convexity and Smoothness
Oct 01, 2024


Abstract:We study the Differential Privacy (DP) guarantee of hidden-state Noisy-SGD algorithms over a bounded domain. Standard privacy analysis for Noisy-SGD assumes all internal states are revealed, which leads to a divergent R'enyi DP bound with respect to the number of iterations. Ye & Shokri (2022) and Altschuler & Talwar (2022) proved convergent bounds for smooth (strongly) convex losses, and raise open questions about whether these assumptions can be relaxed. We provide positive answers by proving convergent R'enyi DP bound for non-convex non-smooth losses, where we show that requiring losses to have H\"older continuous gradient is sufficient. We also provide a strictly better privacy bound compared to state-of-the-art results for smooth strongly convex losses. Our analysis relies on the improvement of shifted divergence analysis in multiple aspects, including forward Wasserstein distance tracking, identifying the optimal shifts allocation, and the H"older reduction lemma. Our results further elucidate the benefit of hidden-state analysis for DP and its applicability.
Differentially Private Graph Diffusion with Applications in Personalized PageRanks
Jul 02, 2024



Abstract:Graph diffusion, which iteratively propagates real-valued substances among the graph, is used in numerous graph/network-involved applications. However, releasing diffusion vectors may reveal sensitive linking information in the data such as transaction information in financial network data. However, protecting the privacy of graph data is challenging due to its interconnected nature. This work proposes a novel graph diffusion framework with edge-level differential privacy guarantees by using noisy diffusion iterates. The algorithm injects Laplace noise per diffusion iteration and adopts a degree-based thresholding function to mitigate the high sensitivity induced by low-degree nodes. Our privacy loss analysis is based on Privacy Amplification by Iteration (PABI), which to our best knowledge, is the first effort that analyzes PABI with Laplace noise and provides relevant applications. We also introduce a novel Infinity-Wasserstein distance tracking method, which tightens the analysis of privacy leakage and makes PABI more applicable in practice. We evaluate this framework by applying it to Personalized Pagerank computation for ranking tasks. Experiments on real-world network data demonstrate the superiority of our method under stringent privacy conditions.
Stochastic Gradient Langevin Unlearning
Mar 25, 2024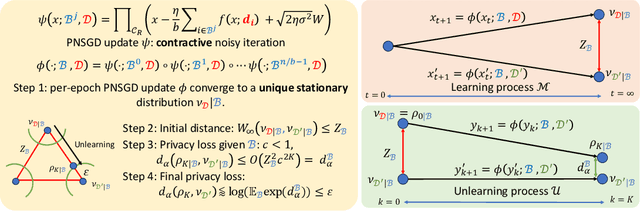
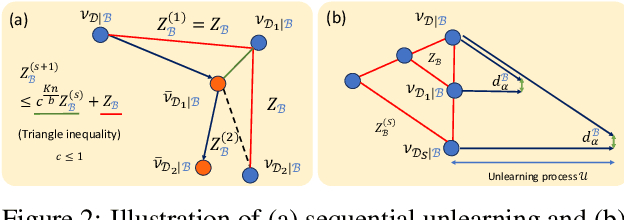

Abstract:``The right to be forgotten'' ensured by laws for user data privacy becomes increasingly important. Machine unlearning aims to efficiently remove the effect of certain data points on the trained model parameters so that it can be approximately the same as if one retrains the model from scratch. This work proposes stochastic gradient Langevin unlearning, the first unlearning framework based on noisy stochastic gradient descent (SGD) with privacy guarantees for approximate unlearning problems under convexity assumption. Our results show that mini-batch gradient updates provide a superior privacy-complexity trade-off compared to the full-batch counterpart. There are numerous algorithmic benefits of our unlearning approach, including complexity saving compared to retraining, and supporting sequential and batch unlearning. To examine the privacy-utility-complexity trade-off of our method, we conduct experiments on benchmark datasets compared against prior works. Our approach achieves a similar utility under the same privacy constraint while using $2\%$ and $10\%$ of the gradient computations compared with the state-of-the-art gradient-based approximate unlearning methods for mini-batch and full-batch settings, respectively.
Machine Unlearning of Pre-trained Large Language Models
Feb 27, 2024Abstract:This study investigates the concept of the `right to be forgotten' within the context of large language models (LLMs). We explore machine unlearning as a pivotal solution, with a focus on pre-trained models--a notably under-researched area. Our research delineates a comprehensive framework for machine unlearning in pre-trained LLMs, encompassing a critical analysis of seven diverse unlearning methods. Through rigorous evaluation using curated datasets from arXiv, books, and GitHub, we establish a robust benchmark for unlearning performance, demonstrating that these methods are over $10^5$ times more computationally efficient than retraining. Our results show that integrating gradient ascent with gradient descent on in-distribution data improves hyperparameter robustness. We also provide detailed guidelines for efficient hyperparameter tuning in the unlearning process. Our findings advance the discourse on ethical AI practices, offering substantive insights into the mechanics of machine unlearning for pre-trained LLMs and underscoring the potential for responsible AI development.
Langevin Unlearning: A New Perspective of Noisy Gradient Descent for Machine Unlearning
Feb 01, 2024



Abstract:Machine unlearning has raised significant interest with the adoption of laws ensuring the ``right to be forgotten''. Researchers have provided a probabilistic notion of approximate unlearning under a similar definition of Differential Privacy (DP), where privacy is defined as statistical indistinguishability to retraining from scratch. We propose Langevin unlearning, an unlearning framework based on noisy gradient descent with privacy guarantees for approximate unlearning problems. Langevin unlearning unifies the DP learning process and the privacy-certified unlearning process with many algorithmic benefits. These include approximate certified unlearning for non-convex problems, complexity saving compared to retraining, sequential and batch unlearning for multiple unlearning requests. We verify the practicality of Langevin unlearning by studying its privacy-utility-complexity trade-off via experiments on benchmark datasets, and also demonstrate its superiority against gradient-decent-plus-output-perturbation based approximate unlearning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge