A Benchmark on Directed Graph Representation Learning in Hardware Designs

To keep pace with the rapid advancements in design complexity within modern computing systems, directed graph representation learning (DGRL) has become crucial, particularly for encoding circuit netlists, computational graphs, and developing surrogate models for hardware performance prediction. However, DGRL remains relatively unexplored, especially in the hardware domain, mainly due to the lack of comprehensive and user-friendly benchmarks. This study presents a novel benchmark comprising five hardware design datasets and 13 prediction tasks spanning various levels of circuit abstraction. We evaluate 21 DGRL models, employing diverse graph neural networks and graph transformers (GTs) as backbones, enhanced by positional encodings (PEs) tailored for directed graphs. Our results highlight that bidirected (BI) message passing neural networks (MPNNs) and robust PEs significantly enhance model performance. Notably, the top-performing models include PE-enhanced GTs interleaved with BI-MPNN layers and BI-Graph Isomorphism Network, both surpassing baselines across the 13 tasks. Additionally, our investigation into out-of-distribution (OOD) performance emphasizes the urgent need to improve OOD generalization in DGRL models. This benchmark, implemented with a modular codebase, streamlines the evaluation of DGRL models for both hardware and ML practitioners

What Are Good Positional Encodings for Directed Graphs?

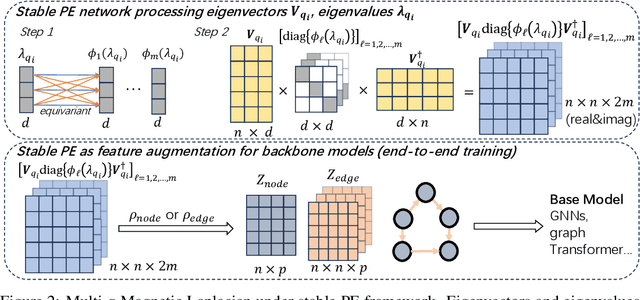
Positional encodings (PE) for graphs are essential in constructing powerful and expressive graph neural networks and graph transformers as they effectively capture relative spatial relations between nodes. While PEs for undirected graphs have been extensively studied, those for directed graphs remain largely unexplored, despite the fundamental role of directed graphs in representing entities with strong logical dependencies, such as those in program analysis and circuit designs. This work studies the design of PEs for directed graphs that are expressive to represent desired directed spatial relations. We first propose walk profile, a generalization of walk counting sequence to directed graphs. We identify limitations in existing PE methods, including symmetrized Laplacian PE, Singular Value Decomposition PE, and Magnetic Laplacian PE, in their ability to express walk profiles. To address these limitations, we propose the Multi-q Magnetic Laplacian PE, which extends Magnetic Laplacian PE with multiple potential factors. This simple variant turns out to be capable of provably expressing walk profiles. Furthermore, we generalize previous basis-invariant and stable networks to handle complex-domain PEs decomposed from Magnetic Laplacians. Our numerical experiments demonstrate the effectiveness of Multi-q Magnetic Laplacian PE with a stable neural architecture, outperforming previous PE methods (with stable networks) on predicting directed distances/walk profiles, sorting network satisfiability, and on general circuit benchmarks. Our code is available at https://github.com/Graph-COM/Multi-q-Maglap.

What Can We Learn from State Space Models for Machine Learning on Graphs?

Machine learning on graphs has recently found extensive applications across domains. However, the commonly used Message Passing Neural Networks (MPNNs) suffer from limited expressive power and struggle to capture long-range dependencies. Graph transformers offer a strong alternative due to their global attention mechanism, but they come with great computational overheads, especially for large graphs. In recent years, State Space Models (SSMs) have emerged as a compelling approach to replace full attention in transformers to model sequential data. It blends the strengths of RNNs and CNNs, offering a) efficient computation, b) the ability to capture long-range dependencies, and c) good generalization across sequences of various lengths. However, extending SSMs to graph-structured data presents unique challenges due to the lack of canonical node ordering in graphs. In this work, we propose Graph State Space Convolution (GSSC) as a principled extension of SSMs to graph-structured data. By leveraging global permutation-equivariant set aggregation and factorizable graph kernels that rely on relative node distances as the convolution kernels, GSSC preserves all three advantages of SSMs. We demonstrate the provably stronger expressiveness of GSSC than MPNNs in counting graph substructures and show its effectiveness across 10 real-world, widely used benchmark datasets, where GSSC achieves best results on 7 out of 10 datasets with all significant improvements compared to the state-of-the-art baselines and second-best results on the other 3 datasets. Our findings highlight the potential of GSSC as a powerful and scalable model for graph machine learning. Our code is available at https://github.com/Graph-COM/GSSC.

On the Stability of Expressive Positional Encodings for Graph Neural Networks

Designing effective positional encodings for graphs is key to building powerful graph transformers and enhancing message-passing graph neural networks. Although widespread, using Laplacian eigenvectors as positional encodings faces two fundamental challenges: (1) \emph{Non-uniqueness}: there are many different eigendecompositions of the same Laplacian, and (2) \emph{Instability}: small perturbations to the Laplacian could result in completely different eigenspaces, leading to unpredictable changes in positional encoding. Despite many attempts to address non-uniqueness, most methods overlook stability, leading to poor generalization on unseen graph structures. We identify the cause of instability to be a "hard partition" of eigenspaces. Hence, we introduce Stable and Expressive Positional Encodings (SPE), an architecture for processing eigenvectors that uses eigenvalues to "softly partition" eigenspaces. SPE is the first architecture that is (1) provably stable, and (2) universally expressive for basis invariant functions whilst respecting all symmetries of eigenvectors. Besides guaranteed stability, we prove that SPE is at least as expressive as existing methods, and highly capable of counting graph structures. Finally, we evaluate the effectiveness of our method on molecular property prediction, and out-of-distribution generalization tasks, finding improved generalization compared to existing positional encoding methods.

Is Distance Matrix Enough for Geometric Deep Learning?

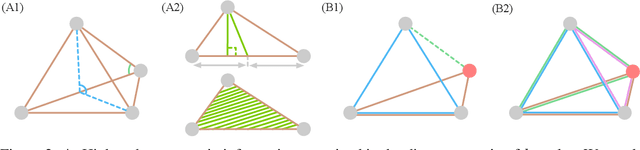
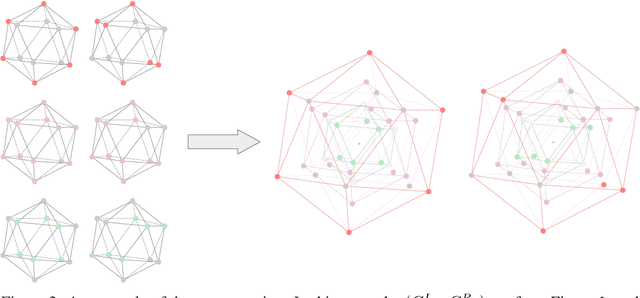
Graph Neural Networks (GNNs) are often used for tasks involving the geometry of a given graph, such as molecular dynamics simulation. While the distance matrix of a graph contains the complete geometric structure information, whether GNNs can learn this geometry solely from the distance matrix has yet to be studied. In this work, we first demonstrate that Message Passing Neural Networks (MPNNs) are insufficient for learning the geometry of a graph from its distance matrix by constructing families of geometric graphs which cannot be distinguished by MPNNs. We then propose $k$-DisGNNs, which can effectively exploit the rich geometry contained in the distance matrix. We demonstrate the high expressive power of our models and prove that some existing well-designed geometric models can be unified by $k$-DisGNNs as special cases. Most importantly, we establish a connection between geometric deep learning and traditional graph representation learning, showing that those highly expressive GNN models originally designed for graph structure learning can also be applied to geometric deep learning problems with impressive performance, and that existing complex, equivariant models are not the only solution. Experimental results verify our theory.

3DLinker: An E(3) Equivariant Variational Autoencoder for Molecular Linker Design

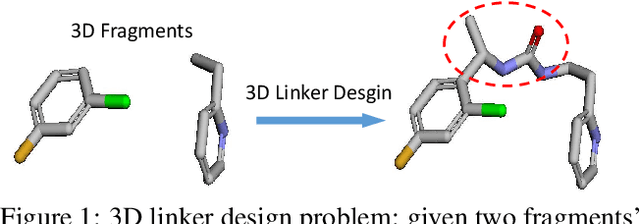
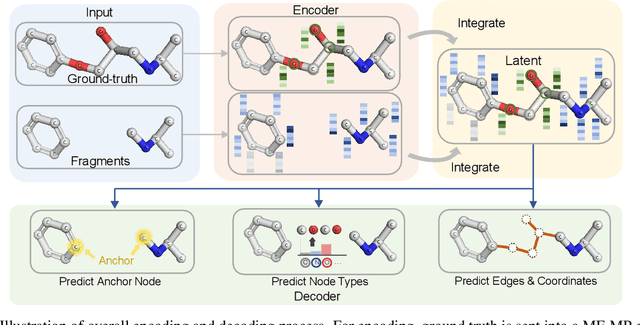
Deep learning has achieved tremendous success in designing novel chemical compounds with desirable pharmaceutical properties. In this work, we focus on a new type of drug design problem -- generating a small "linker" to physically attach two independent molecules with their distinct functions. The main computational challenges include: 1) the generation of linkers is conditional on the two given molecules, in contrast to generating full molecules from scratch in previous works; 2) linkers heavily depend on the anchor atoms of the two molecules to be connected, which are not known beforehand; 3) 3D structures and orientations of the molecules need to be considered to avoid atom clashes, for which equivariance to E(3) group are necessary. To address these problems, we propose a conditional generative model, named 3DLinker, which is able to predict anchor atoms and jointly generate linker graphs and their 3D structures based on an E(3) equivariant graph variational autoencoder. So far as we know, there are no previous models that could achieve this task. We compare our model with multiple conditional generative models modified from other molecular design tasks and find that our model has a significantly higher rate in recovering molecular graphs, and more importantly, accurately predicting the 3D coordinates of all the atoms.