What Affects the Effective Depth of Large Language Models?

The scaling of large language models (LLMs) emphasizes increasing depth, yet performance gains diminish with added layers. Prior work introduces the concept of "effective depth", arguing that deeper models fail to fully utilize their layers for meaningful computation. Building on this, we systematically study how effective depth varies with model scale, training type, and task difficulty. First, we analyze the model behavior of Qwen-2.5 family (1.5B-32B) and find that while the number of effective layers grows with model size, the effective depth ratio remains stable. Besides, comparisons between base and corresponding long-CoT models show no increase in effective depth, suggesting that improved reasoning stems from longer context rather than deeper per-token computation. Furthermore, evaluations across tasks of varying difficulty indicate that models do not dynamically use more layers for harder problems. Our results suggest that current LLMs underuse available depth across scales, training paradigms and tasks of varying difficulties, pointing out research opportunities on increasing the layer utilization rate of LLMs, model pruning, and early exiting. Our code is released at https://github.com/AheadOFpotato/what_affects_effective_depth.

Diffusion As Self-Distillation: End-to-End Latent Diffusion In One Model

Standard Latent Diffusion Models rely on a complex, three-part architecture consisting of a separate encoder, decoder, and diffusion network, which are trained in multiple stages. This modular design is computationally inefficient, leads to suboptimal performance, and prevents the unification of diffusion with the single-network architectures common in vision foundation models. Our goal is to unify these three components into a single, end-to-end trainable network. We first demonstrate that a naive joint training approach fails catastrophically due to ``latent collapse'', where the diffusion training objective interferes with the network's ability to learn a good latent representation. We identify the root causes of this instability by drawing a novel analogy between diffusion and self-distillation based unsupervised learning method. Based on this insight, we propose Diffusion as Self-Distillation (DSD), a new framework with key modifications to the training objective that stabilize the latent space. This approach enables, for the first time, the stable end-to-end training of a single network that simultaneously learns to encode, decode, and perform diffusion. DSD achieves outstanding performance on the ImageNet $256\times 256$ conditional generation task: FID=13.44/6.38/4.25 with only 42M/118M/205M parameters and 50 training epochs on ImageNet, without using classifier-free-guidance.

GRIP: In-Parameter Graph Reasoning through Fine-Tuning Large Language Models

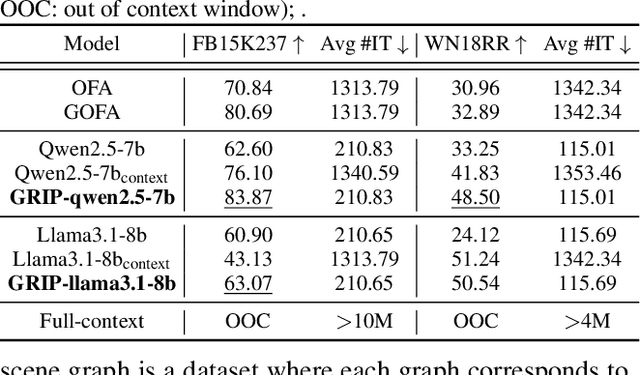
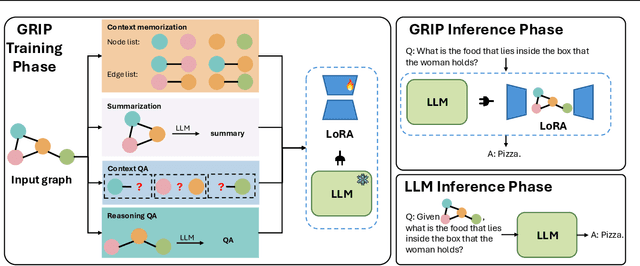
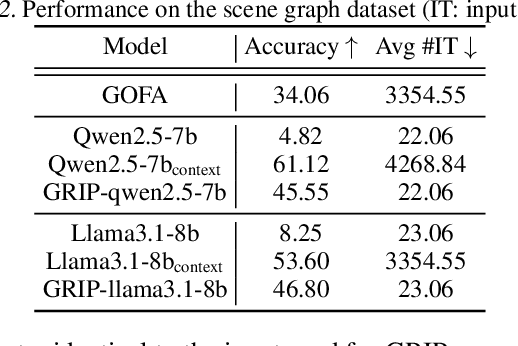
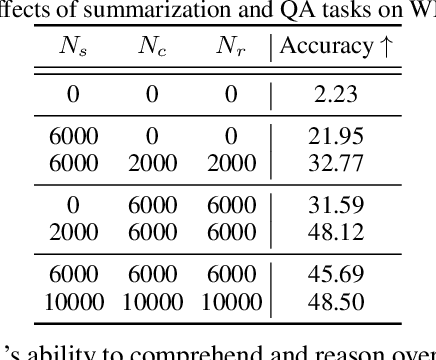
Large Language Models (LLMs) have demonstrated remarkable capabilities in modeling sequential textual data and generalizing across diverse tasks. However, adapting LLMs to effectively handle structural data, such as knowledge graphs or web data, remains a challenging problem. Some approaches adopt complex strategies to convert graphs into text sequences, resulting in significant token overhead and rendering them impractical for large-scale graphs. Others introduce additional modules to encode graphs into fixed-size token representations for LLMs. However, these methods typically require large-scale post-training on graph-text corpus and complex alignment procedures, yet often yield sub-optimal results due to poor modality alignment. Inspired by in-parameter knowledge injection for test-time adaptation of LLMs, we propose GRIP, a novel framework that equips LLMs with the ability to internalize complex relational information from graphs through carefully designed fine-tuning tasks. This knowledge is efficiently stored within lightweight LoRA parameters, enabling the fine-tuned LLM to perform a wide range of graph-related tasks without requiring access to the original graph at inference time. Extensive experiments across multiple benchmarks validate the effectiveness and efficiency of our approach.

LooGLE v2: Are LLMs Ready for Real World Long Dependency Challenges?

Large language models (LLMs) are equipped with increasingly extended context windows recently, yet their long context understanding capabilities over long dependency tasks remain fundamentally limited and underexplored. This gap is especially significant in many real-world long-context applications that were rarely benchmarked. In this paper, we introduce LooGLE v2, a novel benchmark designed to evaluate LLMs' long context ability in real-world applications and scenarios. Our benchmark consists of automatically collected real-world long texts, ranging from 16k to 2M tokens, encompassing domains in law, finance, game and code. Accordingly, we delicately design 10 types of domain-specific long-dependency tasks and generate 1,934 QA instances with various diversity and complexity in a scalable data curation pipeline for further practical needs. We conduct a comprehensive assessment of 6 locally deployed and 4 API-based LLMs. The evaluation results show that even the best-performing model achieves only a 59.2% overall score on our benchmark. Despite the extensive context windows, popular LLMs are only capable of understanding a much shorter length of context than they claim to be, revealing significant limitations in their ability to handle real-world tasks with long dependencies and highlighting substantial room for model improvement in practical long-context understanding.

GILT: An LLM-Free, Tuning-Free Graph Foundational Model for In-Context Learning

Graph Neural Networks (GNNs) are powerful tools for precessing relational data but often struggle to generalize to unseen graphs, giving rise to the development of Graph Foundational Models (GFMs). However, current GFMs are challenged by the extreme heterogeneity of graph data, where each graph can possess a unique feature space, label set, and topology. To address this, two main paradigms have emerged. The first leverages Large Language Models (LLMs), but is fundamentally text-dependent, thus struggles to handle the numerical features in vast graphs. The second pre-trains a structure-based model, but the adaptation to new tasks typically requires a costly, per-graph tuning stage, creating a critical efficiency bottleneck. In this work, we move beyond these limitations and introduce \textbf{G}raph \textbf{I}n-context \textbf{L}earning \textbf{T}ransformer (GILT), a framework built on an LLM-free and tuning-free architecture. GILT introduces a novel token-based framework for in-context learning (ICL) on graphs, reframing classification tasks spanning node, edge and graph levels in a unified framework. This mechanism is the key to handling heterogeneity, as it is designed to operate on generic numerical features. Further, its ability to understand class semantics dynamically from the context enables tuning-free adaptation. Comprehensive experiments show that GILT achieves stronger few-shot performance with significantly less time than LLM-based or tuning-based baselines, validating the effectiveness of our approach.

Round-trip Reinforcement Learning: Self-Consistent Training for Better Chemical LLMs

Large Language Models (LLMs) are emerging as versatile foundation models for computational chemistry, handling bidirectional tasks like reaction prediction and retrosynthesis. However, these models often lack round-trip consistency. For instance, a state-of-the-art chemical LLM may successfully caption a molecule, yet be unable to accurately reconstruct the original structure from its own generated text. This inconsistency suggests that models are learning unidirectional memorization rather than flexible mastery. Indeed, recent work has demonstrated a strong correlation between a model's round-trip consistency and its performance on the primary tasks. This strong correlation reframes consistency into a direct target for model improvement. We therefore introduce Round-Trip Reinforcement Learning (RTRL), a novel framework that trains a model to improve its consistency by using the success of a round-trip transformation as a reward signal. We further propose an iterative variant where forward and reverse mappings alternately train each other in a self-improvement loop, a process that is highly data-efficient and notably effective with the massive amount of unlabelled data common in chemistry. Experiments demonstrate that RTRL significantly \textbf{boosts performance and consistency} over strong baselines across supervised, self-supervised, and synthetic data regimes. This work shows that round-trip consistency is not just a desirable property but a trainable objective, offering a new path toward more robust and reliable foundation models.

GeoRecon: Graph-Level Representation Learning for 3D Molecules via Reconstruction-Based Pretraining

The pretraining-and-finetuning paradigm has driven significant advances across domains, such as natural language processing and computer vision, with representative pretraining paradigms such as masked language modeling and next-token prediction. However, in molecular representation learning, the task design remains largely limited to node-level denoising, which is effective at modeling local atomic environments, yet maybe insufficient for capturing the global molecular structure required by graph-level property prediction tasks, such as energy estimation and molecular regression. In this work, we present GeoRecon, a novel graph-level pretraining framework that shifts the focus from individual atoms to the molecule as an integrated whole. GeoRecon introduces a graph-level reconstruction task: during pretraining, the model is trained to generate an informative graph representation capable of accurately guiding reconstruction of the molecular geometry. This encourages the model to learn coherent, global structural features rather than isolated atomic details. Without relying on additional supervision or external data, GeoRecon outperforms node-centric baselines on multiple molecular benchmarks (e.g., QM9, MD17), demonstrating the benefit of incorporating graph-level reconstruction for learning more holistic and geometry-aware molecular embeddings.

Masked Language Models are Good Heterogeneous Graph Generalizers

Heterogeneous graph neural networks (HGNNs) excel at capturing structural and semantic information in heterogeneous graphs (HGs), while struggling to generalize across domains and tasks. Recently, some researchers have turned to integrating HGNNs with large language models (LLMs) for more generalizable heterogeneous graph learning. However, these approaches typically extract structural information via HGNNs as HG tokens, and disparities in embedding spaces between HGNNs and LLMs have been shown to bias the LLM's comprehension of HGs. Moreover, as these HG tokens are often derived from node-level tasks, the model's ability to generalize across tasks remains limited. To this end, we propose a simple yet effective Masked Language Modeling-based method, called MLM4HG. MLM4HG introduces metapath-based textual sequences instead of HG tokens to extract structural and semantic information inherent in HGs, and designs customized textual templates to unify different graph tasks into a coherent cloze-style "mask" token prediction paradigm. Specifically, MLM4HG first converts HGs from various domains to texts based on metapaths, and subsequently combines them with the unified task texts to form a HG-based corpus. Moreover, the corpus is fed into a pretrained LM for fine-tuning with a constrained target vocabulary, enabling the fine-tuned LM to generalize to unseen target HGs. Extensive cross-domain and multi-task experiments on four real-world datasets demonstrate the superior generalization performance of MLM4HG over state-of-the-art methods in both few-shot and zero-shot scenarios. Our code is available at https://github.com/BUPT-GAMMA/MLM4HG.

OCN: Effectively Utilizing Higher-Order Common Neighbors for Better Link Prediction

Common Neighbors (CNs) and their higher-order variants are important pairwise features widely used in state-of-the-art link prediction methods. However, existing methods often struggle with the repetition across different orders of CNs and fail to fully leverage their potential. We identify that these limitations stem from two key issues: redundancy and over-smoothing in high-order common neighbors. To address these challenges, we design orthogonalization to eliminate redundancy between different-order CNs and normalization to mitigate over-smoothing. By combining these two techniques, we propose Orthogonal Common Neighbor (OCN), a novel approach that significantly outperforms the strongest baselines by an average of 7.7% on popular link prediction benchmarks. A thorough theoretical analysis is provided to support our method. Ablation studies also verify the effectiveness of our orthogonalization and normalization techniques.

HD-PiSSA: High-Rank Distributed Orthogonal Adaptation

Existing parameter-efficient fine-tuning (PEFT) methods for large language models (LLMs), such as LoRA and PiSSA, constrain model updates to low-rank subspaces, limiting their expressiveness and leading to suboptimal performance on complex tasks. To address this, we introduce High-rank Distributed PiSSA (HD-PiSSA), a distributed PEFT approach that initializes orthogonal adapters across different devices and aggregates their delta updates collectively on W for fine-tuning. Unlike Data Parallel LoRA or PiSSA, which maintain identical adapters across all devices, HD-PiSSA assigns different principal components of the pre-trained weights to each GPU, significantly expanding the range of update directions. This results in over 16x higher effective updated ranks than data-parallel LoRA or PiSSA when fine-tuning on 8 GPUs with the same per-device adapter rank. Empirically, we evaluate HD-PiSSA across various challenging downstream tasks, including mathematics, code generation, and multi-task learning. In the multi-task setting, HD-PiSSA achieves average gains of 10.0 absolute points (14.63%) over LoRA and 4.98 points (6.60%) over PiSSA across 12 benchmarks, demonstrating its benefits from the extra optimization flexibility.