Local Causal Discovery with Background Knowledge

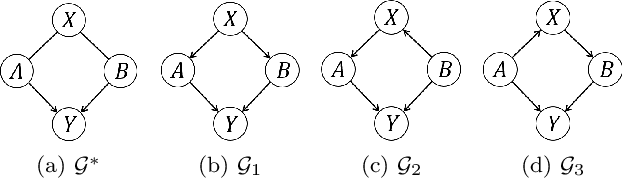
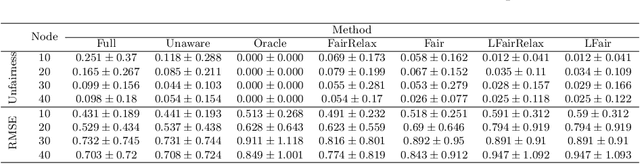
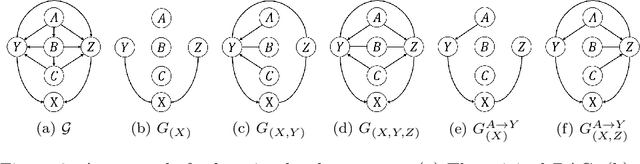
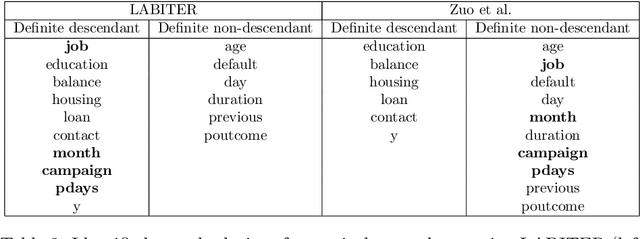
Causality plays a pivotal role in various fields of study. Based on the framework of causal graphical models, previous works have proposed identifying whether a variable is a cause or non-cause of a target in every Markov equivalent graph solely by learning a local structure. However, the presence of prior knowledge, often represented as a partially known causal graph, is common in many causal modeling applications. Leveraging this prior knowledge allows for the further identification of causal relationships. In this paper, we first propose a method for learning the local structure using all types of causal background knowledge, including direct causal information, non-ancestral information and ancestral information. Then we introduce criteria for identifying causal relationships based solely on the local structure in the presence of prior knowledge. We also apply out method to fair machine learning, and experiments involving local structure learning, causal relationship identification, and fair machine learning demonstrate that our method is both effective and efficient.

On the Representation of Causal Background Knowledge and its Applications in Causal Inference

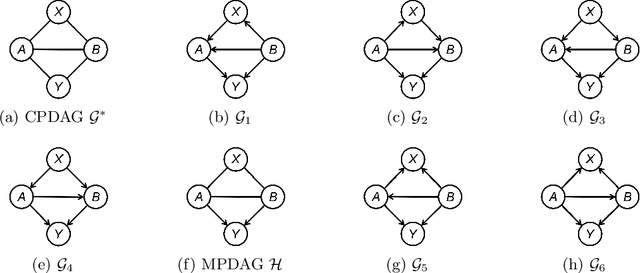
Causal background knowledge about the existence or the absence of causal edges and paths is frequently encountered in observational studies. The shared directed edges and links of a subclass of Markov equivalent DAGs refined due to background knowledge can be represented by a causal maximally partially directed acyclic graph (MPDAG). In this paper, we first provide a sound and complete graphical characterization of causal MPDAGs and give a minimal representation of a causal MPDAG. Then, we introduce a novel representation called direct causal clause (DCC) to represent all types of causal background knowledge in a unified form. Using DCCs, we study the consistency and equivalency of causal background knowledge and show that any causal background knowledge set can be equivalently decomposed into a causal MPDAG plus a minimal residual set of DCCs. Polynomial-time algorithms are also provided for checking the consistency, equivalency, and finding the decomposed MPDAG and residual DCCs. Finally, with causal background knowledge, we prove a sufficient and necessary condition to identify causal effects and surprisingly find that the identifiability of causal effects only depends on the decomposed MPDAG. We also develop a local IDA-type algorithm to estimate the possible values of an unidentifiable effect. Simulations suggest that causal background knowledge can significantly improve the identifiability of causal effects.

A Local Method for Identifying Causal Relations under Markov Equivalence

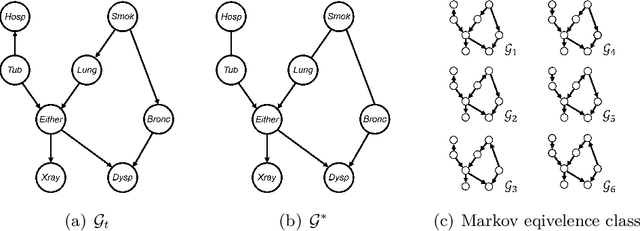
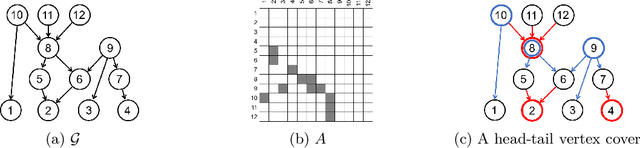
Causality is important for designing interpretable and robust methods in artificial intelligence research. We propose a local approach to identify whether a variable is a cause of a given target based on causal graphical models of directed acyclic graphs (DAGs). In general, the causal relation between two variables may not be identifiable from observational data as many causal DAGs encoding different causal relations are Markov equivalent. In this paper, we first introduce a sufficient and necessary graphical condition to check the existence of a causal path from a variable to a target in every Markov equivalent DAG. Next, we provide local criteria for identifying whether the variable is a cause/non-cause of the target. Finally, we propose a local learning algorithm for this causal query via learning local structure of the variable and some additional statistical independence tests related to the target. Simulation studies show that our local algorithm is efficient and effective, compared with other state-of-art methods.

Low Rank Directed Acyclic Graphs and Causal Structure Learning

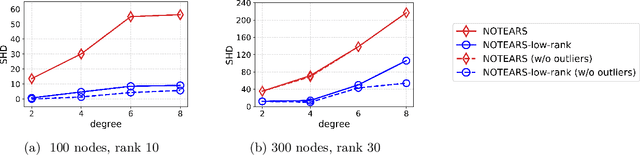
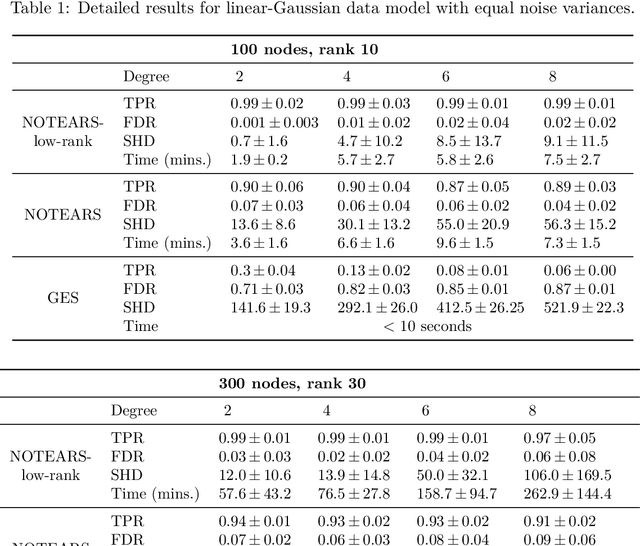
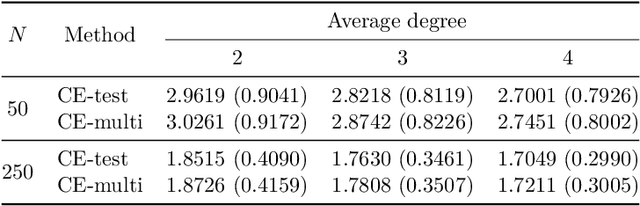
Despite several important advances in recent years, learning causal structures represented by directed acyclic graphs (DAGs) remains a challenging task in high dimensional settings when the graphs to be learned are not sparse. In particular, the recent formulation of structure learning as a continuous optimization problem proved to have considerable advantages over the traditional combinatorial formulation, but the performance of the resulting algorithms is still wanting when the target graph is relatively large and dense. In this paper we propose a novel approach to mitigate this problem, by exploiting a low rank assumption regarding the (weighted) adjacency matrix of a DAG causal model. We establish several useful results relating interpretable graphical conditions to the low rank assumption, and show how to adapt existing methods for causal structure learning to take advantage of this assumption. We also provide empirical evidence for the utility of our low rank algorithms, especially on graphs that are not sparse. Not only do they outperform state-of-the-art algorithms when the low rank condition is satisfied, the performance on randomly generated scale-free graphs is also very competitive even though the true ranks may not be as low as is assumed.

Formulas for Counting the Sizes of Markov Equivalence Classes of Directed Acyclic Graphs

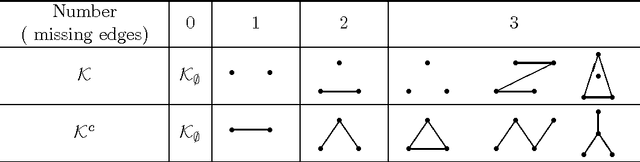
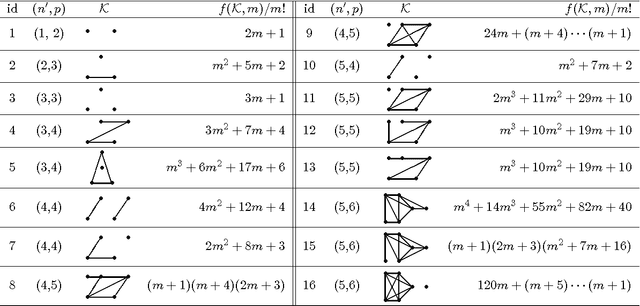
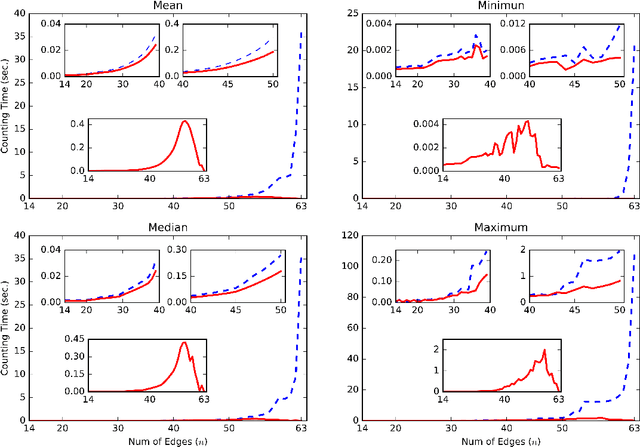
The sizes of Markov equivalence classes of directed acyclic graphs play important roles in measuring the uncertainty and complexity in causal learning. A Markov equivalence class can be represented by an essential graph and its undirected subgraphs determine the size of the class. In this paper, we develop a method to derive the formulas for counting the sizes of Markov equivalence classes. We first introduce a new concept of core graph. The size of a Markov equivalence class of interest is a polynomial of the number of vertices given its core graph. Then, we discuss the recursive and explicit formula of the polynomial, and provide an algorithm to derive the size formula via symbolic computation for any given core graph. The proposed size formula derivation sheds light on the relationships between the size of a Markov equivalence class and its representation graph, and makes size counting efficient, even when the essential graphs contain non-sparse undirected subgraphs.

Reversible MCMC on Markov equivalence classes of sparse directed acyclic graphs

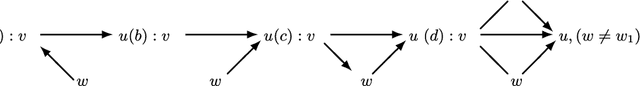
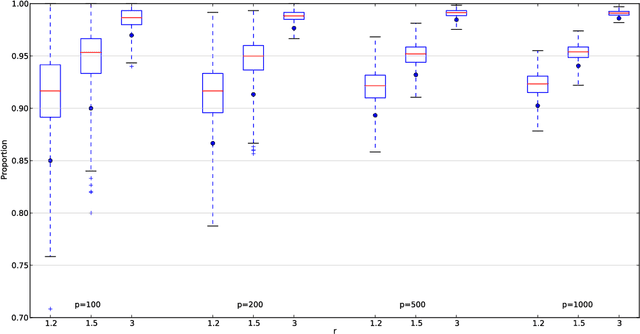
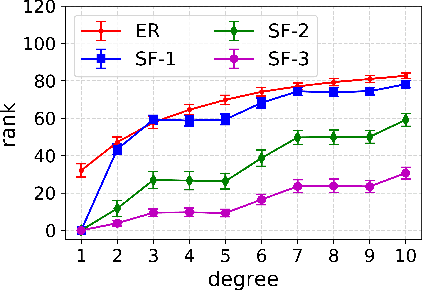
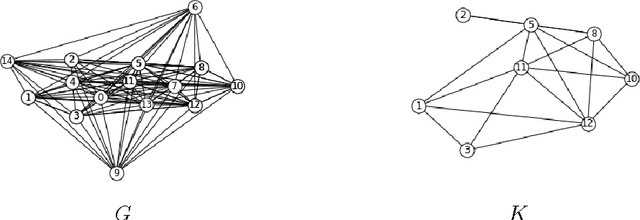
Graphical models are popular statistical tools which are used to represent dependent or causal complex systems. Statistically equivalent causal or directed graphical models are said to belong to a Markov equivalent class. It is of great interest to describe and understand the space of such classes. However, with currently known algorithms, sampling over such classes is only feasible for graphs with fewer than approximately 20 vertices. In this paper, we design reversible irreducible Markov chains on the space of Markov equivalent classes by proposing a perfect set of operators that determine the transitions of the Markov chain. The stationary distribution of a proposed Markov chain has a closed form and can be computed easily. Specifically, we construct a concrete perfect set of operators on sparse Markov equivalence classes by introducing appropriate conditions on each possible operator. Algorithms and their accelerated versions are provided to efficiently generate Markov chains and to explore properties of Markov equivalence classes of sparse directed acyclic graphs (DAGs) with thousands of vertices. We find experimentally that in most Markov equivalence classes of sparse DAGs, (1) most edges are directed, (2) most undirected subgraphs are small and (3) the number of these undirected subgraphs grows approximately linearly with the number of vertices. The article contains supplement arXiv:1303.0632, http://dx.doi.org/10.1214/13-AOS1125SUPP

Supplement to "Reversible MCMC on Markov equivalence classes of sparse directed acyclic graphs"

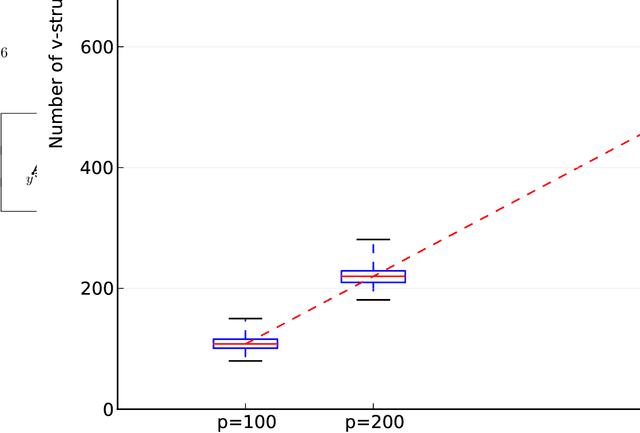
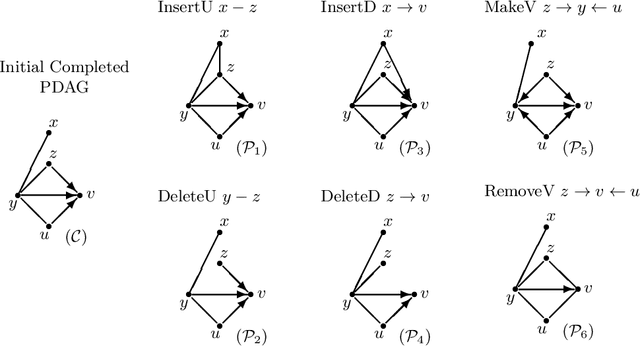
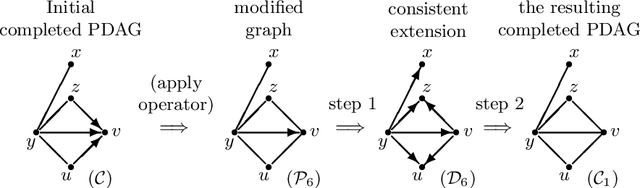
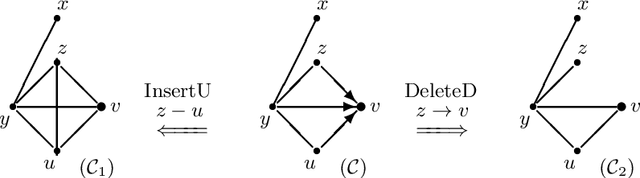
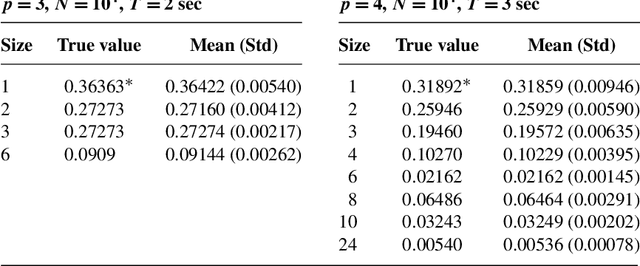
This supplementary material includes three parts: some preliminary results, four examples, an experiment, three new algorithms, and all proofs of the results in the paper "Reversible MCMC on Markov equivalence classes of sparse directed acyclic graphs".