Zhouchen Lin
MorphoBench: A Benchmark with Difficulty Adaptive to Model Reasoning
Oct 16, 2025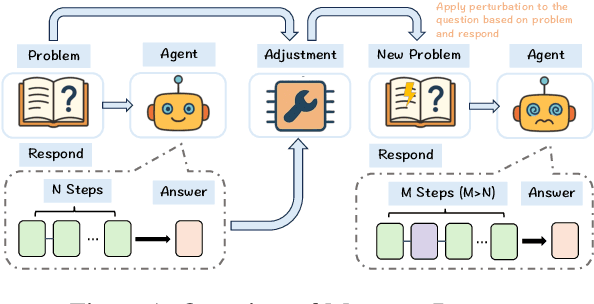

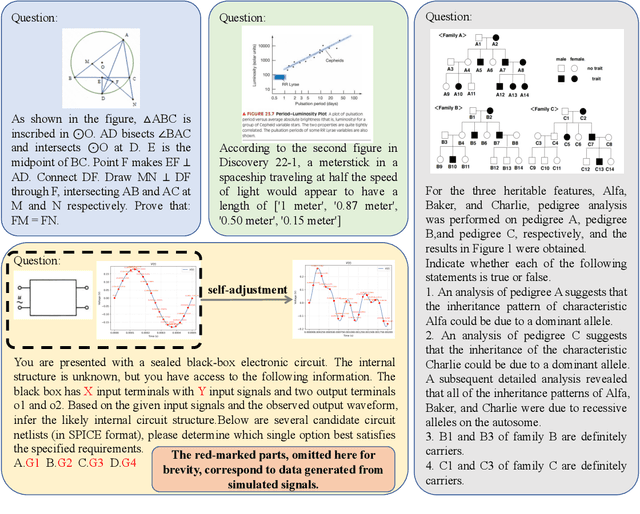
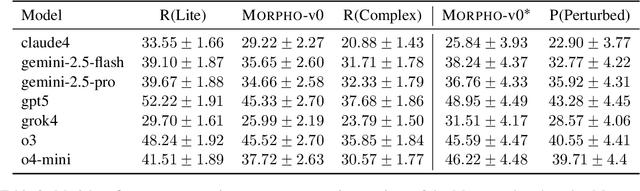
Abstract:With the advancement of powerful large-scale reasoning models, effectively evaluating the reasoning capabilities of these models has become increasingly important. However, existing benchmarks designed to assess the reasoning abilities of large models tend to be limited in scope and lack the flexibility to adapt their difficulty according to the evolving reasoning capacities of the models. To address this, we propose MorphoBench, a benchmark that incorporates multidisciplinary questions to evaluate the reasoning capabilities of large models and can adjust and update question difficulty based on the reasoning abilities of advanced models. Specifically, we curate the benchmark by selecting and collecting complex reasoning questions from existing benchmarks and sources such as Olympiad-level competitions. Additionally, MorphoBench adaptively modifies the analytical challenge of questions by leveraging key statements generated during the model's reasoning process. Furthermore, it includes questions generated using simulation software, enabling dynamic adjustment of benchmark difficulty with minimal resource consumption. We have gathered over 1,300 test questions and iteratively adjusted the difficulty of MorphoBench based on the reasoning capabilities of models such as o3 and GPT-5. MorphoBench enhances the comprehensiveness and validity of model reasoning evaluation, providing reliable guidance for improving both the reasoning abilities and scientific robustness of large models. The code has been released in https://github.com/OpenDCAI/MorphoBench.
Explicit Discovery of Nonlinear Symmetries from Dynamic Data
Oct 02, 2025Abstract:Symmetry is widely applied in problems such as the design of equivariant networks and the discovery of governing equations, but in complex scenarios, it is not known in advance. Most previous symmetry discovery methods are limited to linear symmetries, and recent attempts to discover nonlinear symmetries fail to explicitly get the Lie algebra subspace. In this paper, we propose LieNLSD, which is, to our knowledge, the first method capable of determining the number of infinitesimal generators with nonlinear terms and their explicit expressions. We specify a function library for the infinitesimal group action and aim to solve for its coefficient matrix, proving that its prolongation formula for differential equations, which governs dynamic data, is also linear with respect to the coefficient matrix. By substituting the central differences of the data and the Jacobian matrix of the trained neural network into the infinitesimal criterion, we get a system of linear equations for the coefficient matrix, which can then be solved using SVD. On top quark tagging and a series of dynamic systems, LieNLSD shows qualitative advantages over existing methods and improves the long rollout accuracy of neural PDE solvers by over 20% while applying to guide data augmentation. Code and data are available at https://github.com/hulx2002/LieNLSD.
A Self-Ensemble Inspired Approach for Effective Training of Binary-Weight Spiking Neural Networks
Aug 18, 2025Abstract:Spiking Neural Networks (SNNs) are a promising approach to low-power applications on neuromorphic hardware due to their energy efficiency. However, training SNNs is challenging because of the non-differentiable spike generation function. To address this issue, the commonly used approach is to adopt the backpropagation through time framework, while assigning the gradient of the non-differentiable function with some surrogates. Similarly, Binary Neural Networks (BNNs) also face the non-differentiability problem and rely on approximating gradients. However, the deep relationship between these two fields and how their training techniques can benefit each other has not been systematically researched. Furthermore, training binary-weight SNNs is even more difficult. In this work, we present a novel perspective on the dynamics of SNNs and their close connection to BNNs through an analysis of the backpropagation process. We demonstrate that training a feedforward SNN can be viewed as training a self-ensemble of a binary-activation neural network with noise injection. Drawing from this new understanding of SNN dynamics, we introduce the Self-Ensemble Inspired training method for (Binary-Weight) SNNs (SEI-BWSNN), which achieves high-performance results with low latency even for the case of the 1-bit weights. Specifically, we leverage a structure of multiple shortcuts and a knowledge distillation-based training technique to improve the training of (binary-weight) SNNs. Notably, by binarizing FFN layers in a Transformer architecture, our approach achieves 82.52% accuracy on ImageNet with only 2 time steps, indicating the effectiveness of our methodology and the potential of binary-weight SNNs.
DNT: a Deeply Normalized Transformer that can be trained by Momentum SGD
Jul 23, 2025Abstract:Transformers have become the de facto backbone of modern deep learning, yet their training typically demands an advanced optimizer with adaptive learning rate like AdamW, rather than a momentum SGDW (mSGDW). Previous works show that it is mainly due to a heavy-tailed distribution of the gradients. In this paper, we introduce a Deeply Normalized Transformer (DNT), which is meticulously engineered to overcome this limitation enabling seamless training with vanilla mSGDW while yielding comparable performance to the Transformers trained via AdamW. To be specific, in DNT, we strategically integrate normalization techniques at proper positions in the Transformers to effectively modulate the Jacobian matrices of each layer, balance the influence of weights, activations, and their interactions, and thus enable the distributions of gradients concentrated. We provide both theoretical justifications of the normalization technique used in our DNT and extensive empirical evaluation on two popular Transformer architectures to validate that: a) DNT outperforms its counterparts (\ie, ViT and GPT), and b) DNT can be effectively trained with vanilla mSGDW.
Stepsize anything: A unified learning rate schedule for budgeted-iteration training
May 30, 2025Abstract:The expanding computational costs and limited resources underscore the critical need for budgeted-iteration training, which aims to achieve optimal learning within predetermined iteration budgets.While learning rate schedules fundamentally govern the performance of different networks and tasks, particularly in budgeted-iteration scenarios, their design remains largely heuristic, lacking theoretical foundations.In addition, the optimal learning rate schedule requires extensive trial-and-error selection, making the training process inefficient.In this work, we propose the Unified Budget-Aware (UBA) schedule, a theoretically grounded learning rate schedule that consistently outperforms commonly-used schedules among diverse architectures and tasks under different constrained training budgets.First, we bridge the gap by constructing a novel training budget-aware optimization framework, which explicitly accounts for the robustness to landscape curvature variations.From this framework, we derive the UBA schedule, controlled by a single hyper-parameter $\varphi$ that provides a trade-off between flexibility and simplicity, eliminating the need for per-network numerical optimization. Moreover, we establish a theoretical connection between $\varphi$ and the condition number, adding interpretation and justification to our approach. Besides, we prove the convergence for different values of $\varphi$.We offer practical guidelines for its selection via theoretical analysis and empirical results.xtensive experimental results show that UBA \textit{consistently surpasses} the commonly-used schedules across diverse vision and language tasks, spanning network architectures (e.g., ResNet, OLMo) and scales, under different training-iteration budgets.
Governing Equation Discovery from Data Based on Differential Invariants
May 24, 2025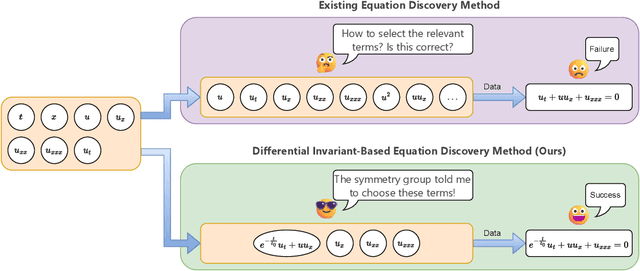

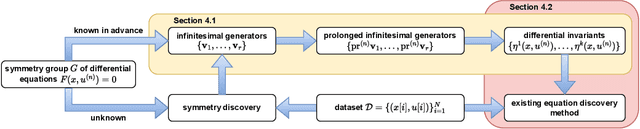
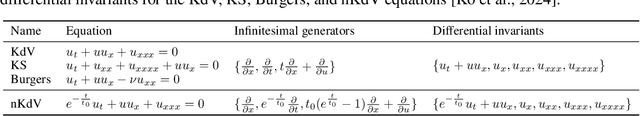
Abstract:The explicit governing equation is one of the simplest and most intuitive forms for characterizing physical laws. However, directly discovering partial differential equations (PDEs) from data poses significant challenges, primarily in determining relevant terms from a vast search space. Symmetry, as a crucial prior knowledge in scientific fields, has been widely applied in tasks such as designing equivariant networks and guiding neural PDE solvers. In this paper, we propose a pipeline for governing equation discovery based on differential invariants, which can losslessly reduce the search space of existing equation discovery methods while strictly adhering to symmetry. Specifically, we compute the set of differential invariants corresponding to the infinitesimal generators of the symmetry group and select them as the relevant terms for equation discovery. Taking DI-SINDy (SINDy based on Differential Invariants) as an example, we demonstrate that its success rate and accuracy in PDE discovery surpass those of other symmetry-informed governing equation discovery methods across a series of PDEs.
TransDF: Time-Series Forecasting Needs Transformed Label Alignment
May 23, 2025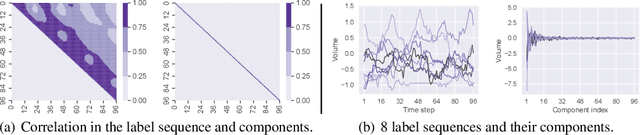
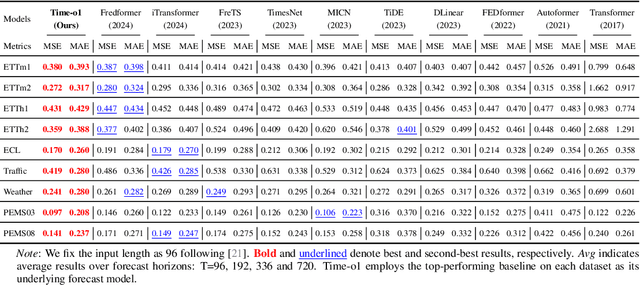
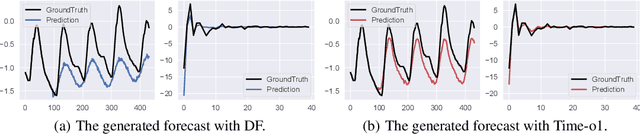
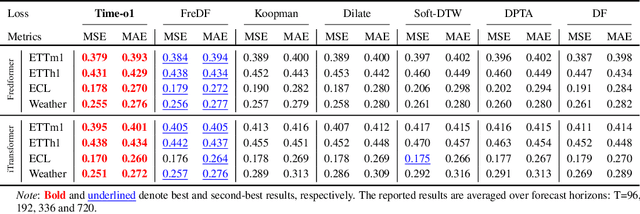
Abstract:Training time-series forecasting models presents unique challenges in designing effective learning objectives. Existing methods predominantly utilize the temporal mean squared error, which faces two critical challenges: (1) label autocorrelation, which leads to bias from the label sequence likelihood; (2) excessive amount of tasks, which increases with the forecast horizon and complicates optimization. To address these challenges, we propose Transform-enhanced Direct Forecast (TransDF), which transforms the label sequence into decorrelated components with discriminated significance. Models are trained to align the most significant components, thereby effectively mitigating label autocorrelation and reducing task amount. Extensive experiments demonstrate that TransDF achieves state-of-the-art performance and is compatible with various forecasting models. Code is available at https://anonymous.4open.science/r/TransDF-88CF.
On the $O(\frac{\sqrt{d}}{K^{1/4}})$ Convergence Rate of AdamW Measured by $\ell_1$ Norm
May 17, 2025Abstract:As the default optimizer for training large language models, AdamW has achieved remarkable success in deep learning. However, its convergence behavior is not theoretically well-understood. This paper establishes the convergence rate $\frac{1}{K}\sum_{k=1}^KE\left[\|\nabla f(x^k)\|_1\right]\leq O(\frac{\sqrt{d}C}{K^{1/4}})$ for AdamW measured by $\ell_1$ norm, where $K$ represents the iteration number, $d$ denotes the model dimension, and $C$ matches the constant in the optimal convergence rate of SGD. Theoretically, we have $E\left[\|\nabla f(x)\|_1\right]\geq\sqrt{\frac{2d}{\pi}}E\left[\|\nabla f(x)\|_2\right]$ when each element of $\nabla f(x)$ is generated from Gaussian distribution $\mathcal N(0,1)$. Empirically, our experimental results on real-world deep learning tasks reveal $\|\nabla f(x)\|_1=\varTheta(\sqrt{d})\|\nabla f(x)\|_2$. Both support that our convergence rate can be considered to be analogous to the optimal $\frac{1}{K}\sum_{k=1}^KE\left[\|\nabla f(x^k)\|_2\right]\leq O(\frac{C}{K^{1/4}})$ convergence rate of SGD.
VACT: A Video Automatic Causal Testing System and a Benchmark
Mar 08, 2025Abstract:With the rapid advancement of text-conditioned Video Generation Models (VGMs), the quality of generated videos has significantly improved, bringing these models closer to functioning as ``*world simulators*'' and making real-world-level video generation more accessible and cost-effective. However, the generated videos often contain factual inaccuracies and lack understanding of fundamental physical laws. While some previous studies have highlighted this issue in limited domains through manual analysis, a comprehensive solution has not yet been established, primarily due to the absence of a generalized, automated approach for modeling and assessing the causal reasoning of these models across diverse scenarios. To address this gap, we propose VACT: an **automated** framework for modeling, evaluating, and measuring the causal understanding of VGMs in real-world scenarios. By combining causal analysis techniques with a carefully designed large language model assistant, our system can assess the causal behavior of models in various contexts without human annotation, which offers strong generalization and scalability. Additionally, we introduce multi-level causal evaluation metrics to provide a detailed analysis of the causal performance of VGMs. As a demonstration, we use our framework to benchmark several prevailing VGMs, offering insight into their causal reasoning capabilities. Our work lays the foundation for systematically addressing the causal understanding deficiencies in VGMs and contributes to advancing their reliability and real-world applicability.
Empowering LLMs with Logical Reasoning: A Comprehensive Survey
Feb 21, 2025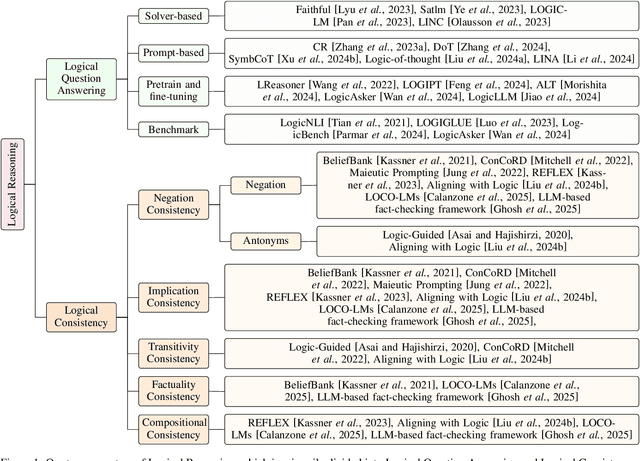
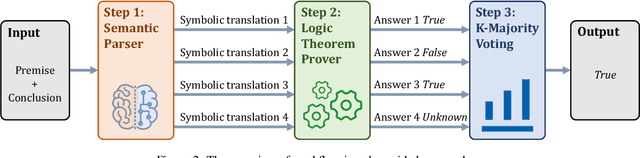
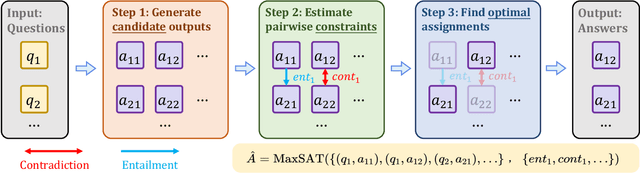
Abstract:Large language models (LLMs) have achieved remarkable successes on various natural language tasks. However, recent studies have found that there are still significant challenges to the logical reasoning abilities of LLMs. This paper summarizes and categorizes the main challenges into two aspects: (1) Logical question answering, LLMs often fail to generate the correct answer within complex logical problem which requires sophisticated deductive, inductive or abductive reasoning given a collection of premises and constrains. (2) Logical consistency, LLMs are prone to producing responses contradicting themselves across different questions. For example, a state-of-the-art Macaw question-answering LLM answers Yes to both questions Is a magpie a bird? and Does a bird have wings? but answers No to Does a magpie have wings?. To facilitate this research direction, we comprehensively investigate the most cutting-edge methods and propose detailed taxonomies of these methods. Specifically, to accurately answer complex logic questions, previous methods can be categorized based on reliance on external solvers, prompts, pretraining, and fine-tuning. To avoid logical contradictions, we discuss concepts and solutions of various logical consistencies, including implication, negation, transitivity, factuality consistency, and their composites. In addition, we review commonly used benchmark datasets and evaluation metrics, and discuss promising research directions, such as extensions to modal logic to account for uncertainty, and efficient algorithms satisfying multiple logical consistencies simultaneously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge