Ratio law: mathematical descriptions for a universal relationship between AI performance and input samples

Artificial intelligence based on machine learning and deep learning has made significant advances in various fields such as protein structure prediction and climate modeling. However, a central challenge remains: the "black box" nature of AI, where precise quantitative relationships between inputs and outputs are often lacking. Here, by analyzing 323 AI models trained to predict human essential proteins, we uncovered a ratio law showing that model performance and the ratio of minority to majority samples can be closely linked by two concise equations. Moreover, we mathematically proved that an AI model achieves its optimal performance on a balanced dataset. More importantly, we next explore whether this finding can further guide us to enhance AI models' performance. Therefore, we divided the imbalanced dataset into several balanced subsets to train base classifiers, and then applied a bagging-based ensemble learning strategy to combine these base models. As a result, the equation-guided strategy substantially improved model performance, with increases of 4.06% and 5.28%, respectively, outperforming traditional dataset balancing techniques. Finally, we confirmed the broad applicability and generalization of these equations using different types of classifiers and 10 additional, diverse binary classification tasks. In summary, this study reveals two equations precisely linking AI's input and output, which could be helpful for unboxing the mysterious "black box" of AI.

FreeCG: Free the Design Space of Clebsch-Gordan Transform for machine learning force field

The Clebsch-Gordan Transform (CG transform) effectively encodes many-body interactions. Many studies have proven its accuracy in depicting atomic environments, although this comes with high computational needs. The computational burden of this challenge is hard to reduce due to the need for permutation equivariance, which limits the design space of the CG transform layer. We show that, implementing the CG transform layer on permutation-invariant inputs allows complete freedom in the design of this layer without affecting symmetry. Developing further on this premise, our idea is to create a CG transform layer that operates on permutation-invariant abstract edges generated from real edge information. We bring in group CG transform with sparse path, abstract edges shuffling, and attention enhancer to form a powerful and efficient CG transform layer. Our method, known as FreeCG, achieves State-of-The-Art (SoTA) results in force prediction for MD17, rMD17, MD22, and property prediction in QM9 datasets with notable enhancement. It introduces a novel paradigm for carrying out efficient and expressive CG transform in future geometric neural network designs.

Global Features are All You Need for Image Retrieval and Reranking

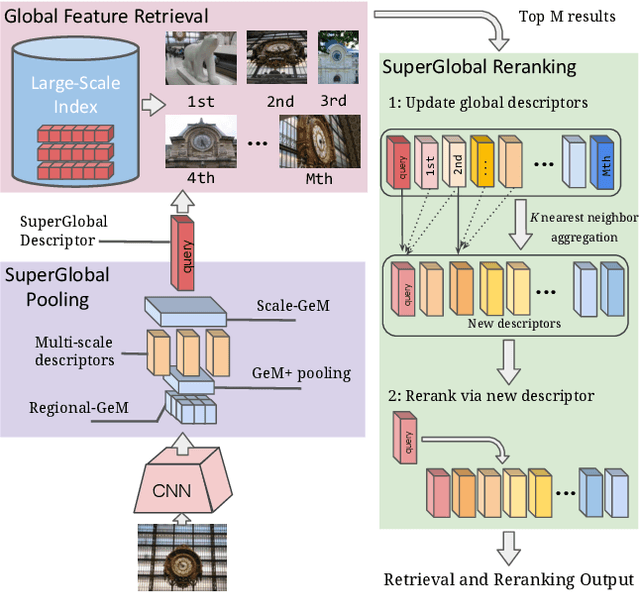
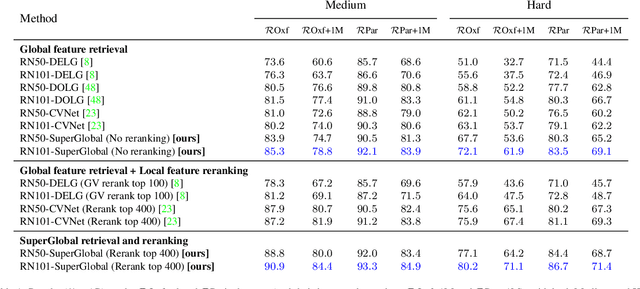
Image retrieval systems conventionally use a two-stage paradigm, leveraging global features for initial retrieval and local features for reranking. However, the scalability of this method is often limited due to the significant storage and computation cost incurred by local feature matching in the reranking stage. In this paper, we present SuperGlobal, a novel approach that exclusively employs global features for both stages, improving efficiency without sacrificing accuracy. SuperGlobal introduces key enhancements to the retrieval system, specifically focusing on the global feature extraction and reranking processes. For extraction, we identify sub-optimal performance when the widely-used ArcFace loss and Generalized Mean (GeM) pooling methods are combined and propose several new modules to improve GeM pooling. In the reranking stage, we introduce a novel method to update the global features of the query and top-ranked images by only considering feature refinement with a small set of images, thus being very compute and memory efficient. Our experiments demonstrate substantial improvements compared to the state of the art in standard benchmarks. Notably, on the Revisited Oxford+1M Hard dataset, our single-stage results improve by 7.1%, while our two-stage gain reaches 3.7% with a strong 64,865x speedup. Our two-stage system surpasses the current single-stage state-of-the-art by 16.3%, offering a scalable, accurate alternative for high-performing image retrieval systems with minimal time overhead. Code: https://github.com/ShihaoShao-GH/SuperGlobal.

1st Place Solution in Google Universal Images Embedding

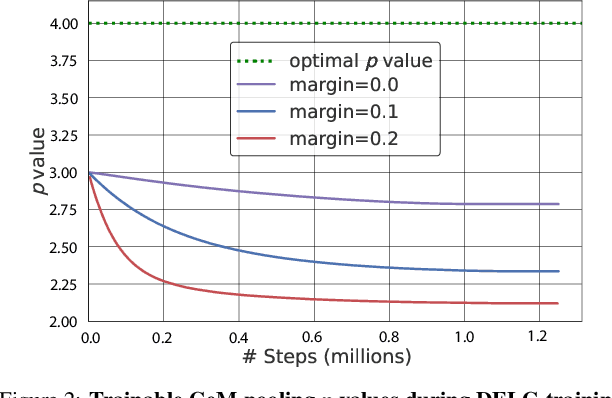
This paper presents the 1st place solution for the Google Universal Images Embedding Competition on Kaggle. The highlighted part of our solution is based on 1) A novel way to conduct training and fine-tuning; 2) The idea of a better ensemble in the pool of models that make embedding; 3) The potential trade-off between fine-tuning on high-resolution and overlapping patches; 4) The potential factors to work for the dynamic margin. Our solution reaches 0.728 in the private leader board, which achieve 1st place in Google Universal Images Embedding Competition.

A layer-stress learning framework universally augments deep neural network tasks

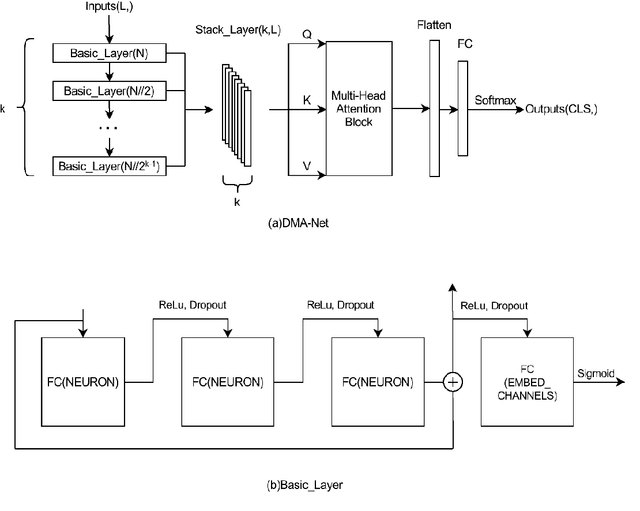
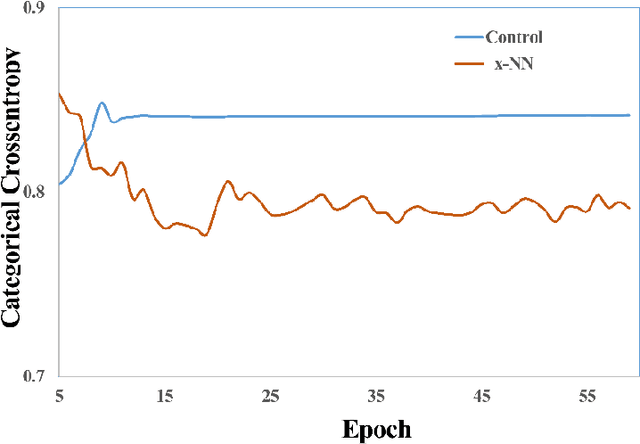
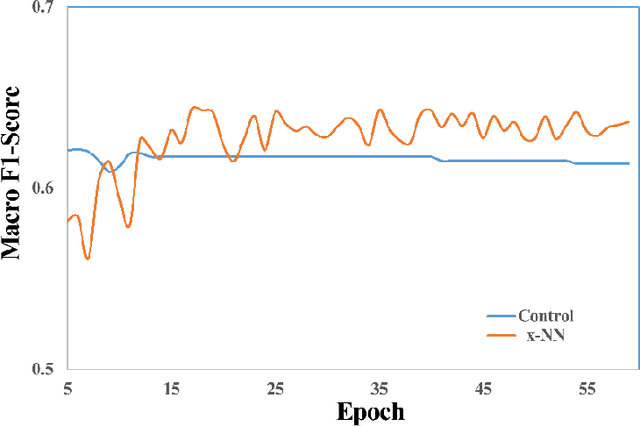
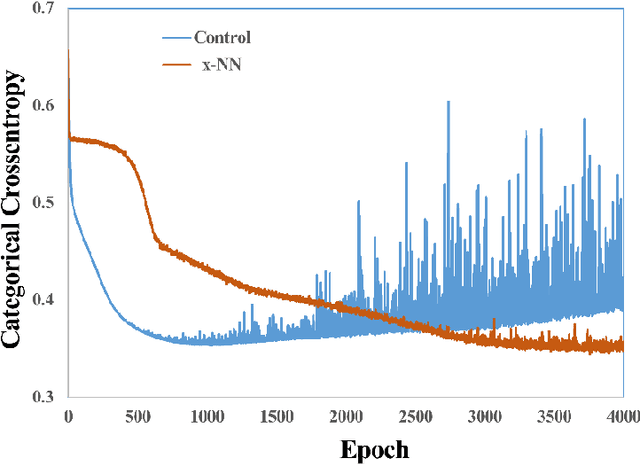
Deep neural networks (DNN) such as Multi-Layer Perception (MLP) and Convolutional Neural Networks (CNN) represent one of the most established deep learning algorithms. Given the tremendous effects of the number of hidden layers on network architecture and performance, it is very important to choose the number of hidden layers but still a serious challenge. More importantly, the current network architectures can only process the information from the last layer of the feature extractor, which greatly limited us to further improve its performance. Here we presented a layer-stress deep learning framework (x-NN) which implemented automatic and wise depth decision on shallow or deep feature map in a deep network through firstly designing enough number of layers and then trading off them by Multi-Head Attention Block. The x-NN can make use of features from various depth layers through attention allocation and then help to make final decision as well. As a result, x-NN showed outstanding prediction ability in the Alzheimer's Disease Classification Technique Challenge PRCV 2021, in which it won the top laurel and outperformed all other AI models. Moreover, the performance of x-NN was verified by one more AD neuroimaging dataset and other AI tasks.