Learning Design-Score Manifold to Guide Diffusion Models for Offline Optimization

Optimizing complex systems, from discovering therapeutic drugs to designing high-performance materials, remains a fundamental challenge across science and engineering, as the underlying rules are often unknown and costly to evaluate. Offline optimization aims to optimize designs for target scores using pre-collected datasets without system interaction. However, conventional approaches may fail beyond training data, predicting inaccurate scores and generating inferior designs. This paper introduces ManGO, a diffusion-based framework that learns the design-score manifold, capturing the design-score interdependencies holistically. Unlike existing methods that treat design and score spaces in isolation, ManGO unifies forward prediction and backward generation, attaining generalization beyond training data. Key to this is its derivative-free guidance for conditional generation, coupled with adaptive inference-time scaling that dynamically optimizes denoising paths. Extensive evaluations demonstrate that ManGO outperforms 24 single- and 10 multi-objective optimization methods across diverse domains, including synthetic tasks, robot control, material design, DNA sequence, and real-world engineering optimization.

Proximalized Preference Optimization for Diverse Feedback Types: A Decomposed Perspective on DPO

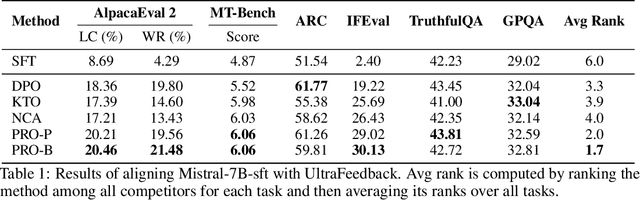
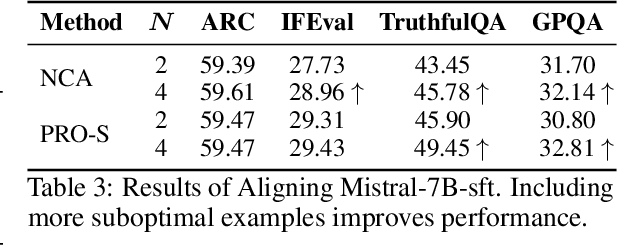
Direct alignment methods typically optimize large language models (LLMs) by contrasting the likelihoods of preferred versus dispreferred responses. While effective in steering LLMs to match relative preference, these methods are frequently noted for decreasing the absolute likelihoods of example responses. As a result, aligned models tend to generate outputs that deviate from the expected patterns, exhibiting reward-hacking effect even without a reward model. This undesired consequence exposes a fundamental limitation in contrastive alignment, which we characterize as likelihood underdetermination. In this work, we revisit direct preference optimization (DPO) -- the seminal direct alignment method -- and demonstrate that its loss theoretically admits a decomposed reformulation. The reformulated loss not only broadens applicability to a wider range of feedback types, but also provides novel insights into the underlying cause of likelihood underdetermination. Specifically, the standard DPO implementation implicitly oversimplifies a regularizer in the reformulated loss, and reinstating its complete version effectively resolves the underdetermination issue. Leveraging these findings, we introduce PRoximalized PReference Optimization (PRO), a unified method to align with diverse feeback types, eliminating likelihood underdetermination through an efficient approximation of the complete regularizer. Comprehensive experiments show the superiority of PRO over existing methods in scenarios involving pairwise, binary and scalar feedback.

Generative Models in Decision Making: A Survey

In recent years, the exceptional performance of generative models in generative tasks has sparked significant interest in their integration into decision-making processes. Due to their ability to handle complex data distributions and their strong model capacity, generative models can be effectively incorporated into decision-making systems by generating trajectories that guide agents toward high-reward state-action regions or intermediate sub-goals. This paper presents a comprehensive review of the application of generative models in decision-making tasks. We classify seven fundamental types of generative models: energy-based models, generative adversarial networks, variational autoencoders, normalizing flows, diffusion models, generative flow networks, and autoregressive models. Regarding their applications, we categorize their functions into three main roles: controllers, modelers and optimizers, and discuss how each role contributes to decision-making. Furthermore, we examine the deployment of these models across five critical real-world decision-making scenarios. Finally, we summarize the strengths and limitations of current approaches and propose three key directions for advancing next-generation generative directive models: high-performance algorithms, large-scale generalized decision-making models, and self-evolving and adaptive models.

Causal Coordinated Concurrent Reinforcement Learning

In this work, we propose a novel algorithmic framework for data sharing and coordinated exploration for the purpose of learning more data-efficient and better performing policies under a concurrent reinforcement learning (CRL) setting. In contrast to other work which make the assumption that all agents act under identical environments, we relax this restriction and instead consider the formulation where each agent acts within an environment which shares a global structure but also exhibits individual variations. Our algorithm leverages a causal inference algorithm in the form of Additive Noise Model - Mixture Model (ANM-MM) in extracting model parameters governing individual differentials via independence enforcement. We propose a new data sharing scheme based on a similarity measure of the extracted model parameters and demonstrate superior learning speeds on a set of autoregressive, pendulum and cart-pole swing-up tasks and finally, we show the effectiveness of diverse action selection between common agents under a sparse reward setting. To the best of our knowledge, this is the first work in considering non-identical environments in CRL and one of the few works which seek to integrate causal inference with reinforcement learning (RL).

Causal Discovery by Kernel Deviance Measures with Heterogeneous Transforms

The discovery of causal relationships in a set of random variables is a fundamental objective of science and has also recently been argued as being an essential component towards real machine intelligence. One class of causal discovery techniques are founded based on the argument that there are inherent structural asymmetries between the causal and anti-causal direction which could be leveraged in determining the direction of causation. To go about capturing these discrepancies between cause and effect remains to be a challenge and many current state-of-the-art algorithms propose to compare the norms of the kernel mean embeddings of the conditional distributions. In this work, we argue that such approaches based on RKHS embeddings are insufficient in capturing principal markers of cause-effect asymmetry involving higher-order structural variabilities of the conditional distributions. We propose Kernel Intrinsic Invariance Measure with Heterogeneous Transform (KIIM-HT) which introduces a novel score measure based on heterogeneous transformation of RKHS embeddings to extract relevant higher-order moments of the conditional densities for causal discovery. Inference is made via comparing the score of each hypothetical cause-effect direction. Tests and comparisons on a synthetic dataset, a two-dimensional synthetic dataset and the real-world benchmark dataset T\"ubingen Cause-Effect Pairs verify our approach. In addition, we conduct a sensitivity analysis to the regularization parameter to faithfully compare previous work to our method and an experiment with trials on varied hyperparameter values to showcase the robustness of our algorithm.

Efficient Robust Bayesian Optimization for Arbitrary Uncertain Inputs

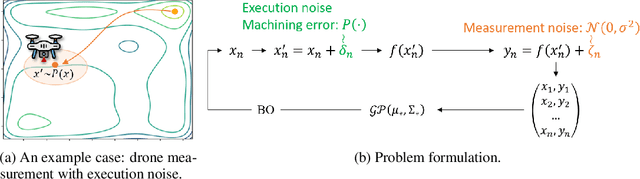
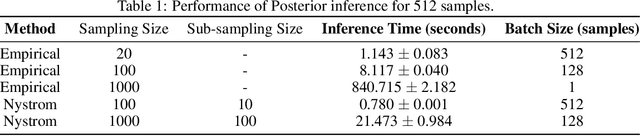
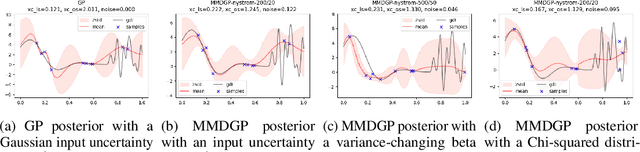
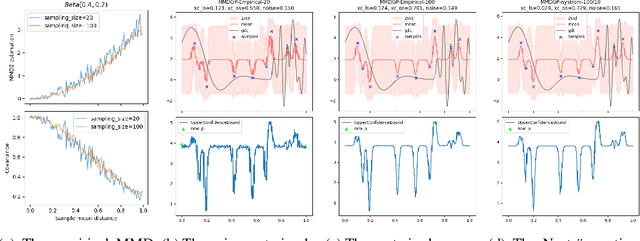
Bayesian Optimization (BO) is a sample-efficient optimization algorithm widely employed across various applications. In some challenging BO tasks, input uncertainty arises due to the inevitable randomness in the optimization process, such as machining errors, execution noise, or contextual variability. This uncertainty deviates the input from the intended value before evaluation, resulting in significant performance fluctuations in the final result. In this paper, we introduce a novel robust Bayesian Optimization algorithm, AIRBO, which can effectively identify a robust optimum that performs consistently well under arbitrary input uncertainty. Our method directly models the uncertain inputs of arbitrary distributions by empowering the Gaussian Process with the Maximum Mean Discrepancy (MMD) and further accelerates the posterior inference via Nystrom approximation. Rigorous theoretical regret bound is established under MMD estimation error and extensive experiments on synthetic functions and real problems demonstrate that our approach can handle various input uncertainties and achieve state-of-the-art performance.

Convergence guarantee for consistency models

We provide the first convergence guarantees for the Consistency Models (CMs), a newly emerging type of one-step generative models that can generate comparable samples to those generated by Diffusion Models. Our main result is that, under the basic assumptions on score-matching errors, consistency errors and smoothness of the data distribution, CMs can efficiently sample from any realistic data distribution in one step with small $W_2$ error. Our results (1) hold for $L^2$-accurate score and consistency assumption (rather than $L^\infty$-accurate); (2) do note require strong assumptions on the data distribution such as log-Sobelev inequality; (3) scale polynomially in all parameters; and (4) match the state-of-the-art convergence guarantee for score-based generative models (SGMs). We also provide the result that the Multistep Consistency Sampling procedure can further reduce the error comparing to one step sampling, which support the original statement of "Consistency Models, Yang Song 2023". Our result further imply a TV error guarantee when take some Langevin-based modifications to the output distributions.

Efficient Bayesian Optimization with Deep Kernel Learning and Transformer Pre-trained on Multiple Heterogeneous Datasets

Bayesian optimization (BO) is widely adopted in black-box optimization problems and it relies on a surrogate model to approximate the black-box response function. With the increasing number of black-box optimization tasks solved and even more to solve, the ability to learn from multiple prior tasks to jointly pre-train a surrogate model is long-awaited to further boost optimization efficiency. In this paper, we propose a simple approach to pre-train a surrogate, which is a Gaussian process (GP) with a kernel defined on deep features learned from a Transformer-based encoder, using datasets from prior tasks with possibly heterogeneous input spaces. In addition, we provide a simple yet effective mix-up initialization strategy for input tokens corresponding to unseen input variables and therefore accelerate new tasks' convergence. Experiments on both synthetic and real benchmark problems demonstrate the effectiveness of our proposed pre-training and transfer BO strategy over existing methods.

Reweighted Interacting Langevin Diffusions: an Accelerated Sampling Methodfor Optimization

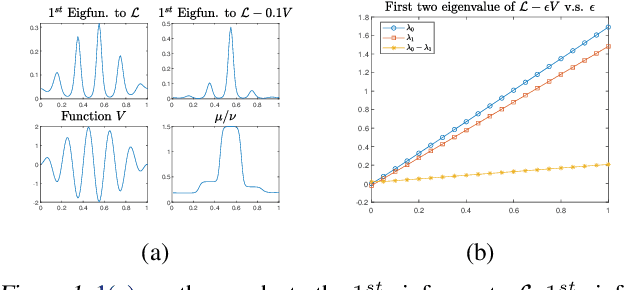
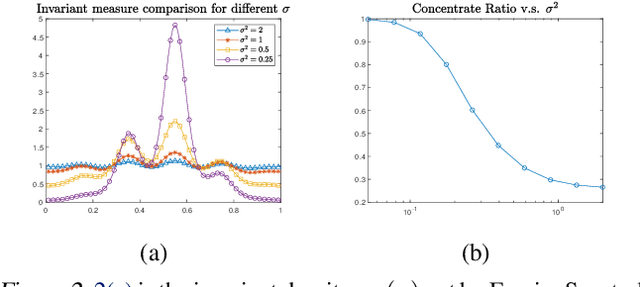
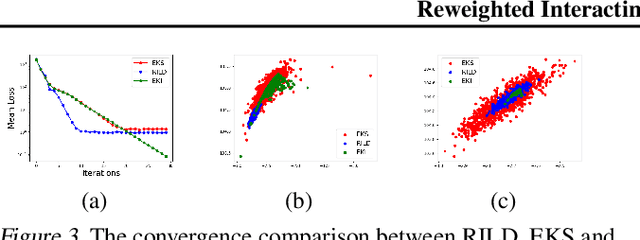
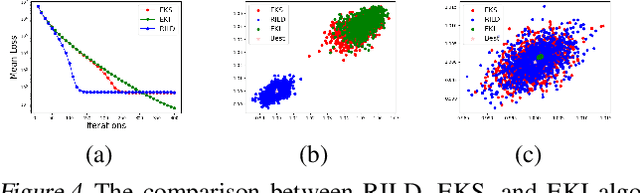
We proposed a new technique to accelerate sampling methods for solving difficult optimization problems. Our method investigates the intrinsic connection between posterior distribution sampling and optimization with Langevin dynamics, and then we propose an interacting particle scheme that approximates a Reweighted Interacting Langevin Diffusion system (RILD). The underlying system is designed by adding a multiplicative source term into the classical Langevin operator, leading to a higher convergence rate and a more concentrated invariant measure. We analyze the convergence rate of our algorithm and the improvement compared to existing results in the asymptotic situation. We also design various tests to verify our theoretical results, showing the advantages of accelerating convergence and breaking through barriers of suspicious local minimums, especially in high-dimensional non-convex settings. Our algorithms and analysis shed some light on combining gradient and genetic algorithms using Partial Differential Equations (PDEs) with provable guarantees.

Neighbor Auto-Grouping Graph Neural Networks for Handover Parameter Configuration in Cellular Network

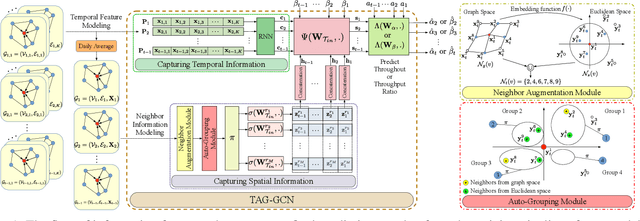
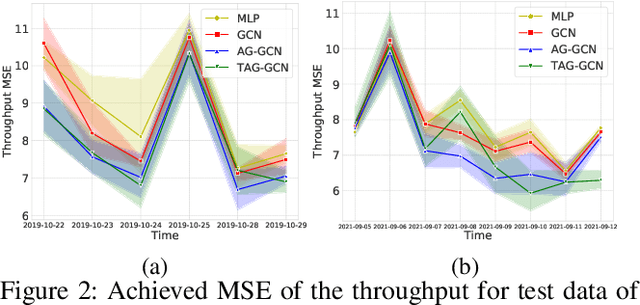
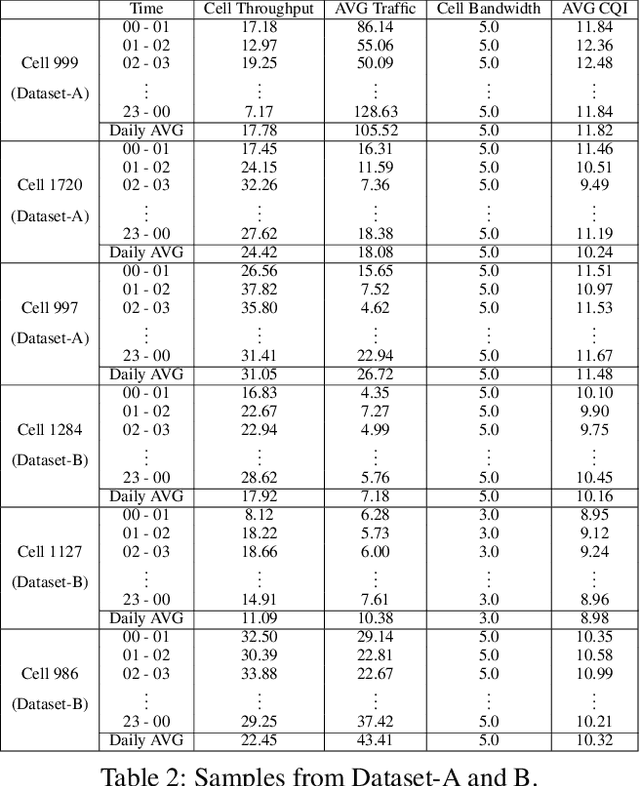
The mobile communication enabled by cellular networks is the one of the main foundations of our modern society. Optimizing the performance of cellular networks and providing massive connectivity with improved coverage and user experience has a considerable social and economic impact on our daily life. This performance relies heavily on the configuration of the network parameters. However, with the massive increase in both the size and complexity of cellular networks, network management, especially parameter configuration, is becoming complicated. The current practice, which relies largely on experts' prior knowledge, is not adequate and will require lots of domain experts and high maintenance costs. In this work, we propose a learning-based framework for handover parameter configuration. The key challenge, in this case, is to tackle the complicated dependencies between neighboring cells and jointly optimize the whole network. Our framework addresses this challenge in two ways. First, we introduce a novel approach to imitate how the network responds to different network states and parameter values, called auto-grouping graph convolutional network (AG-GCN). During the parameter configuration stage, instead of solving the global optimization problem, we design a local multi-objective optimization strategy where each cell considers several local performance metrics to balance its own performance and its neighbors. We evaluate our proposed algorithm via a simulator constructed using real network data. We demonstrate that the handover parameters our model can find, achieve better average network throughput compared to those recommended by experts as well as alternative baselines, which can bring better network quality and stability. It has the potential to massively reduce costs arising from human expert intervention and maintenance.