Kaiyang Guo
Proximalized Preference Optimization for Diverse Feedback Types: A Decomposed Perspective on DPO
May 29, 2025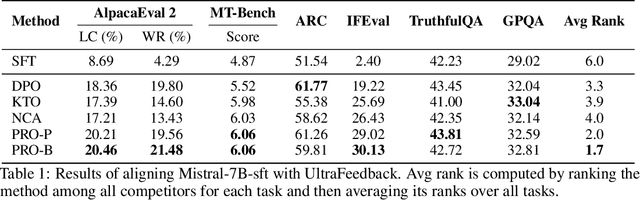


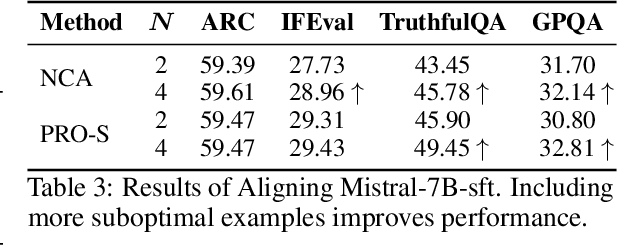
Abstract:Direct alignment methods typically optimize large language models (LLMs) by contrasting the likelihoods of preferred versus dispreferred responses. While effective in steering LLMs to match relative preference, these methods are frequently noted for decreasing the absolute likelihoods of example responses. As a result, aligned models tend to generate outputs that deviate from the expected patterns, exhibiting reward-hacking effect even without a reward model. This undesired consequence exposes a fundamental limitation in contrastive alignment, which we characterize as likelihood underdetermination. In this work, we revisit direct preference optimization (DPO) -- the seminal direct alignment method -- and demonstrate that its loss theoretically admits a decomposed reformulation. The reformulated loss not only broadens applicability to a wider range of feedback types, but also provides novel insights into the underlying cause of likelihood underdetermination. Specifically, the standard DPO implementation implicitly oversimplifies a regularizer in the reformulated loss, and reinstating its complete version effectively resolves the underdetermination issue. Leveraging these findings, we introduce PRoximalized PReference Optimization (PRO), a unified method to align with diverse feeback types, eliminating likelihood underdetermination through an efficient approximation of the complete regularizer. Comprehensive experiments show the superiority of PRO over existing methods in scenarios involving pairwise, binary and scalar feedback.
Generative Models in Decision Making: A Survey
Feb 25, 2025Abstract:In recent years, the exceptional performance of generative models in generative tasks has sparked significant interest in their integration into decision-making processes. Due to their ability to handle complex data distributions and their strong model capacity, generative models can be effectively incorporated into decision-making systems by generating trajectories that guide agents toward high-reward state-action regions or intermediate sub-goals. This paper presents a comprehensive review of the application of generative models in decision-making tasks. We classify seven fundamental types of generative models: energy-based models, generative adversarial networks, variational autoencoders, normalizing flows, diffusion models, generative flow networks, and autoregressive models. Regarding their applications, we categorize their functions into three main roles: controllers, modelers and optimizers, and discuss how each role contributes to decision-making. Furthermore, we examine the deployment of these models across five critical real-world decision-making scenarios. Finally, we summarize the strengths and limitations of current approaches and propose three key directions for advancing next-generation generative directive models: high-performance algorithms, large-scale generalized decision-making models, and self-evolving and adaptive models.
Calibrated One Round Federated Learning with Bayesian Inference in the Predictive Space
Dec 15, 2023
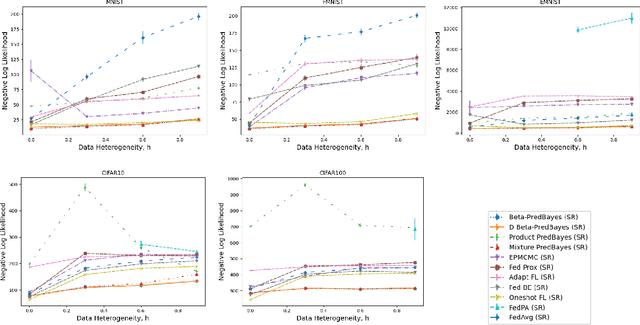
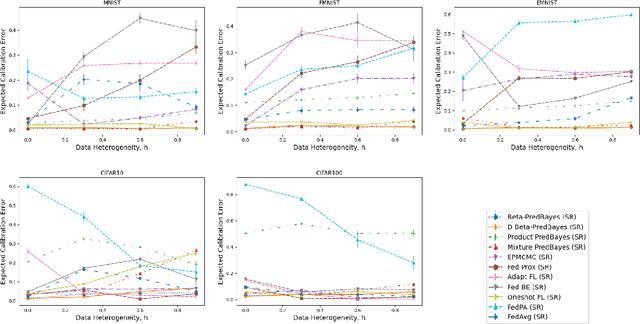
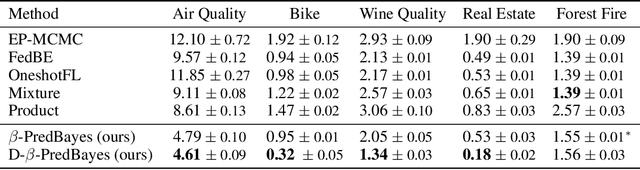
Abstract:Federated Learning (FL) involves training a model over a dataset distributed among clients, with the constraint that each client's dataset is localized and possibly heterogeneous. In FL, small and noisy datasets are common, highlighting the need for well-calibrated models that represent the uncertainty of predictions. The closest FL techniques to achieving such goals are the Bayesian FL methods which collect parameter samples from local posteriors, and aggregate them to approximate the global posterior. To improve scalability for larger models, one common Bayesian approach is to approximate the global predictive posterior by multiplying local predictive posteriors. In this work, we demonstrate that this method gives systematically overconfident predictions, and we remedy this by proposing $\beta$-Predictive Bayes, a Bayesian FL algorithm that interpolates between a mixture and product of the predictive posteriors, using a tunable parameter $\beta$. This parameter is tuned to improve the global ensemble's calibration, before it is distilled to a single model. Our method is evaluated on a variety of regression and classification datasets to demonstrate its superiority in calibration to other baselines, even as data heterogeneity increases. Code available at https://github.com/hasanmohsin/betaPredBayes_FL
Model-Based Offline Reinforcement Learning with Pessimism-Modulated Dynamics Belief
Oct 13, 2022



Abstract:Model-based offline reinforcement learning (RL) aims to find highly rewarding policy, by leveraging a previously collected static dataset and a dynamics model. While learned through reuse of static dataset, the dynamics model's generalization ability hopefully promotes policy learning if properly utilized. To that end, several works propose to quantify the uncertainty of predicted dynamics, and explicitly apply it to penalize reward. However, as the dynamics and the reward are intrinsically different factors in context of MDP, characterizing the impact of dynamics uncertainty through reward penalty may incur unexpected tradeoff between model utilization and risk avoidance. In this work, we instead maintain a belief distribution over dynamics, and evaluate/optimize policy through biased sampling from the belief. The sampling procedure, biased towards pessimism, is derived based on an alternating Markov game formulation of offline RL. We formally show that the biased sampling naturally induces an updated dynamics belief with policy-dependent reweighting factor, termed Pessimism-Modulated Dynamics Belief. To improve policy, we devise an iterative regularized policy optimization algorithm for the game, with guarantee of monotonous improvement under certain condition. To make practical, we further devise an offline RL algorithm to approximately find the solution. Empirical results show that the proposed approach achieves state-of-the-art performance on a wide range of benchmark tasks.
Robust One Round Federated Learning with Predictive Space Bayesian Inference
Jun 20, 2022


Abstract:Making predictions robust is an important challenge. A separate challenge in federated learning (FL) is to reduce the number of communication rounds, particularly since doing so reduces performance in heterogeneous data settings. To tackle both issues, we take a Bayesian perspective on the problem of learning a global model. We show how the global predictive posterior can be approximated using client predictive posteriors. This is unlike other works which aggregate the local model space posteriors into the global model space posterior, and are susceptible to high approximation errors due to the posterior's high dimensional multimodal nature. In contrast, our method performs the aggregation on the predictive posteriors, which are typically easier to approximate owing to the low-dimensionality of the output space. We present an algorithm based on this idea, which performs MCMC sampling at each client to obtain an estimate of the local posterior, and then aggregates these in one round to obtain a global ensemble model. Through empirical evaluation on several classification and regression tasks, we show that despite using one round of communication, the method is competitive with other FL techniques, and outperforms them on heterogeneous settings. The code is publicly available at https://github.com/hasanmohsin/FedPredSpace_1Round.
Personalized Federated Learning via Variational Bayesian Inference
Jun 16, 2022
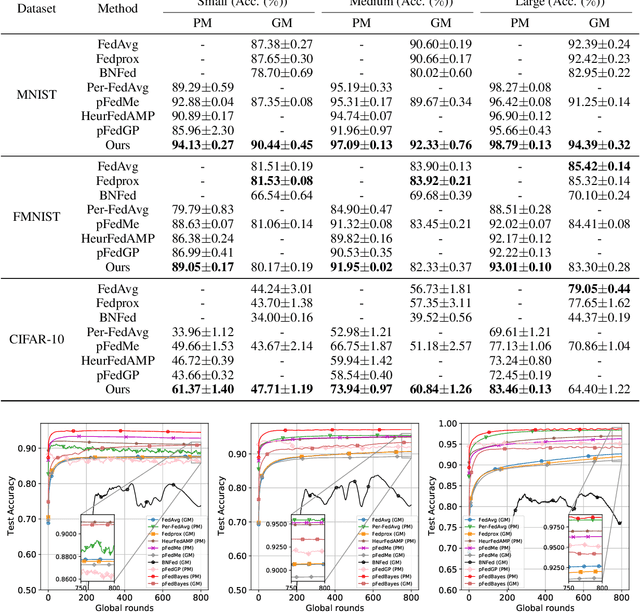


Abstract:Federated learning faces huge challenges from model overfitting due to the lack of data and statistical diversity among clients. To address these challenges, this paper proposes a novel personalized federated learning method via Bayesian variational inference named pFedBayes. To alleviate the overfitting, weight uncertainty is introduced to neural networks for clients and the server. To achieve personalization, each client updates its local distribution parameters by balancing its construction error over private data and its KL divergence with global distribution from the server. Theoretical analysis gives an upper bound of averaged generalization error and illustrates that the convergence rate of the generalization error is minimax optimal up to a logarithmic factor. Experiments show that the proposed method outperforms other advanced personalized methods on personalized models, e.g., pFedBayes respectively outperforms other SOTA algorithms by 1.25%, 0.42% and 11.71% on MNIST, FMNIST and CIFAR-10 under non-i.i.d. limited data.
Federated Bayesian Neural Regression: A Scalable Global Federated Gaussian Process
Jun 13, 2022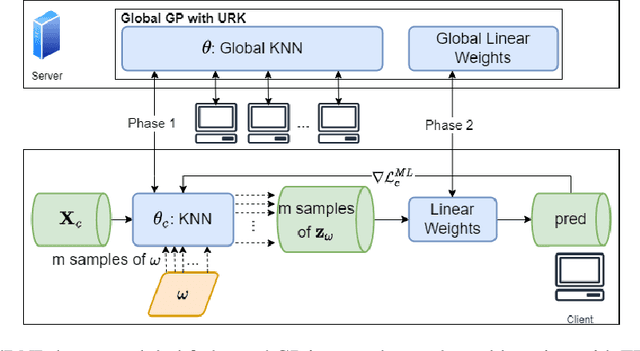
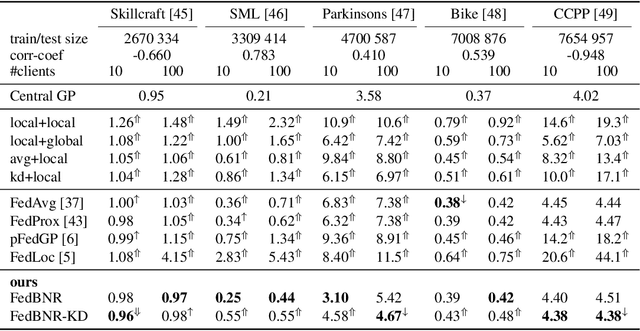
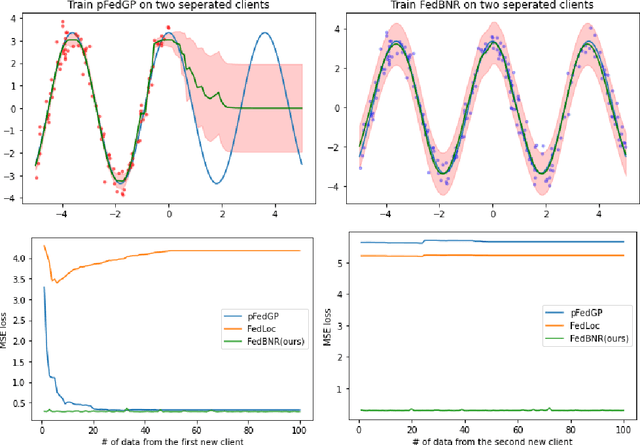
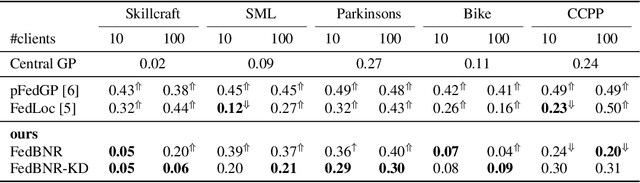
Abstract:In typical scenarios where the Federated Learning (FL) framework applies, it is common for clients to have insufficient training data to produce an accurate model. Thus, models that provide not only point estimations, but also some notion of confidence are beneficial. Gaussian Process (GP) is a powerful Bayesian model that comes with naturally well-calibrated variance estimations. However, it is challenging to learn a stand-alone global GP since merging local kernels leads to privacy leakage. To preserve privacy, previous works that consider federated GPs avoid learning a global model by focusing on the personalized setting or learning an ensemble of local models. We present Federated Bayesian Neural Regression (FedBNR), an algorithm that learns a scalable stand-alone global federated GP that respects clients' privacy. We incorporate deep kernel learning and random features for scalability by defining a unifying random kernel. We show this random kernel can recover any stationary kernel and many non-stationary kernels. We then derive a principled approach of learning a global predictive model as if all client data is centralized. We also learn global kernels with knowledge distillation methods for non-identically and independently distributed (non-i.i.d.) clients. Experiments are conducted on real-world regression datasets and show statistically significant improvements compared to other federated GP models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge