Neighbor Auto-Grouping Graph Neural Networks for Handover Parameter Configuration in Cellular Network

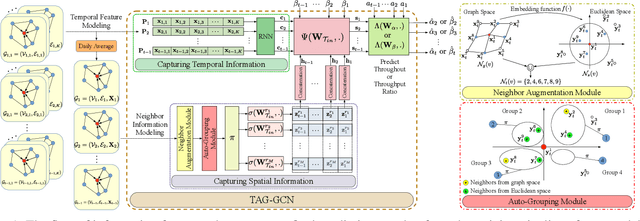
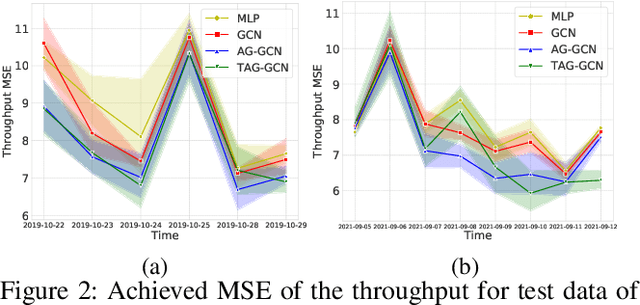
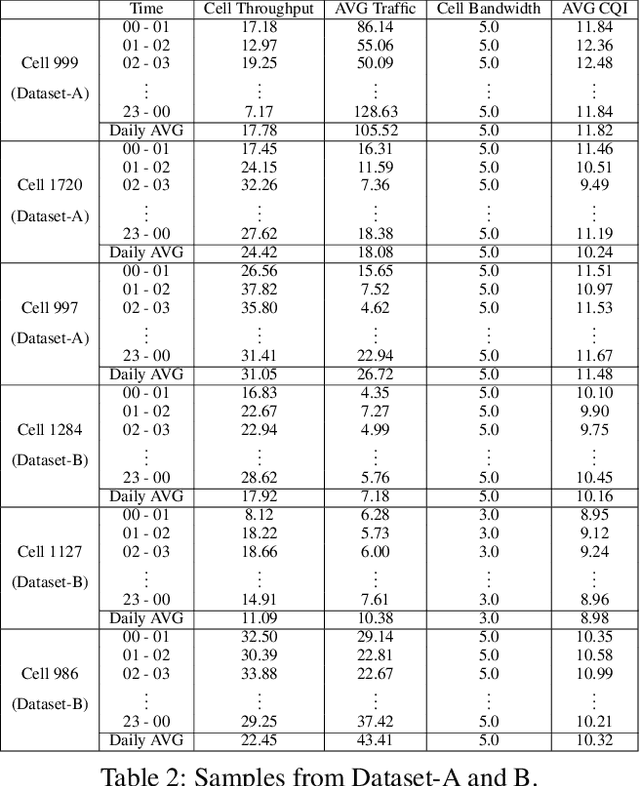
The mobile communication enabled by cellular networks is the one of the main foundations of our modern society. Optimizing the performance of cellular networks and providing massive connectivity with improved coverage and user experience has a considerable social and economic impact on our daily life. This performance relies heavily on the configuration of the network parameters. However, with the massive increase in both the size and complexity of cellular networks, network management, especially parameter configuration, is becoming complicated. The current practice, which relies largely on experts' prior knowledge, is not adequate and will require lots of domain experts and high maintenance costs. In this work, we propose a learning-based framework for handover parameter configuration. The key challenge, in this case, is to tackle the complicated dependencies between neighboring cells and jointly optimize the whole network. Our framework addresses this challenge in two ways. First, we introduce a novel approach to imitate how the network responds to different network states and parameter values, called auto-grouping graph convolutional network (AG-GCN). During the parameter configuration stage, instead of solving the global optimization problem, we design a local multi-objective optimization strategy where each cell considers several local performance metrics to balance its own performance and its neighbors. We evaluate our proposed algorithm via a simulator constructed using real network data. We demonstrate that the handover parameters our model can find, achieve better average network throughput compared to those recommended by experts as well as alternative baselines, which can bring better network quality and stability. It has the potential to massively reduce costs arising from human expert intervention and maintenance.

Model-Based Offline Reinforcement Learning with Pessimism-Modulated Dynamics Belief

Model-based offline reinforcement learning (RL) aims to find highly rewarding policy, by leveraging a previously collected static dataset and a dynamics model. While learned through reuse of static dataset, the dynamics model's generalization ability hopefully promotes policy learning if properly utilized. To that end, several works propose to quantify the uncertainty of predicted dynamics, and explicitly apply it to penalize reward. However, as the dynamics and the reward are intrinsically different factors in context of MDP, characterizing the impact of dynamics uncertainty through reward penalty may incur unexpected tradeoff between model utilization and risk avoidance. In this work, we instead maintain a belief distribution over dynamics, and evaluate/optimize policy through biased sampling from the belief. The sampling procedure, biased towards pessimism, is derived based on an alternating Markov game formulation of offline RL. We formally show that the biased sampling naturally induces an updated dynamics belief with policy-dependent reweighting factor, termed Pessimism-Modulated Dynamics Belief. To improve policy, we devise an iterative regularized policy optimization algorithm for the game, with guarantee of monotonous improvement under certain condition. To make practical, we further devise an offline RL algorithm to approximately find the solution. Empirical results show that the proposed approach achieves state-of-the-art performance on a wide range of benchmark tasks.

Node Copying: A Random Graph Model for Effective Graph Sampling

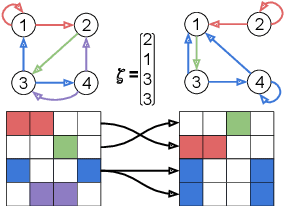
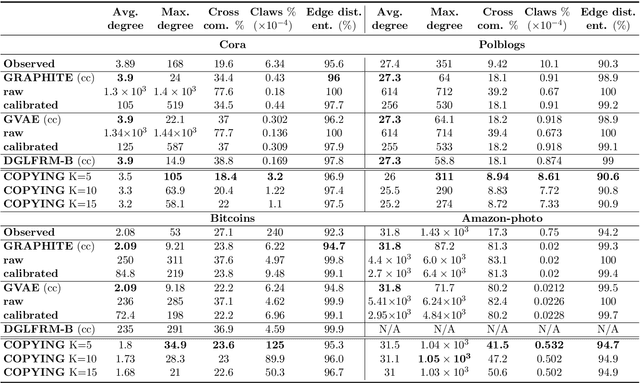
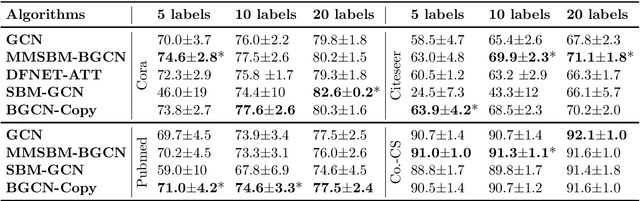
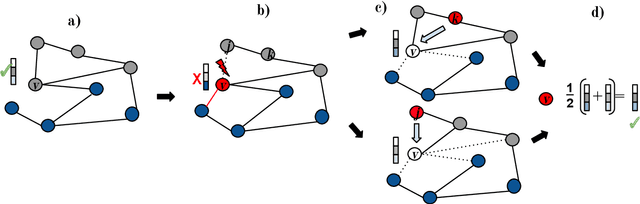
There has been an increased interest in applying machine learning techniques on relational structured-data based on an observed graph. Often, this graph is not fully representative of the true relationship amongst nodes. In these settings, building a generative model conditioned on the observed graph allows to take the graph uncertainty into account. Various existing techniques either rely on restrictive assumptions, fail to preserve topological properties within the samples or are prohibitively expensive for larger graphs. In this work, we introduce the node copying model for constructing a distribution over graphs. Sampling of a random graph is carried out by replacing each node's neighbors by those of a randomly sampled similar node. The sampled graphs preserve key characteristics of the graph structure without explicitly targeting them. Additionally, sampling from this model is extremely simple and scales linearly with the nodes. We show the usefulness of the copying model in three tasks. First, in node classification, a Bayesian formulation based on node copying achieves higher accuracy in sparse data settings. Second, we employ our proposed model to mitigate the effect of adversarial attacks on the graph topology. Last, incorporation of the model in a recommendation system setting improves recall over state-of-the-art methods.

Universality of parametric Coupling Flows over parametric diffeomorphisms

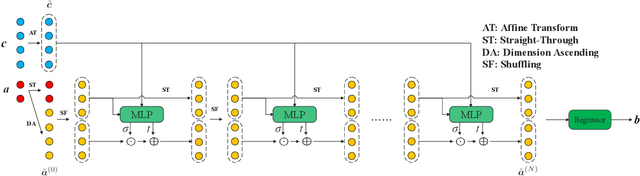
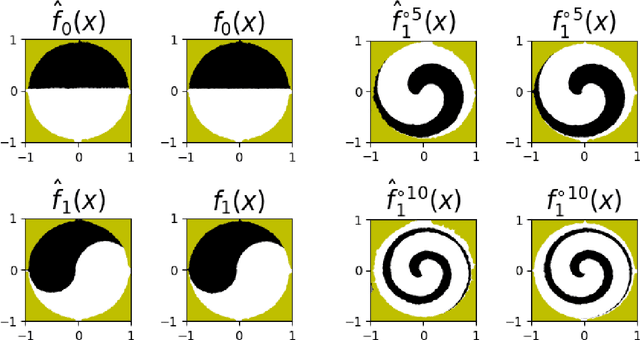
Invertible neural networks based on Coupling Flows CFlows) have various applications such as image synthesis and data compression. The approximation universality for CFlows is of paramount importance to ensure the model expressiveness. In this paper, we prove that CFlows can approximate any diffeomorphism in C^k-norm if its layers can approximate certain single-coordinate transforms. Specifically, we derive that a composition of affine coupling layers and invertible linear transforms achieves this universality. Furthermore, in parametric cases where the diffeomorphism depends on some extra parameters, we prove the corresponding approximation theorems for our proposed parametric coupling flows named Para-CFlows. In practice, we apply Para-CFlows as a neural surrogate model in contextual Bayesian optimization tasks, to demonstrate its superiority over other neural surrogate models in terms of optimization performance.

Clustering Causal Additive Noise Models

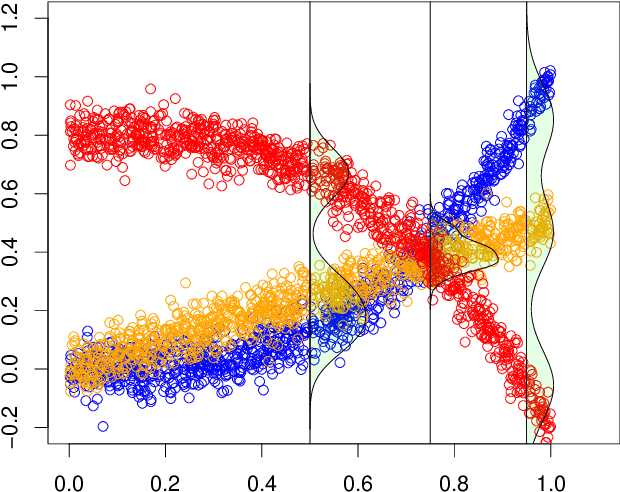
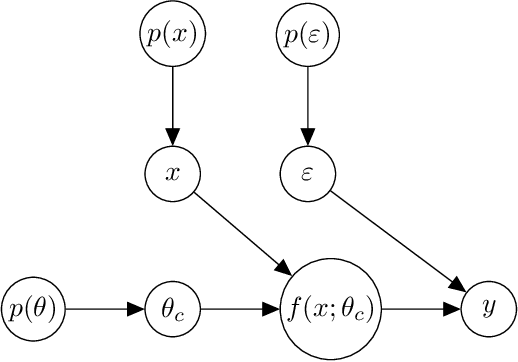
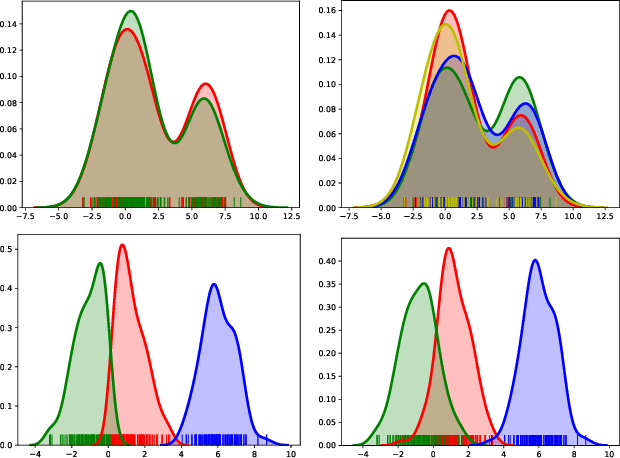
Additive noise models are commonly used to infer the causal direction for a given set of observed data. Most causal models assume a single homogeneous population. However, observations may be collected under different conditions in practice. Such data often require models that can accommodate possible heterogeneity caused by different conditions under which data have been collected. We propose a clustering algorithm inspired by the $k$-means algorithm, but with unknown $k$. Using the proposed algorithm, both the labels and the number of components are estimated from the collected data. The estimated labels are used to adjust the causal direction test statistic. The adjustment significantly improves the performance of the test statistic in identifying the correct causal direction.

Causal Inference and Mechanism Clustering of A Mixture of Additive Noise Models

The inference of the causal relationship between a pair of observed variables is a fundamental problem in science, and most existing approaches are based on one single causal model. In practice, however, observations are often collected from multiple sources with heterogeneous causal models due to certain uncontrollable factors, which renders causal analysis results obtained by a single model skeptical. In this paper, we generalize the Additive Noise Model (ANM) to a mixture model, which consists of a finite number of ANMs, and provide the condition of its causal identifiability. To conduct model estimation, we propose Gaussian Process Partially Observable Model (GPPOM), and incorporate independence enforcement into it to learn latent parameter associated with each observation. Causal inference and clustering according to the underlying generating mechanisms of the mixture model are addressed in this work. Experiments on synthetic and real data demonstrate the effectiveness of our proposed approach.