Universality of parametric Coupling Flows over parametric diffeomorphisms
Paper and Code
Feb 08, 2022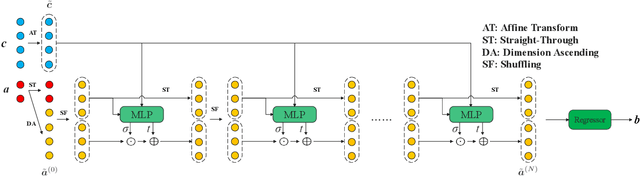

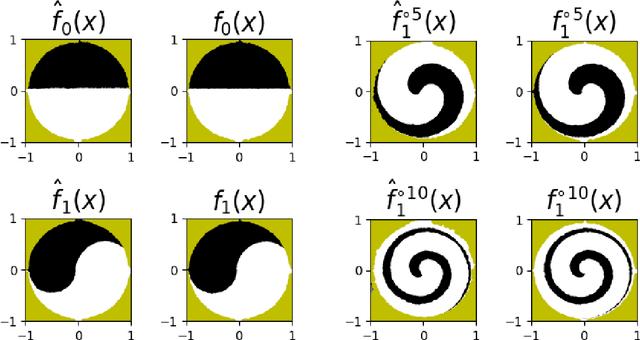

Invertible neural networks based on Coupling Flows CFlows) have various applications such as image synthesis and data compression. The approximation universality for CFlows is of paramount importance to ensure the model expressiveness. In this paper, we prove that CFlows can approximate any diffeomorphism in C^k-norm if its layers can approximate certain single-coordinate transforms. Specifically, we derive that a composition of affine coupling layers and invertible linear transforms achieves this universality. Furthermore, in parametric cases where the diffeomorphism depends on some extra parameters, we prove the corresponding approximation theorems for our proposed parametric coupling flows named Para-CFlows. In practice, we apply Para-CFlows as a neural surrogate model in contextual Bayesian optimization tasks, to demonstrate its superiority over other neural surrogate models in terms of optimization performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge