Efficient Robust Bayesian Optimization for Arbitrary Uncertain Inputs

Bayesian Optimization (BO) is a sample-efficient optimization algorithm widely employed across various applications. In some challenging BO tasks, input uncertainty arises due to the inevitable randomness in the optimization process, such as machining errors, execution noise, or contextual variability. This uncertainty deviates the input from the intended value before evaluation, resulting in significant performance fluctuations in the final result. In this paper, we introduce a novel robust Bayesian Optimization algorithm, AIRBO, which can effectively identify a robust optimum that performs consistently well under arbitrary input uncertainty. Our method directly models the uncertain inputs of arbitrary distributions by empowering the Gaussian Process with the Maximum Mean Discrepancy (MMD) and further accelerates the posterior inference via Nystrom approximation. Rigorous theoretical regret bound is established under MMD estimation error and extensive experiments on synthetic functions and real problems demonstrate that our approach can handle various input uncertainties and achieve state-of-the-art performance.

Convergence guarantee for consistency models

We provide the first convergence guarantees for the Consistency Models (CMs), a newly emerging type of one-step generative models that can generate comparable samples to those generated by Diffusion Models. Our main result is that, under the basic assumptions on score-matching errors, consistency errors and smoothness of the data distribution, CMs can efficiently sample from any realistic data distribution in one step with small $W_2$ error. Our results (1) hold for $L^2$-accurate score and consistency assumption (rather than $L^\infty$-accurate); (2) do note require strong assumptions on the data distribution such as log-Sobelev inequality; (3) scale polynomially in all parameters; and (4) match the state-of-the-art convergence guarantee for score-based generative models (SGMs). We also provide the result that the Multistep Consistency Sampling procedure can further reduce the error comparing to one step sampling, which support the original statement of "Consistency Models, Yang Song 2023". Our result further imply a TV error guarantee when take some Langevin-based modifications to the output distributions.

Reweighted Interacting Langevin Diffusions: an Accelerated Sampling Methodfor Optimization

We proposed a new technique to accelerate sampling methods for solving difficult optimization problems. Our method investigates the intrinsic connection between posterior distribution sampling and optimization with Langevin dynamics, and then we propose an interacting particle scheme that approximates a Reweighted Interacting Langevin Diffusion system (RILD). The underlying system is designed by adding a multiplicative source term into the classical Langevin operator, leading to a higher convergence rate and a more concentrated invariant measure. We analyze the convergence rate of our algorithm and the improvement compared to existing results in the asymptotic situation. We also design various tests to verify our theoretical results, showing the advantages of accelerating convergence and breaking through barriers of suspicious local minimums, especially in high-dimensional non-convex settings. Our algorithms and analysis shed some light on combining gradient and genetic algorithms using Partial Differential Equations (PDEs) with provable guarantees.

Universality of parametric Coupling Flows over parametric diffeomorphisms

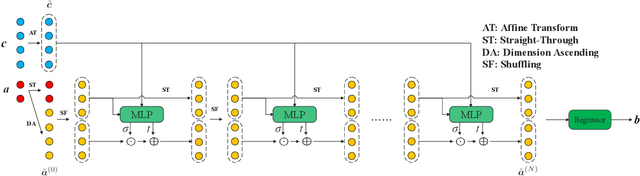
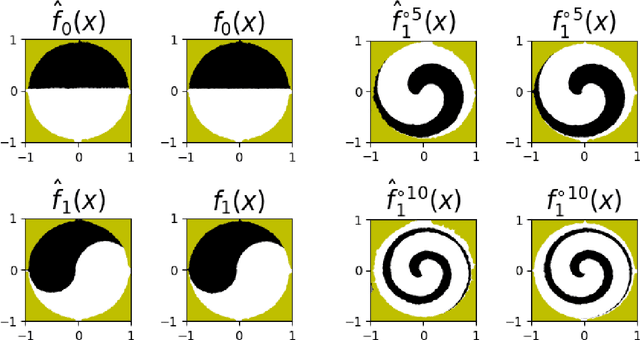
Invertible neural networks based on Coupling Flows CFlows) have various applications such as image synthesis and data compression. The approximation universality for CFlows is of paramount importance to ensure the model expressiveness. In this paper, we prove that CFlows can approximate any diffeomorphism in C^k-norm if its layers can approximate certain single-coordinate transforms. Specifically, we derive that a composition of affine coupling layers and invertible linear transforms achieves this universality. Furthermore, in parametric cases where the diffeomorphism depends on some extra parameters, we prove the corresponding approximation theorems for our proposed parametric coupling flows named Para-CFlows. In practice, we apply Para-CFlows as a neural surrogate model in contextual Bayesian optimization tasks, to demonstrate its superiority over other neural surrogate models in terms of optimization performance.