Reweighted Interacting Langevin Diffusions: an Accelerated Sampling Methodfor Optimization
Paper and Code
Jan 30, 2023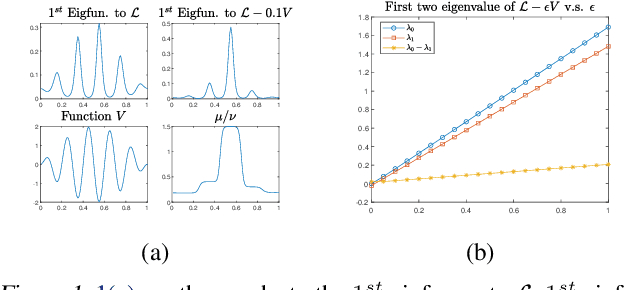
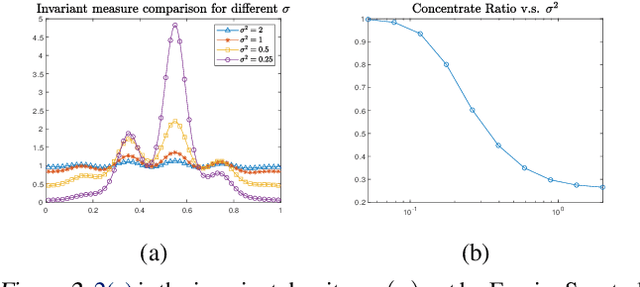
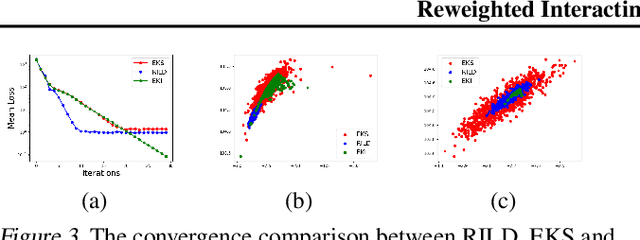
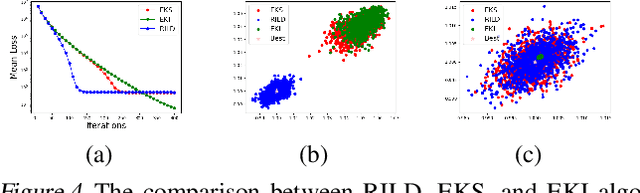
We proposed a new technique to accelerate sampling methods for solving difficult optimization problems. Our method investigates the intrinsic connection between posterior distribution sampling and optimization with Langevin dynamics, and then we propose an interacting particle scheme that approximates a Reweighted Interacting Langevin Diffusion system (RILD). The underlying system is designed by adding a multiplicative source term into the classical Langevin operator, leading to a higher convergence rate and a more concentrated invariant measure. We analyze the convergence rate of our algorithm and the improvement compared to existing results in the asymptotic situation. We also design various tests to verify our theoretical results, showing the advantages of accelerating convergence and breaking through barriers of suspicious local minimums, especially in high-dimensional non-convex settings. Our algorithms and analysis shed some light on combining gradient and genetic algorithms using Partial Differential Equations (PDEs) with provable guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge