Learnable Similarity and Dissimilarity Guided Symmetric Non-Negative Matrix Factorization

Symmetric nonnegative matrix factorization (SymNMF) is a powerful tool for clustering, which typically uses the $k$-nearest neighbor ($k$-NN) method to construct similarity matrix. However, $k$-NN may mislead clustering since the neighbors may belong to different clusters, and its reliability generally decreases as $k$ grows. In this paper, we construct the similarity matrix as a weighted $k$-NN graph with learnable weight that reflects the reliability of each $k$-th NN. This approach reduces the search space of the similarity matrix learning to $n - 1$ dimension, as opposed to the $\mathcal{O}(n^2)$ dimension of existing methods, where $n$ represents the number of samples. Moreover, to obtain a discriminative similarity matrix, we introduce a dissimilarity matrix with a dual structure of the similarity matrix, and propose a new form of orthogonality regularization with discussions on its geometric interpretation and numerical stability. An efficient alternative optimization algorithm is designed to solve the proposed model, with theoretically guarantee that the variables converge to a stationary point that satisfies the KKT conditions. The advantage of the proposed model is demonstrated by the comparison with nine state-of-the-art clustering methods on eight datasets. The code is available at \url{https://github.com/lwl-learning/LSDGSymNMF}.

Efficient Robust Bayesian Optimization for Arbitrary Uncertain Inputs

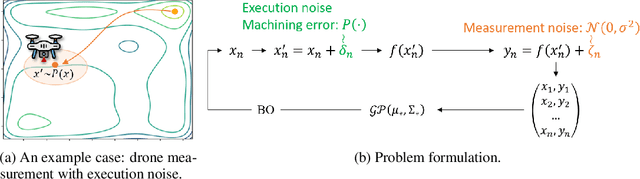
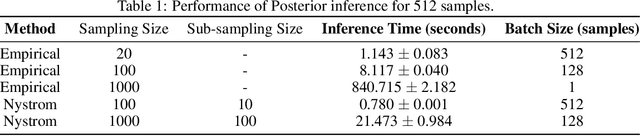
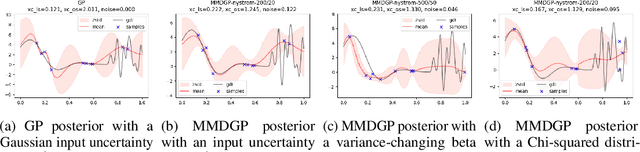
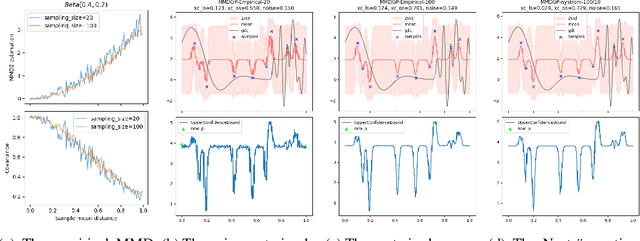
Bayesian Optimization (BO) is a sample-efficient optimization algorithm widely employed across various applications. In some challenging BO tasks, input uncertainty arises due to the inevitable randomness in the optimization process, such as machining errors, execution noise, or contextual variability. This uncertainty deviates the input from the intended value before evaluation, resulting in significant performance fluctuations in the final result. In this paper, we introduce a novel robust Bayesian Optimization algorithm, AIRBO, which can effectively identify a robust optimum that performs consistently well under arbitrary input uncertainty. Our method directly models the uncertain inputs of arbitrary distributions by empowering the Gaussian Process with the Maximum Mean Discrepancy (MMD) and further accelerates the posterior inference via Nystrom approximation. Rigorous theoretical regret bound is established under MMD estimation error and extensive experiments on synthetic functions and real problems demonstrate that our approach can handle various input uncertainties and achieve state-of-the-art performance.

Efficient Bayesian Optimization with Deep Kernel Learning and Transformer Pre-trained on Multiple Heterogeneous Datasets

Bayesian optimization (BO) is widely adopted in black-box optimization problems and it relies on a surrogate model to approximate the black-box response function. With the increasing number of black-box optimization tasks solved and even more to solve, the ability to learn from multiple prior tasks to jointly pre-train a surrogate model is long-awaited to further boost optimization efficiency. In this paper, we propose a simple approach to pre-train a surrogate, which is a Gaussian process (GP) with a kernel defined on deep features learned from a Transformer-based encoder, using datasets from prior tasks with possibly heterogeneous input spaces. In addition, we provide a simple yet effective mix-up initialization strategy for input tokens corresponding to unseen input variables and therefore accelerate new tasks' convergence. Experiments on both synthetic and real benchmark problems demonstrate the effectiveness of our proposed pre-training and transfer BO strategy over existing methods.

Exploring Effective Mask Sampling Modeling for Neural Image Compression

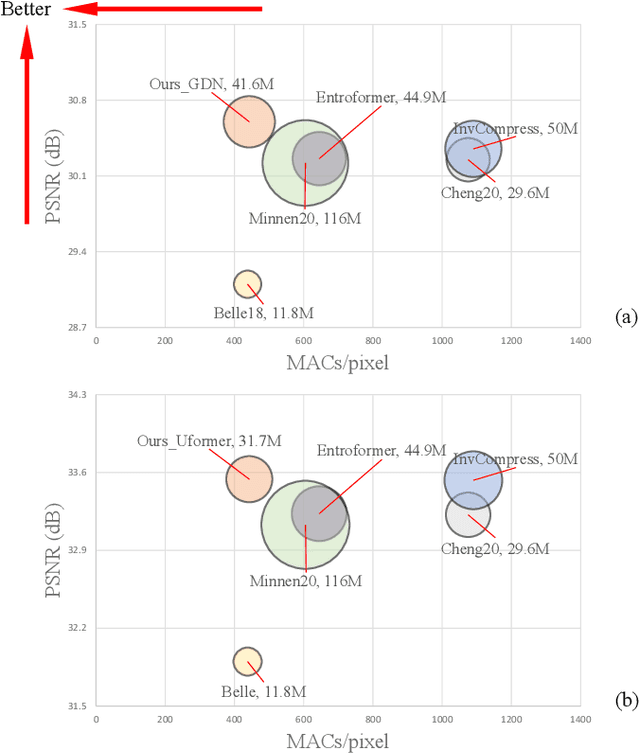
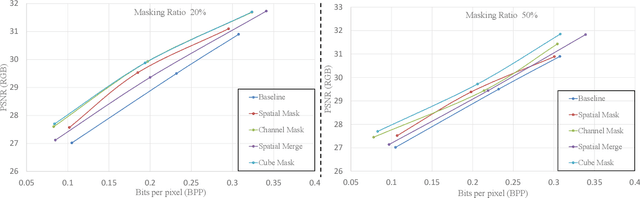
Image compression aims to reduce the information redundancy in images. Most existing neural image compression methods rely on side information from hyperprior or context models to eliminate spatial redundancy, but rarely address the channel redundancy. Inspired by the mask sampling modeling in recent self-supervised learning methods for natural language processing and high-level vision, we propose a novel pretraining strategy for neural image compression. Specifically, Cube Mask Sampling Module (CMSM) is proposed to apply both spatial and channel mask sampling modeling to image compression in the pre-training stage. Moreover, to further reduce channel redundancy, we propose the Learnable Channel Mask Module (LCMM) and the Learnable Channel Completion Module (LCCM). Our plug-and-play CMSM, LCMM, LCCM modules can apply to both CNN-based and Transformer-based architectures, significantly reduce the computational cost, and improve the quality of images. Experiments on the public Kodak and Tecnick datasets demonstrate that our method achieves competitive performance with lower computational complexity compared to state-of-the-art image compression methods.

Reweighted Interacting Langevin Diffusions: an Accelerated Sampling Methodfor Optimization

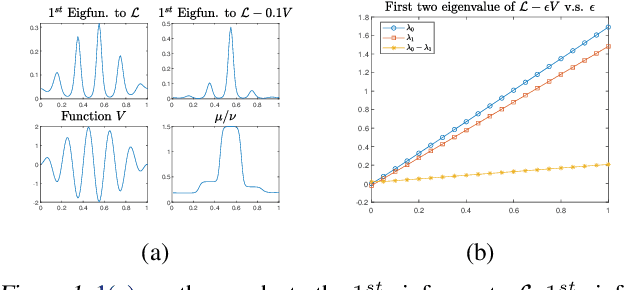
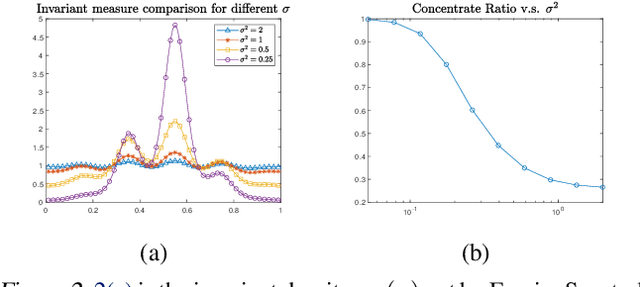
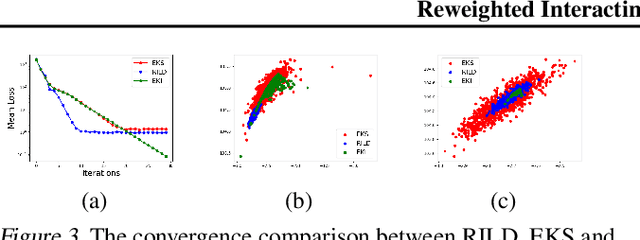
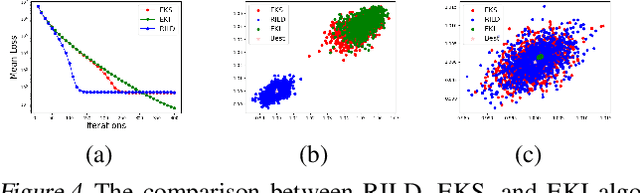
We proposed a new technique to accelerate sampling methods for solving difficult optimization problems. Our method investigates the intrinsic connection between posterior distribution sampling and optimization with Langevin dynamics, and then we propose an interacting particle scheme that approximates a Reweighted Interacting Langevin Diffusion system (RILD). The underlying system is designed by adding a multiplicative source term into the classical Langevin operator, leading to a higher convergence rate and a more concentrated invariant measure. We analyze the convergence rate of our algorithm and the improvement compared to existing results in the asymptotic situation. We also design various tests to verify our theoretical results, showing the advantages of accelerating convergence and breaking through barriers of suspicious local minimums, especially in high-dimensional non-convex settings. Our algorithms and analysis shed some light on combining gradient and genetic algorithms using Partial Differential Equations (PDEs) with provable guarantees.

High-Dimensional Bayesian Optimisation with Variational Autoencoders and Deep Metric Learning

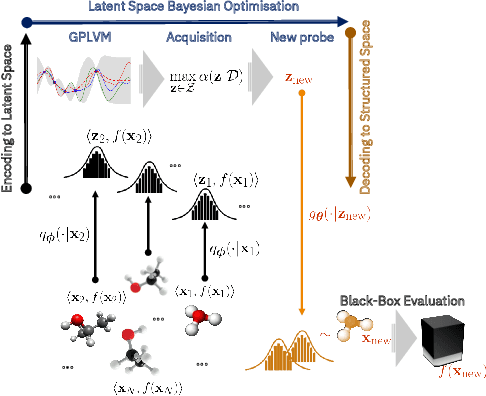
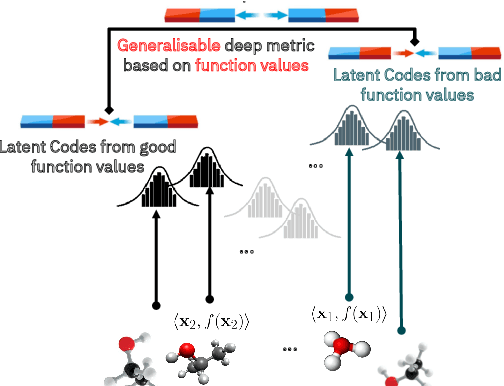
We introduce a method based on deep metric learning to perform Bayesian optimisation over high-dimensional, structured input spaces using variational autoencoders (VAEs). By extending ideas from supervised deep metric learning, we address a longstanding problem in high-dimensional VAE Bayesian optimisation, namely how to enforce a discriminative latent space as an inductive bias. Importantly, we achieve such an inductive bias using just 1% of the available labelled data relative to previous work, highlighting the sample efficiency of our approach. As a theoretical contribution, we present a proof of vanishing regret for our method. As an empirical contribution, we present state-of-the-art results on real-world high-dimensional black-box optimisation problems including property-guided molecule generation. It is the hope that the results presented in this paper can act as a guiding principle for realising effective high-dimensional Bayesian optimisation.

HEBO: Heteroscedastic Evolutionary Bayesian Optimisation

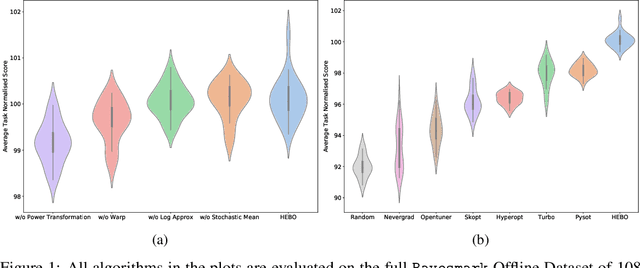
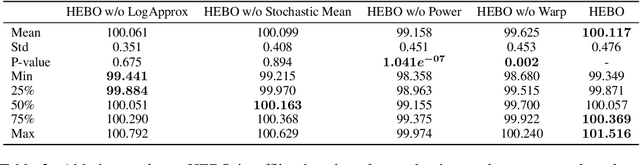
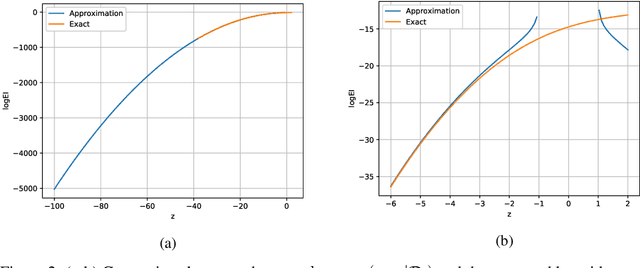
We introduce HEBO: Heteroscedastic Evolutionary Bayesian Optimisation that won the NeurIPS 2020 black-box optimisation competition. We present non-conventional modifications to the surrogate model and acquisition maximisation process and show such a combination superior against all baselines provided by the \texttt{Bayesmark} package. Lastly, we perform an ablation study to highlight the components that contributed to the success of HEBO.

Bayesian Optimization Approach for Analog Circuit Synthesis Using Neural Network

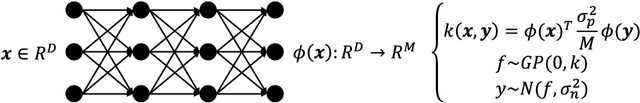
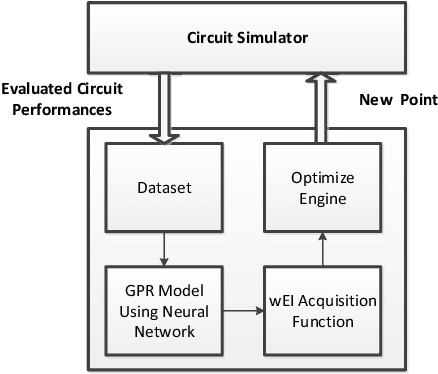
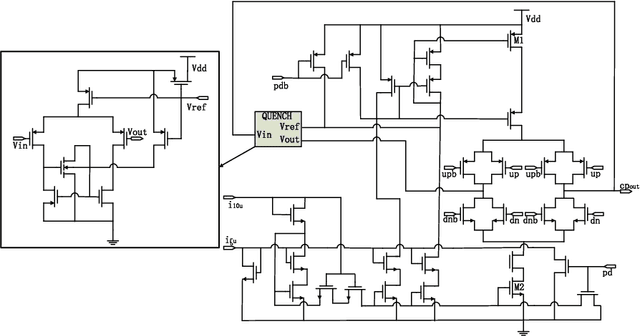
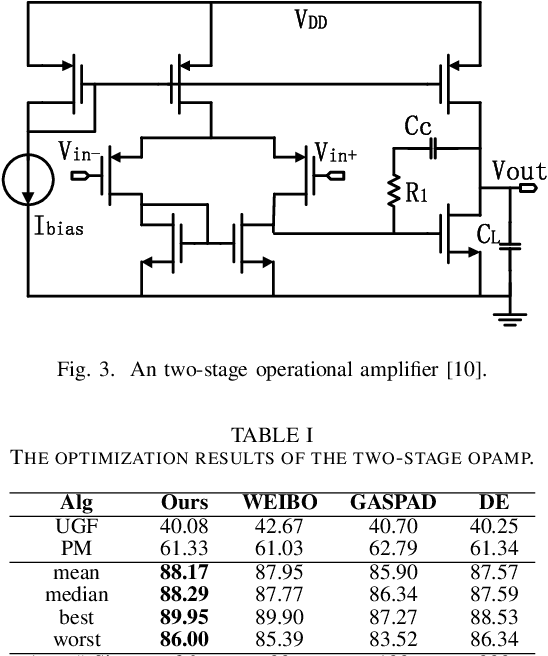
Bayesian optimization with Gaussian process as surrogate model has been successfully applied to analog circuit synthesis. In the traditional Gaussian process regression model, the kernel functions are defined explicitly. The computational complexity of training is O(N 3 ), and the computation complexity of prediction is O(N 2 ), where N is the number of training data. Gaussian process model can also be derived from a weight space view, where the original data are mapped to feature space, and the kernel function is defined as the inner product of nonlinear features. In this paper, we propose a Bayesian optimization approach for analog circuit synthesis using neural network. We use deep neural network to extract good feature representations, and then define Gaussian process using the extracted features. Model averaging method is applied to improve the quality of uncertainty prediction. Compared to Gaussian process model with explicitly defined kernel functions, the neural-network-based Gaussian process model can automatically learn a kernel function from data, which makes it possible to provide more accurate predictions and thus accelerate the follow-up optimization procedure. Also, the neural-network-based model has O(N) training time and constant prediction time. The efficiency of the proposed method has been verified by two real-world analog circuits.