LinEasyBO: Scalable Bayesian Optimization Approach for Analog Circuit Synthesis via One-Dimensional Subspaces

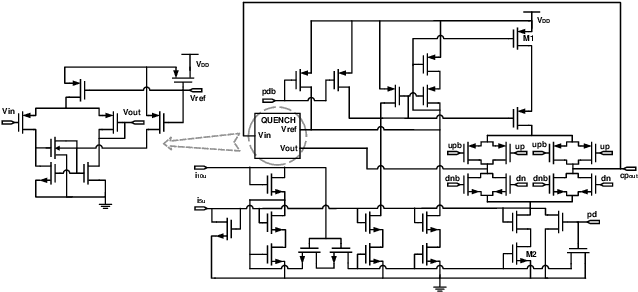
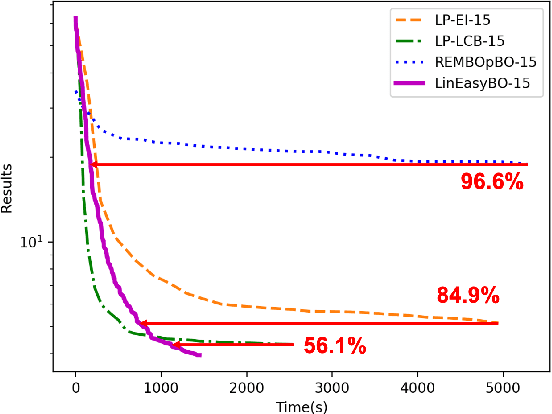
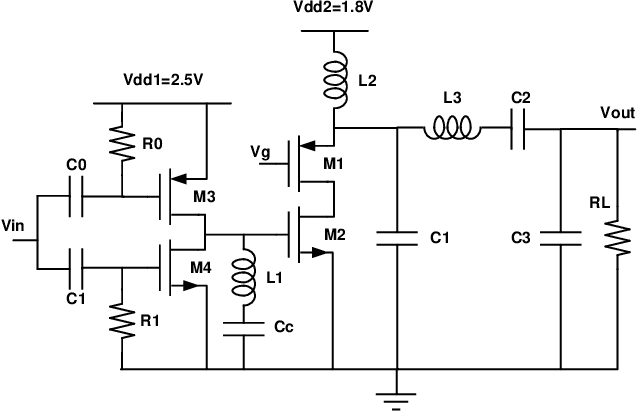
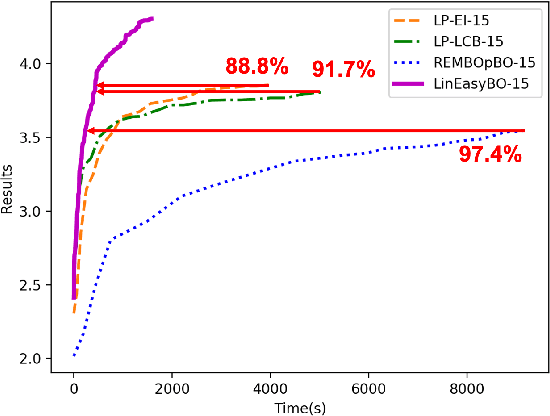
A large body of literature has proved that the Bayesian optimization framework is especially efficient and effective in analog circuit synthesis. However, most of the previous research works only focus on designing informative surrogate models or efficient acquisition functions. Even if searching for the global optimum over the acquisition function surface is itself a difficult task, it has been largely ignored. In this paper, we propose a fast and robust Bayesian optimization approach via one-dimensional subspaces for analog circuit synthesis. By solely focusing on optimizing one-dimension subspaces at each iteration, we greatly reduce the computational overhead of the Bayesian optimization framework while safely maximizing the acquisition function. By combining the benefits of different dimension selection strategies, we adaptively balancing between searching globally and locally. By leveraging the batch Bayesian optimization framework, we further accelerate the optimization procedure by making full use of the hardware resources. Experimental results quantitatively show that our proposed algorithm can accelerate the optimization procedure by up to 9x and 38x compared to LP-EI and REMBOpBO respectively when the batch size is 15.

An Efficient Batch Constrained Bayesian Optimization Approach for Analog Circuit Synthesis via Multi-objective Acquisition Ensemble

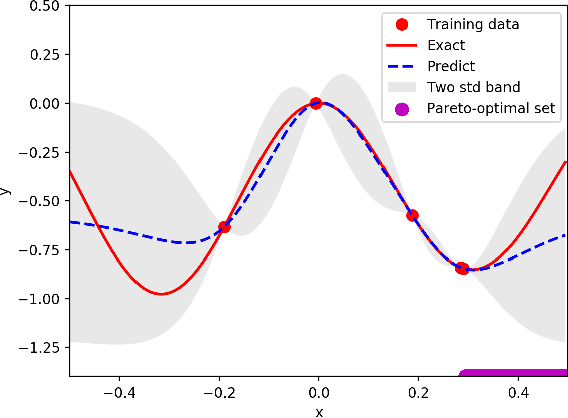
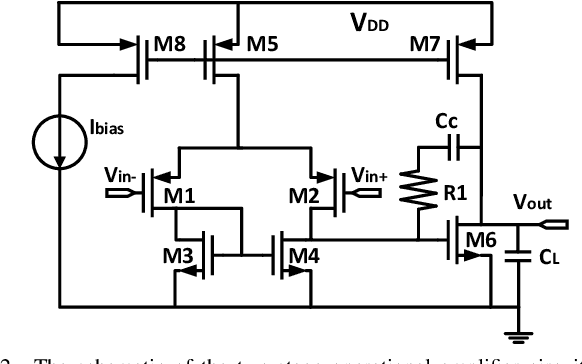
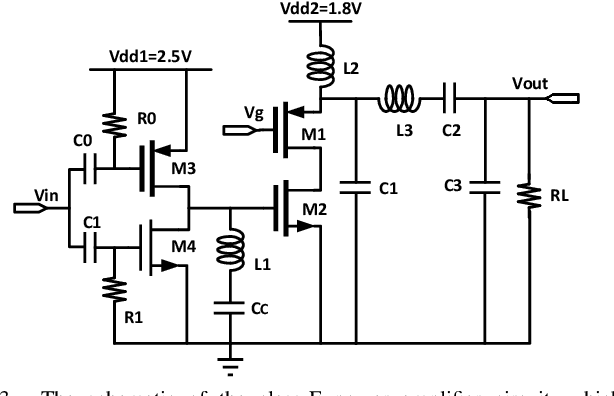
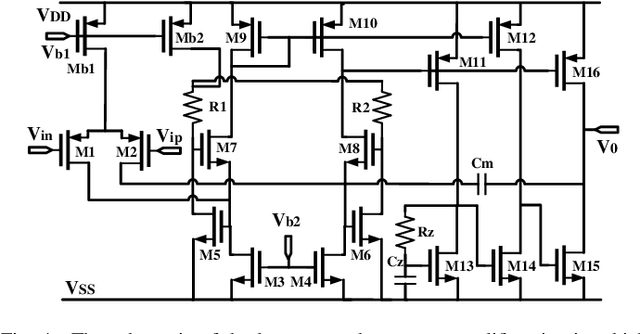
Bayesian optimization is a promising methodology for analog circuit synthesis. However, the sequential nature of the Bayesian optimization framework significantly limits its ability to fully utilize real-world computational resources. In this paper, we propose an efficient parallelizable Bayesian optimization algorithm via Multi-objective ACquisition function Ensemble (MACE) to further accelerate the optimization procedure. By sampling query points from the Pareto front of the probability of improvement (PI), expected improvement (EI) and lower confidence bound (LCB), we combine the benefits of state-of-the-art acquisition functions to achieve a delicate tradeoff between exploration and exploitation for the unconstrained optimization problem. Based on this batch design, we further adjust the algorithm for the constrained optimization problem. By dividing the optimization procedure into two stages and first focusing on finding an initial feasible point, we manage to gain more information about the valid region and can better avoid sampling around the infeasible area. After achieving the first feasible point, we favor the feasible region by adopting a specially designed penalization term to the acquisition function ensemble. The experimental results quantitatively demonstrate that our proposed algorithm can reduce the overall simulation time by up to 74 times compared to differential evolution (DE) for the unconstrained optimization problem when the batch size is 15. For the constrained optimization problem, our proposed algorithm can speed up the optimization process by up to 15 times compared to the weighted expected improvement based Bayesian optimization (WEIBO) approach, when the batch size is 15.

Deep learning of nanopore sensing signals using a bi-path network

Temporary changes in electrical resistance of a nanopore sensor caused by translocating target analytes are recorded as a sequence of pulses on current traces. Prevalent algorithms for feature extraction in pulse-like signals lack objectivity because empirical amplitude thresholds are user-defined to single out the pulses from the noisy background. Here, we use deep learning for feature extraction based on a bi-path network (B-Net). After training, the B-Net acquires the prototypical pulses and the ability of both pulse recognition and feature extraction without a priori assigned parameters. The B-Net performance is evaluated on generated datasets and further applied to experimental data of DNA and protein translocation. The B-Net results show remarkably small relative errors and stable trends. The B-Net is further shown capable of processing data with a signal-to-noise ratio equal to one, an impossibility for threshold-based algorithms. The developed B-Net is generic for pulse-like signals beyond pulsed nanopore currents.

Projection based Active Gaussian Process Regression for Pareto Front Modeling

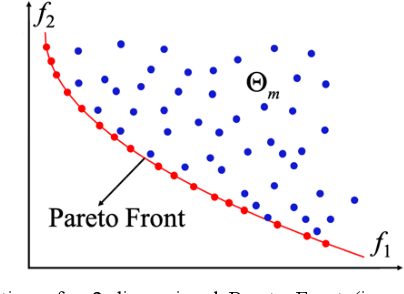
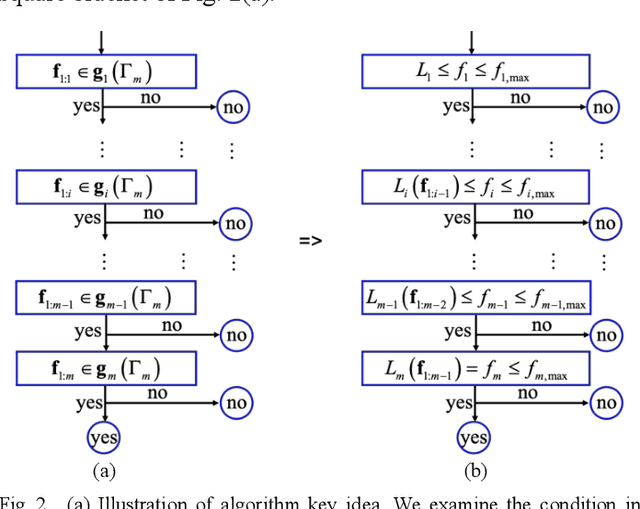
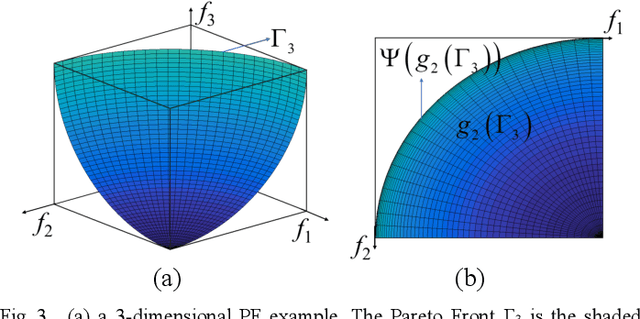
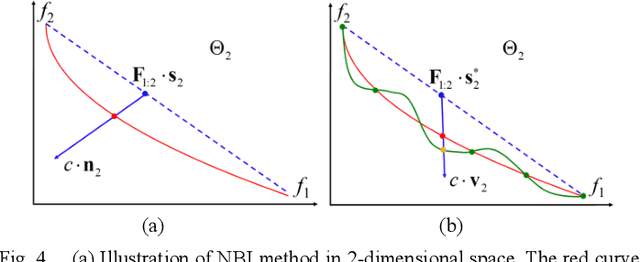
Pareto Front (PF) modeling is essential in decision making problems across all domains such as economics, medicine or engineering. In Operation Research literature, this task has been addressed based on multi-objective optimization algorithms. However, without learning models for PF, these methods cannot examine whether a new provided point locates on PF or not. In this paper, we reconsider the task from Data Mining perspective. A novel projection based active Gaussian process regression (P- aGPR) method is proposed for efficient PF modeling. First, P- aGPR chooses a series of projection spaces with dimensionalities ranking from low to high. Next, in each projection space, a Gaussian process regression (GPR) model is trained to represent the constraint that PF should satisfy in that space. Moreover, in order to improve modeling efficacy and stability, an active learning framework has been developed by exploiting the uncertainty information obtained in the GPR models. Different from all existing methods, our proposed P-aGPR method can not only provide a generative PF model, but also fast examine whether a provided point locates on PF or not. The numerical results demonstrate that compared to state-of-the-art passive learning methods the proposed P-aGPR method can achieve higher modeling accuracy and stability.

Bayesian Optimization Approach for Analog Circuit Synthesis Using Neural Network

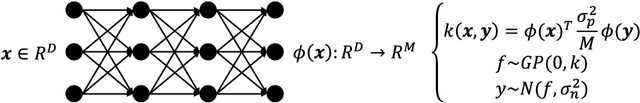
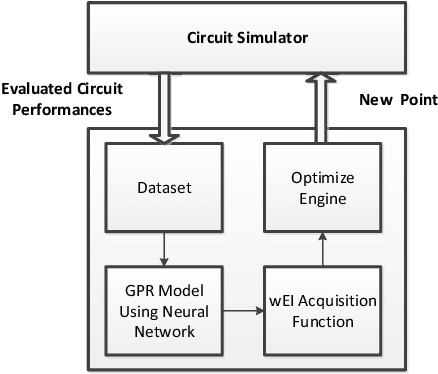
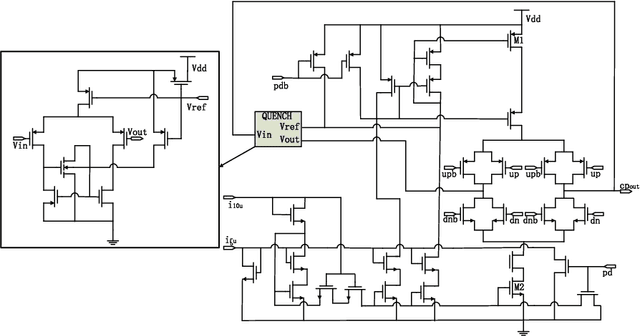
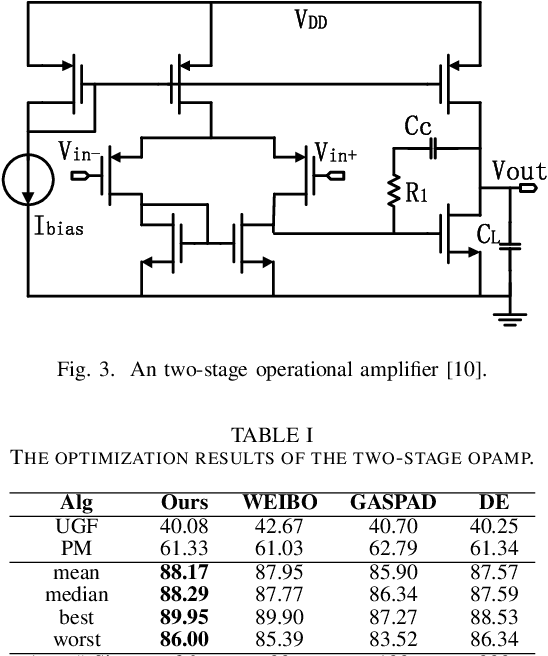
Bayesian optimization with Gaussian process as surrogate model has been successfully applied to analog circuit synthesis. In the traditional Gaussian process regression model, the kernel functions are defined explicitly. The computational complexity of training is O(N 3 ), and the computation complexity of prediction is O(N 2 ), where N is the number of training data. Gaussian process model can also be derived from a weight space view, where the original data are mapped to feature space, and the kernel function is defined as the inner product of nonlinear features. In this paper, we propose a Bayesian optimization approach for analog circuit synthesis using neural network. We use deep neural network to extract good feature representations, and then define Gaussian process using the extracted features. Model averaging method is applied to improve the quality of uncertainty prediction. Compared to Gaussian process model with explicitly defined kernel functions, the neural-network-based Gaussian process model can automatically learn a kernel function from data, which makes it possible to provide more accurate predictions and thus accelerate the follow-up optimization procedure. Also, the neural-network-based model has O(N) training time and constant prediction time. The efficiency of the proposed method has been verified by two real-world analog circuits.