An Efficient Batch Constrained Bayesian Optimization Approach for Analog Circuit Synthesis via Multi-objective Acquisition Ensemble
Paper and Code
Jun 28, 2021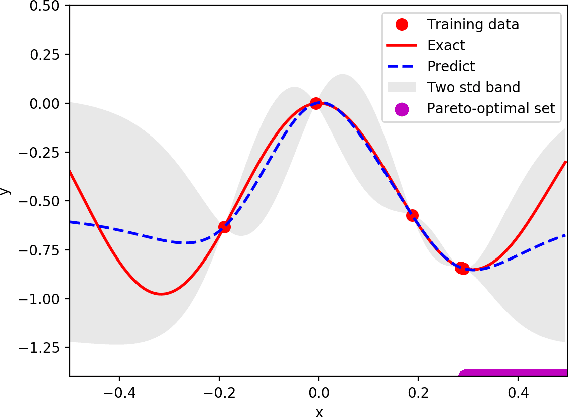
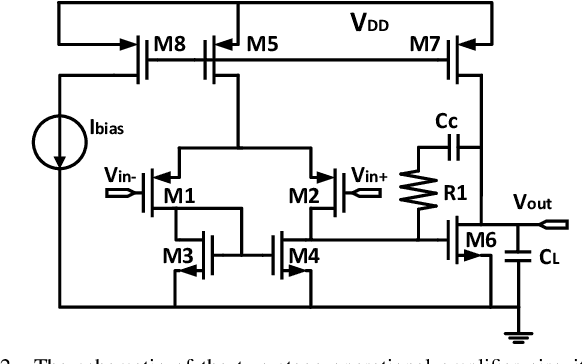
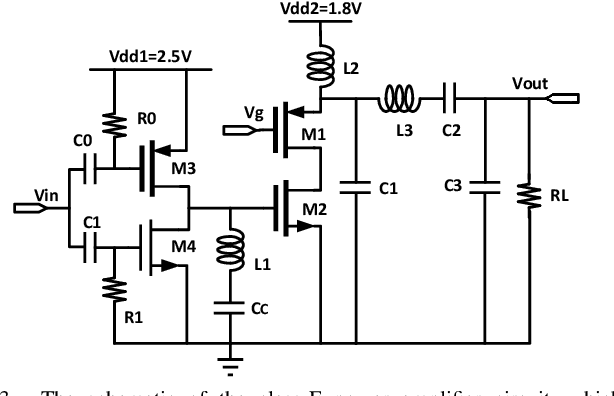
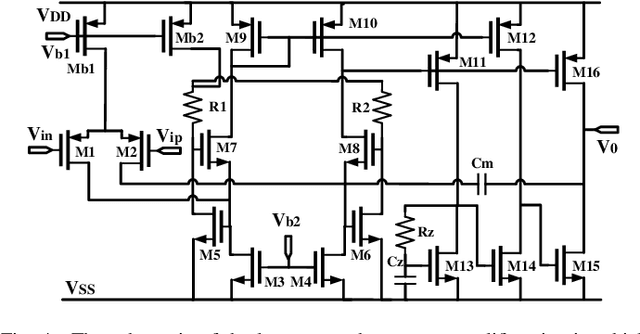
Bayesian optimization is a promising methodology for analog circuit synthesis. However, the sequential nature of the Bayesian optimization framework significantly limits its ability to fully utilize real-world computational resources. In this paper, we propose an efficient parallelizable Bayesian optimization algorithm via Multi-objective ACquisition function Ensemble (MACE) to further accelerate the optimization procedure. By sampling query points from the Pareto front of the probability of improvement (PI), expected improvement (EI) and lower confidence bound (LCB), we combine the benefits of state-of-the-art acquisition functions to achieve a delicate tradeoff between exploration and exploitation for the unconstrained optimization problem. Based on this batch design, we further adjust the algorithm for the constrained optimization problem. By dividing the optimization procedure into two stages and first focusing on finding an initial feasible point, we manage to gain more information about the valid region and can better avoid sampling around the infeasible area. After achieving the first feasible point, we favor the feasible region by adopting a specially designed penalization term to the acquisition function ensemble. The experimental results quantitatively demonstrate that our proposed algorithm can reduce the overall simulation time by up to 74 times compared to differential evolution (DE) for the unconstrained optimization problem when the batch size is 15. For the constrained optimization problem, our proposed algorithm can speed up the optimization process by up to 15 times compared to the weighted expected improvement based Bayesian optimization (WEIBO) approach, when the batch size is 15.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge