Bayesian Optimization Approach for Analog Circuit Synthesis Using Neural Network
Paper and Code
Dec 01, 2019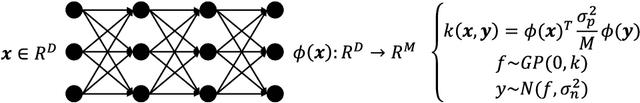
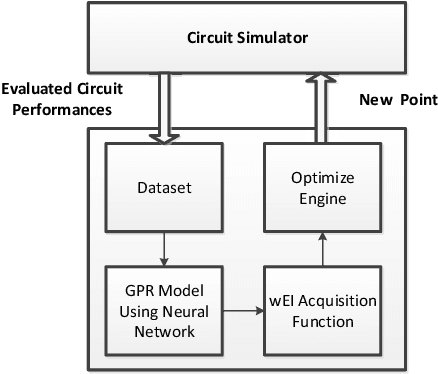
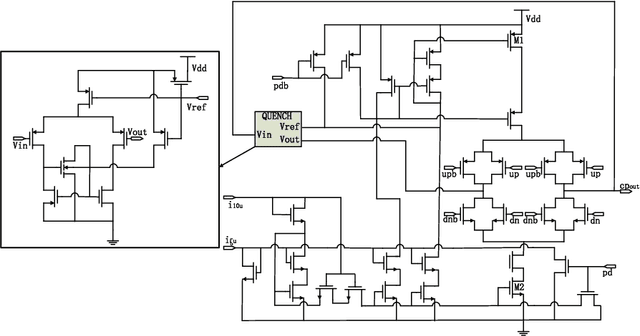
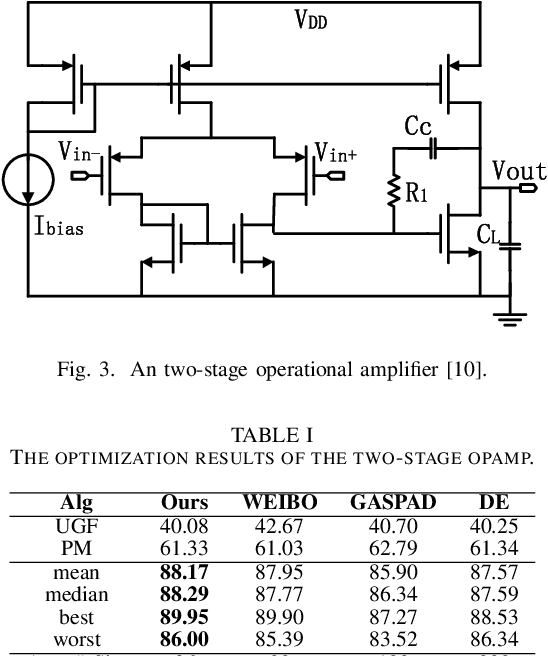
Bayesian optimization with Gaussian process as surrogate model has been successfully applied to analog circuit synthesis. In the traditional Gaussian process regression model, the kernel functions are defined explicitly. The computational complexity of training is O(N 3 ), and the computation complexity of prediction is O(N 2 ), where N is the number of training data. Gaussian process model can also be derived from a weight space view, where the original data are mapped to feature space, and the kernel function is defined as the inner product of nonlinear features. In this paper, we propose a Bayesian optimization approach for analog circuit synthesis using neural network. We use deep neural network to extract good feature representations, and then define Gaussian process using the extracted features. Model averaging method is applied to improve the quality of uncertainty prediction. Compared to Gaussian process model with explicitly defined kernel functions, the neural-network-based Gaussian process model can automatically learn a kernel function from data, which makes it possible to provide more accurate predictions and thus accelerate the follow-up optimization procedure. Also, the neural-network-based model has O(N) training time and constant prediction time. The efficiency of the proposed method has been verified by two real-world analog circuits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge