Efficient Bayesian Optimization with Deep Kernel Learning and Transformer Pre-trained on Multiple Heterogeneous Datasets

Bayesian optimization (BO) is widely adopted in black-box optimization problems and it relies on a surrogate model to approximate the black-box response function. With the increasing number of black-box optimization tasks solved and even more to solve, the ability to learn from multiple prior tasks to jointly pre-train a surrogate model is long-awaited to further boost optimization efficiency. In this paper, we propose a simple approach to pre-train a surrogate, which is a Gaussian process (GP) with a kernel defined on deep features learned from a Transformer-based encoder, using datasets from prior tasks with possibly heterogeneous input spaces. In addition, we provide a simple yet effective mix-up initialization strategy for input tokens corresponding to unseen input variables and therefore accelerate new tasks' convergence. Experiments on both synthetic and real benchmark problems demonstrate the effectiveness of our proposed pre-training and transfer BO strategy over existing methods.

Reframed GES with a Neural Conditional Dependence Measure

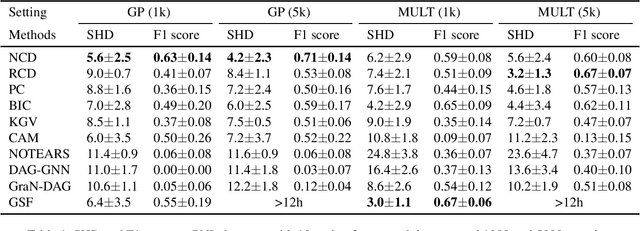
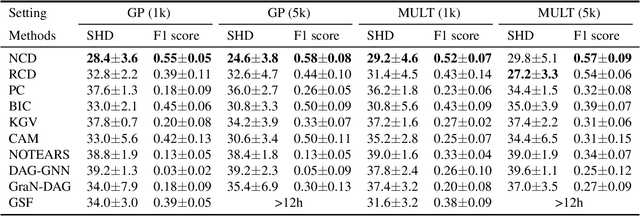
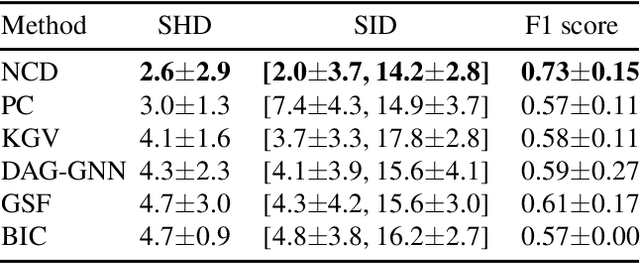
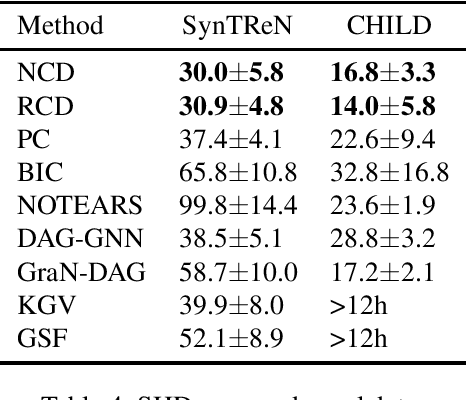
In a nonparametric setting, the causal structure is often identifiable only up to Markov equivalence, and for the purpose of causal inference, it is useful to learn a graphical representation of the Markov equivalence class (MEC). In this paper, we revisit the Greedy Equivalence Search (GES) algorithm, which is widely cited as a score-based algorithm for learning the MEC of the underlying causal structure. We observe that in order to make the GES algorithm consistent in a nonparametric setting, it is not necessary to design a scoring metric that evaluates graphs. Instead, it suffices to plug in a consistent estimator of a measure of conditional dependence to guide the search. We therefore present a reframing of the GES algorithm, which is more flexible than the standard score-based version and readily lends itself to the nonparametric setting with a general measure of conditional dependence. In addition, we propose a neural conditional dependence (NCD) measure, which utilizes the expressive power of deep neural networks to characterize conditional independence in a nonparametric manner. We establish the optimality of the reframed GES algorithm under standard assumptions and the consistency of using our NCD estimator to decide conditional independence. Together these results justify the proposed approach. Experimental results demonstrate the effectiveness of our method in causal discovery, as well as the advantages of using our NCD measure over kernel-based measures.

Contrastive ACE: Domain Generalization Through Alignment of Causal Mechanisms

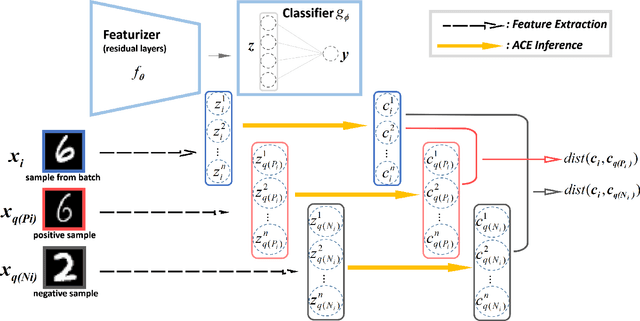
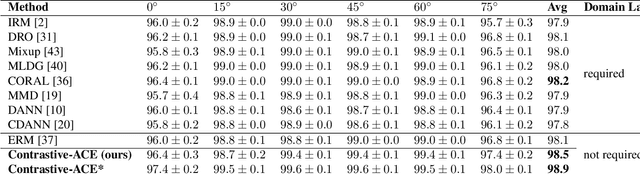
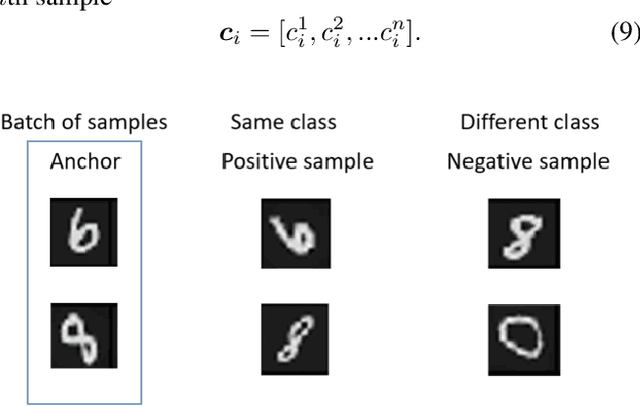
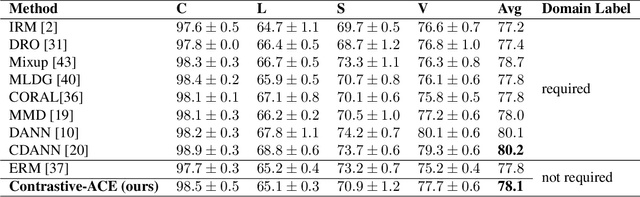
Domain generalization aims to learn knowledge invariant across different distributions while semantically meaningful for downstream tasks from multiple source domains, to improve the model's generalization ability on unseen target domains. The fundamental objective is to understand the underlying "invariance" behind these observational distributions and such invariance has been shown to have a close connection to causality. While many existing approaches make use of the property that causal features are invariant across domains, we consider the causal invariance of the average causal effect of the features to the labels. This invariance regularizes our training approach in which interventions are performed on features to enforce stability of the causal prediction by the classifier across domains. Our work thus sheds some light on the domain generalization problem by introducing invariance of the mechanisms into the learning process. Experiments on several benchmark datasets demonstrate the performance of the proposed method against SOTAs.

Clustering Causal Additive Noise Models

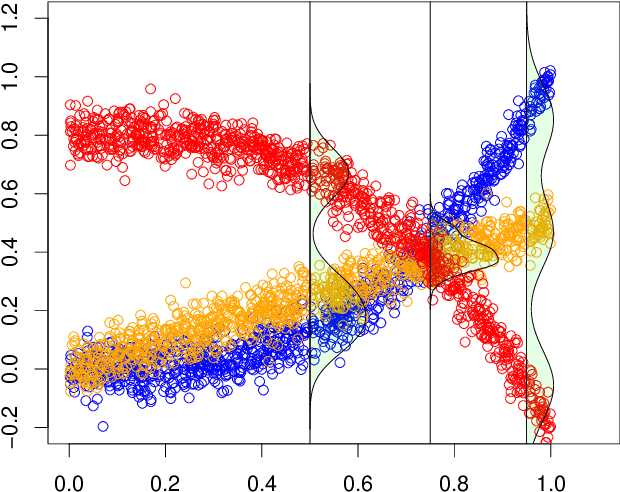
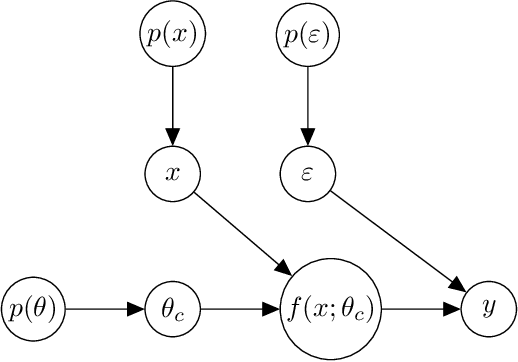
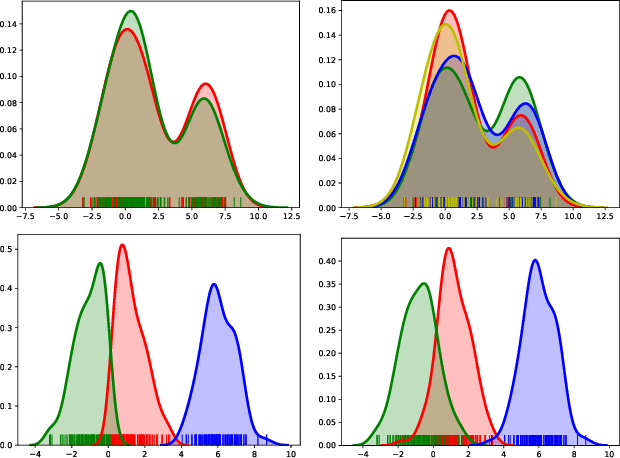
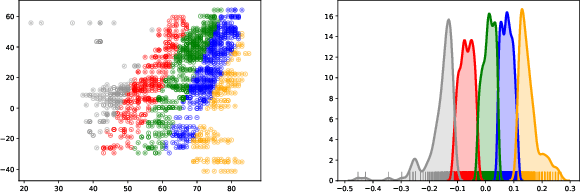
Additive noise models are commonly used to infer the causal direction for a given set of observed data. Most causal models assume a single homogeneous population. However, observations may be collected under different conditions in practice. Such data often require models that can accommodate possible heterogeneity caused by different conditions under which data have been collected. We propose a clustering algorithm inspired by the $k$-means algorithm, but with unknown $k$. Using the proposed algorithm, both the labels and the number of components are estimated from the collected data. The estimated labels are used to adjust the causal direction test statistic. The adjustment significantly improves the performance of the test statistic in identifying the correct causal direction.

Domain Generalization via Multidomain Discriminant Analysis

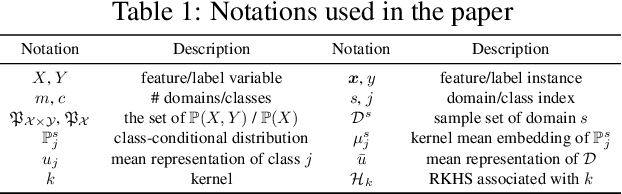
Domain generalization (DG) aims to incorporate knowledge from multiple source domains into a single model that could generalize well on unseen target domains. This problem is ubiquitous in practice since the distributions of the target data may rarely be identical to those of the source data. In this paper, we propose Multidomain Discriminant Analysis (MDA) to address DG of classification tasks in general situations. MDA learns a domain-invariant feature transformation that aims to achieve appealing properties, including a minimal divergence among domains within each class, a maximal separability among classes, and overall maximal compactness of all classes. Furthermore, we provide the bounds on excess risk and generalization error by learning theory analysis. Comprehensive experiments on synthetic and real benchmark datasets demonstrate the effectiveness of MDA.

Causal Inference and Mechanism Clustering of A Mixture of Additive Noise Models

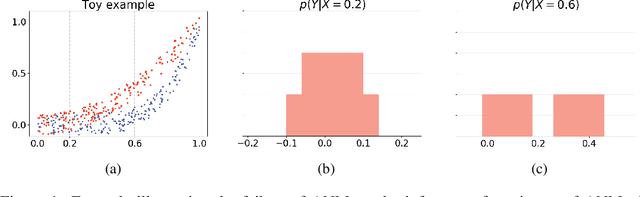
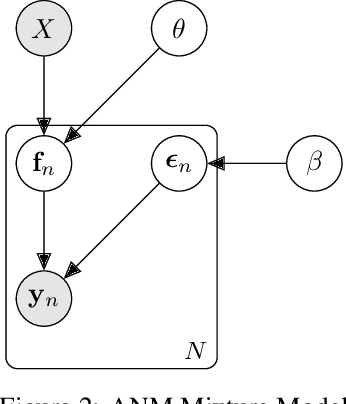
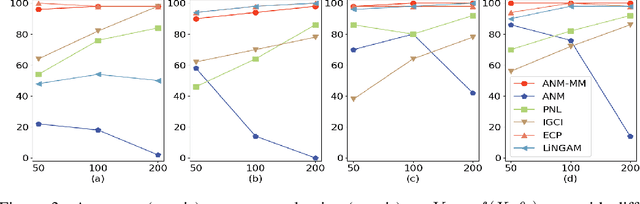
The inference of the causal relationship between a pair of observed variables is a fundamental problem in science, and most existing approaches are based on one single causal model. In practice, however, observations are often collected from multiple sources with heterogeneous causal models due to certain uncontrollable factors, which renders causal analysis results obtained by a single model skeptical. In this paper, we generalize the Additive Noise Model (ANM) to a mixture model, which consists of a finite number of ANMs, and provide the condition of its causal identifiability. To conduct model estimation, we propose Gaussian Process Partially Observable Model (GPPOM), and incorporate independence enforcement into it to learn latent parameter associated with each observation. Causal inference and clustering according to the underlying generating mechanisms of the mixture model are addressed in this work. Experiments on synthetic and real data demonstrate the effectiveness of our proposed approach.

A Kernel Embedding-based Approach for Nonstationary Causal Model Inference

Although nonstationary data are more common in the real world, most existing causal discovery methods do not take nonstationarity into consideration. In this letter, we propose a kernel embedding-based approach, ENCI, for nonstationary causal model inference where data are collected from multiple domains with varying distributions. In ENCI, we transform the complicated relation of a cause-effect pair into a linear model of variables of which observations correspond to the kernel embeddings of the cause-and-effect distributions in different domains. In this way, we are able to estimate the causal direction by exploiting the causal asymmetry of the transformed linear model. Furthermore, we extend ENCI to causal graph discovery for multiple variables by transforming the relations among them into a linear nongaussian acyclic model. We show that by exploiting the nonstationarity of distributions, both cause-effect pairs and two kinds of causal graphs are identifiable under mild conditions. Experiments on synthetic and real-world data are conducted to justify the efficacy of ENCI over major existing methods.