Causal Inference and Mechanism Clustering of A Mixture of Additive Noise Models
Paper and Code
Oct 27, 2018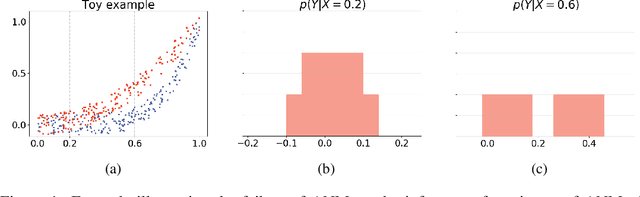

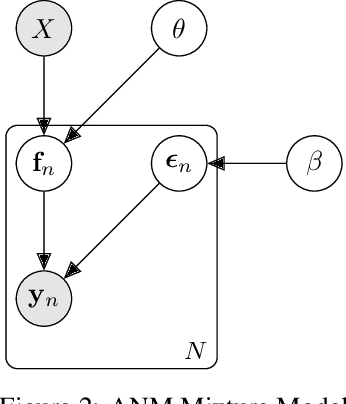
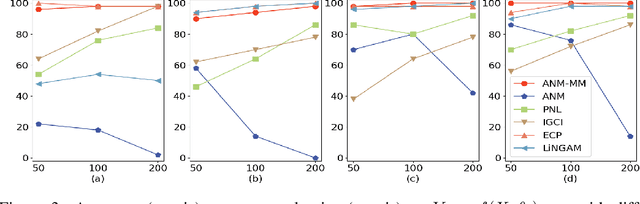
The inference of the causal relationship between a pair of observed variables is a fundamental problem in science, and most existing approaches are based on one single causal model. In practice, however, observations are often collected from multiple sources with heterogeneous causal models due to certain uncontrollable factors, which renders causal analysis results obtained by a single model skeptical. In this paper, we generalize the Additive Noise Model (ANM) to a mixture model, which consists of a finite number of ANMs, and provide the condition of its causal identifiability. To conduct model estimation, we propose Gaussian Process Partially Observable Model (GPPOM), and incorporate independence enforcement into it to learn latent parameter associated with each observation. Causal inference and clustering according to the underlying generating mechanisms of the mixture model are addressed in this work. Experiments on synthetic and real data demonstrate the effectiveness of our proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge