Domain Generalization via Multidomain Discriminant Analysis

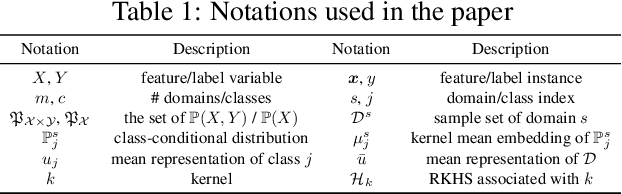
Domain generalization (DG) aims to incorporate knowledge from multiple source domains into a single model that could generalize well on unseen target domains. This problem is ubiquitous in practice since the distributions of the target data may rarely be identical to those of the source data. In this paper, we propose Multidomain Discriminant Analysis (MDA) to address DG of classification tasks in general situations. MDA learns a domain-invariant feature transformation that aims to achieve appealing properties, including a minimal divergence among domains within each class, a maximal separability among classes, and overall maximal compactness of all classes. Furthermore, we provide the bounds on excess risk and generalization error by learning theory analysis. Comprehensive experiments on synthetic and real benchmark datasets demonstrate the effectiveness of MDA.

Causal Inference and Mechanism Clustering of A Mixture of Additive Noise Models

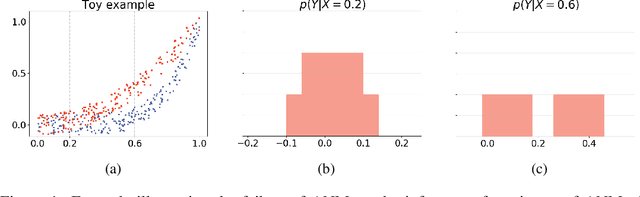
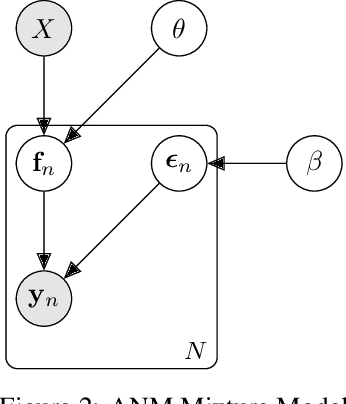
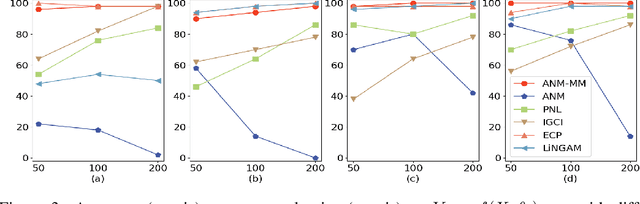
The inference of the causal relationship between a pair of observed variables is a fundamental problem in science, and most existing approaches are based on one single causal model. In practice, however, observations are often collected from multiple sources with heterogeneous causal models due to certain uncontrollable factors, which renders causal analysis results obtained by a single model skeptical. In this paper, we generalize the Additive Noise Model (ANM) to a mixture model, which consists of a finite number of ANMs, and provide the condition of its causal identifiability. To conduct model estimation, we propose Gaussian Process Partially Observable Model (GPPOM), and incorporate independence enforcement into it to learn latent parameter associated with each observation. Causal inference and clustering according to the underlying generating mechanisms of the mixture model are addressed in this work. Experiments on synthetic and real data demonstrate the effectiveness of our proposed approach.

A Kernel Embedding-based Approach for Nonstationary Causal Model Inference

Although nonstationary data are more common in the real world, most existing causal discovery methods do not take nonstationarity into consideration. In this letter, we propose a kernel embedding-based approach, ENCI, for nonstationary causal model inference where data are collected from multiple domains with varying distributions. In ENCI, we transform the complicated relation of a cause-effect pair into a linear model of variables of which observations correspond to the kernel embeddings of the cause-and-effect distributions in different domains. In this way, we are able to estimate the causal direction by exploiting the causal asymmetry of the transformed linear model. Furthermore, we extend ENCI to causal graph discovery for multiple variables by transforming the relations among them into a linear nongaussian acyclic model. We show that by exploiting the nonstationarity of distributions, both cause-effect pairs and two kinds of causal graphs are identifiable under mild conditions. Experiments on synthetic and real-world data are conducted to justify the efficacy of ENCI over major existing methods.

Causal Inference on Discrete Data via Estimating Distance Correlations

In this paper, we deal with the problem of inferring causal directions when the data is on discrete domain. By considering the distribution of the cause $P(X)$ and the conditional distribution mapping cause to effect $P(Y|X)$ as independent random variables, we propose to infer the causal direction via comparing the distance correlation between $P(X)$ and $P(Y|X)$ with the distance correlation between $P(Y)$ and $P(X|Y)$. We infer "$X$ causes $Y$" if the dependence coefficient between $P(X)$ and $P(Y|X)$ is smaller. Experiments are performed to show the performance of the proposed method.

Confounder Detection in High Dimensional Linear Models using First Moments of Spectral Measures

In this paper, we study the confounder detection problem in the linear model, where the target variable $Y$ is predicted using its $n$ potential causes $X_n=(x_1,...,x_n)^T$. Based on an assumption of rotation invariant generating process of the model, recent study shows that the spectral measure induced by the regression coefficient vector with respect to the covariance matrix of $X_n$ is close to a uniform measure in purely causal cases, but it differs from a uniform measure characteristically in the presence of a scalar confounder. Then, analyzing spectral measure pattern could help to detect confounding. In this paper, we propose to use the first moment of the spectral measure for confounder detection. We calculate the first moment of the regression vector induced spectral measure, and compare it with the first moment of a uniform spectral measure, both defined with respect to the covariance matrix of $X_n$. The two moments coincide in non-confounding cases, and differ from each other in the presence of confounding. This statistical causal-confounding asymmetry can be used for confounder detection. Without the need of analyzing the spectral measure pattern, our method does avoid the difficulty of metric choice and multiple parameter optimization. Experiments on synthetic and real data show the performance of this method.

Bridging Information Criteria and Parameter Shrinkage for Model Selection

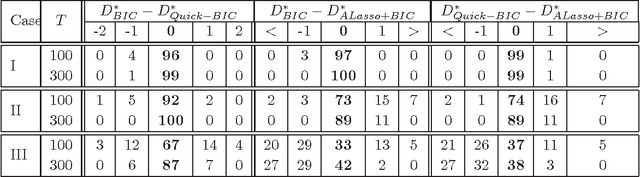
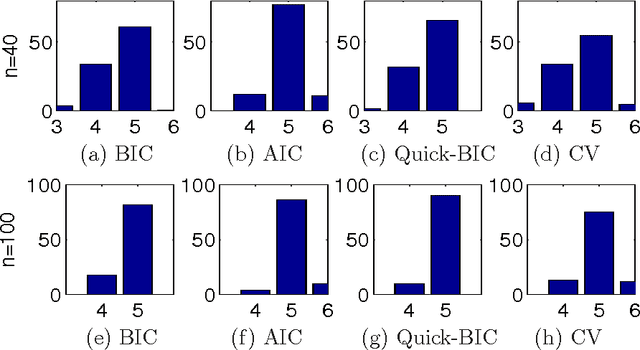
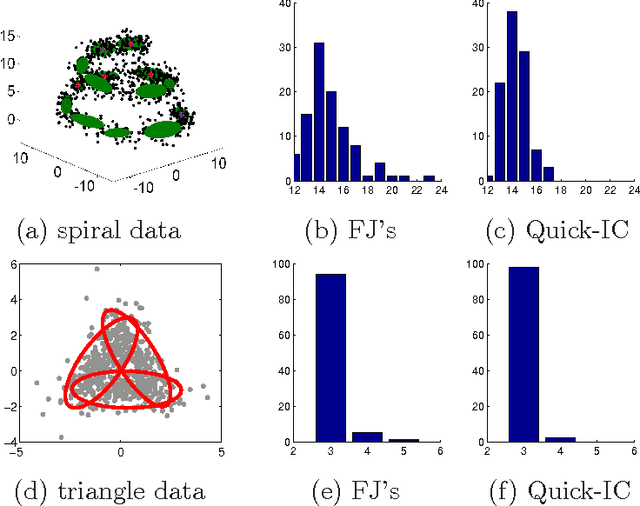
Model selection based on classical information criteria, such as BIC, is generally computationally demanding, but its properties are well studied. On the other hand, model selection based on parameter shrinkage by $\ell_1$-type penalties is computationally efficient. In this paper we make an attempt to combine their strengths, and propose a simple approach that penalizes the likelihood with data-dependent $\ell_1$ penalties as in adaptive Lasso and exploits a fixed penalization parameter. Even for finite samples, its model selection results approximately coincide with those based on information criteria; in particular, we show that in some special cases, this approach and the corresponding information criterion produce exactly the same model. One can also consider this approach as a way to directly determine the penalization parameter in adaptive Lasso to achieve information criteria-like model selection. As extensions, we apply this idea to complex models including Gaussian mixture model and mixture of factor analyzers, whose model selection is traditionally difficult to do; by adopting suitable penalties, we provide continuous approximators to the corresponding information criteria, which are easy to optimize and enable efficient model selection.