Model Free Prediction with Uncertainty Assessment

Deep nonparametric regression, characterized by the utilization of deep neural networks to learn target functions, has emerged as a focal point of research attention in recent years. Despite considerable progress in understanding convergence rates, the absence of asymptotic properties hinders rigorous statistical inference. To address this gap, we propose a novel framework that transforms the deep estimation paradigm into a platform conducive to conditional mean estimation, leveraging the conditional diffusion model. Theoretically, we develop an end-to-end convergence rate for the conditional diffusion model and establish the asymptotic normality of the generated samples. Consequently, we are equipped to construct confidence regions, facilitating robust statistical inference. Furthermore, through numerical experiments, we empirically validate the efficacy of our proposed methodology.

Bridging Information Criteria and Parameter Shrinkage for Model Selection

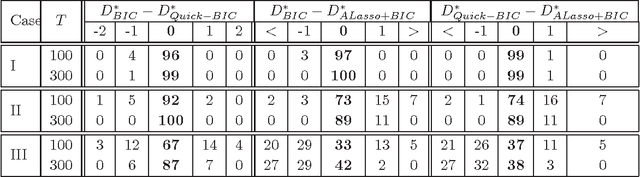
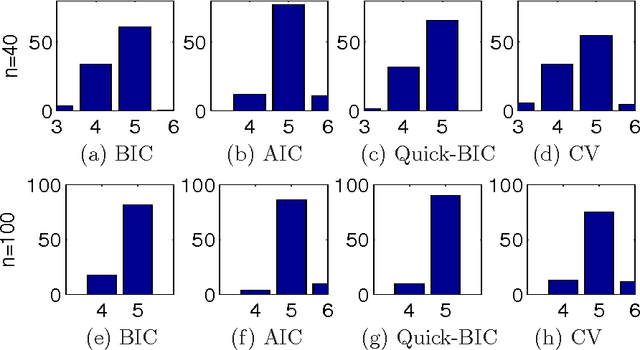
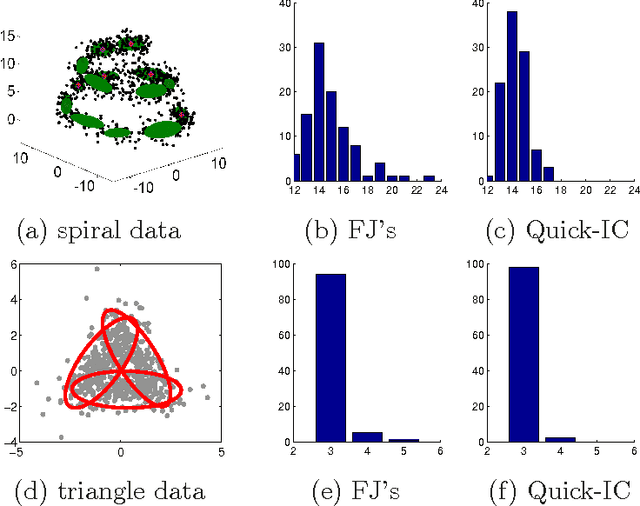
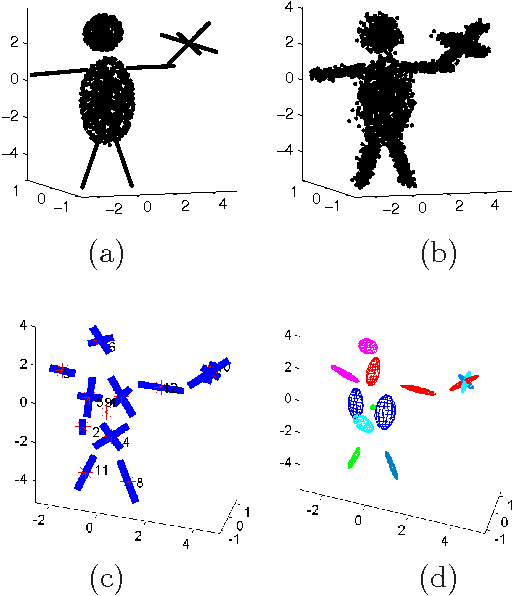
Model selection based on classical information criteria, such as BIC, is generally computationally demanding, but its properties are well studied. On the other hand, model selection based on parameter shrinkage by $\ell_1$-type penalties is computationally efficient. In this paper we make an attempt to combine their strengths, and propose a simple approach that penalizes the likelihood with data-dependent $\ell_1$ penalties as in adaptive Lasso and exploits a fixed penalization parameter. Even for finite samples, its model selection results approximately coincide with those based on information criteria; in particular, we show that in some special cases, this approach and the corresponding information criterion produce exactly the same model. One can also consider this approach as a way to directly determine the penalization parameter in adaptive Lasso to achieve information criteria-like model selection. As extensions, we apply this idea to complex models including Gaussian mixture model and mixture of factor analyzers, whose model selection is traditionally difficult to do; by adopting suitable penalties, we provide continuous approximators to the corresponding information criteria, which are easy to optimize and enable efficient model selection.

Model Selection for Gaussian Mixture Models

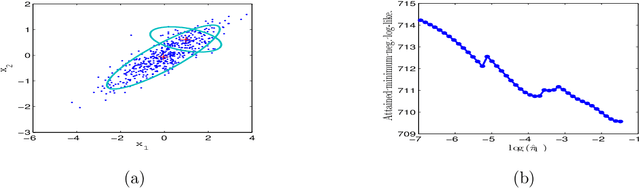
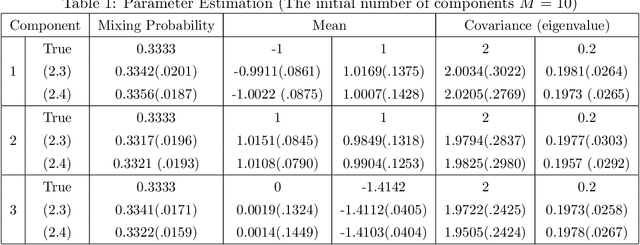
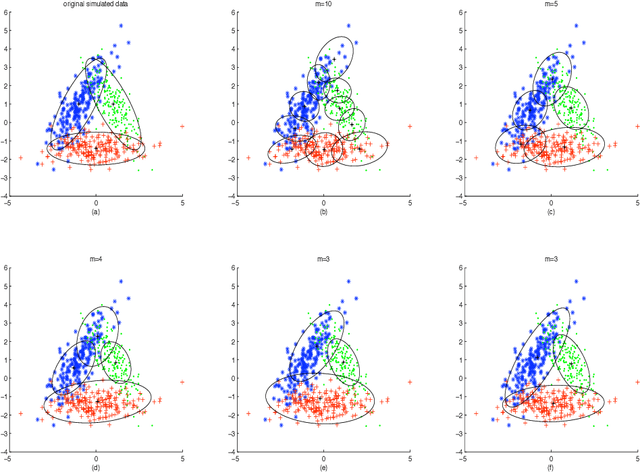
This paper is concerned with an important issue in finite mixture modelling, the selection of the number of mixing components. We propose a new penalized likelihood method for model selection of finite multivariate Gaussian mixture models. The proposed method is shown to be statistically consistent in determining of the number of components. A modified EM algorithm is developed to simultaneously select the number of components and to estimate the mixing weights, i.e. the mixing probabilities, and unknown parameters of Gaussian distributions. Simulations and a real data analysis are presented to illustrate the performance of the proposed method.