Provable benefits of annealing for estimating normalizing constants: Importance Sampling, Noise-Contrastive Estimation, and beyond

Recent research has developed several Monte Carlo methods for estimating the normalization constant (partition function) based on the idea of annealing. This means sampling successively from a path of distributions that interpolate between a tractable "proposal" distribution and the unnormalized "target" distribution. Prominent estimators in this family include annealed importance sampling and annealed noise-contrastive estimation (NCE). Such methods hinge on a number of design choices: which estimator to use, which path of distributions to use and whether to use a path at all; so far, there is no definitive theory on which choices are efficient. Here, we evaluate each design choice by the asymptotic estimation error it produces. First, we show that using NCE is more efficient than the importance sampling estimator, but in the limit of infinitesimal path steps, the difference vanishes. Second, we find that using the geometric path brings down the estimation error from an exponential to a polynomial function of the parameter distance between the target and proposal distributions. Third, we find that the arithmetic path, while rarely used, can offer optimality properties over the universally-used geometric path. In fact, in a particular limit, the optimal path is arithmetic. Based on this theory, we finally propose a two-step estimator to approximate the optimal path in an efficient way.

Nonlinear Independent Component Analysis for Principled Disentanglement in Unsupervised Deep Learning

A central problem in unsupervised deep learning is how to find useful representations of high-dimensional data, sometimes called "disentanglement". Most approaches are heuristic and lack a proper theoretical foundation. In linear representation learning, independent component analysis (ICA) has been successful in many applications areas, and it is principled, i.e. based on a well-defined probabilistic model. However, extension of ICA to the nonlinear case has been problematic due to the lack of identifiability, i.e. uniqueness of the representation. Recently, nonlinear extensions that utilize temporal structure or some auxiliary information have been proposed. Such models are in fact identifiable, and consequently, an increasing number of algorithms have been developed. In particular, some self-supervised algorithms can be shown to estimate nonlinear ICA, even though they have initially been proposed from heuristic perspectives. This paper reviews the state-of-the-art of nonlinear ICA theory and algorithms.

Optimizing the Noise in Self-Supervised Learning: from Importance Sampling to Noise-Contrastive Estimation

Self-supervised learning is an increasingly popular approach to unsupervised learning, achieving state-of-the-art results. A prevalent approach consists in contrasting data points and noise points within a classification task: this requires a good noise distribution which is notoriously hard to specify. While a comprehensive theory is missing, it is widely assumed that the optimal noise distribution should in practice be made equal to the data distribution, as in Generative Adversarial Networks (GANs). We here empirically and theoretically challenge this assumption. We turn to Noise-Contrastive Estimation (NCE) which grounds this self-supervised task as an estimation problem of an energy-based model of the data. This ties the optimality of the noise distribution to the sample efficiency of the estimator, which is rigorously defined as its asymptotic variance, or mean-squared error. In the special case where the normalization constant only is unknown, we show that NCE recovers a family of Importance Sampling estimators for which the optimal noise is indeed equal to the data distribution. However, in the general case where the energy is also unknown, we prove that the optimal noise density is the data density multiplied by a correction term based on the Fisher score. In particular, the optimal noise distribution is different from the data distribution, and is even from a different family. Nevertheless, we soberly conclude that the optimal noise may be hard to sample from, and the gain in efficiency can be modest compared to choosing the noise distribution equal to the data's.

The Optimal Noise in Noise-Contrastive Learning Is Not What You Think

Learning a parametric model of a data distribution is a well-known statistical problem that has seen renewed interest as it is brought to scale in deep learning. Framing the problem as a self-supervised task, where data samples are discriminated from noise samples, is at the core of state-of-the-art methods, beginning with Noise-Contrastive Estimation (NCE). Yet, such contrastive learning requires a good noise distribution, which is hard to specify; domain-specific heuristics are therefore widely used. While a comprehensive theory is missing, it is widely assumed that the optimal noise should in practice be made equal to the data, both in distribution and proportion. This setting underlies Generative Adversarial Networks (GANs) in particular. Here, we empirically and theoretically challenge this assumption on the optimal noise. We show that deviating from this assumption can actually lead to better statistical estimators, in terms of asymptotic variance. In particular, the optimal noise distribution is different from the data's and even from a different family.

Disentangling Identifiable Features from Noisy Data with Structured Nonlinear ICA

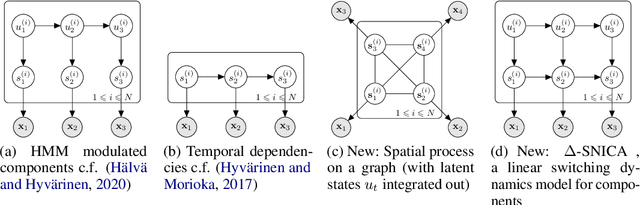
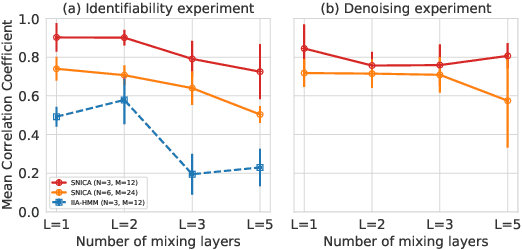
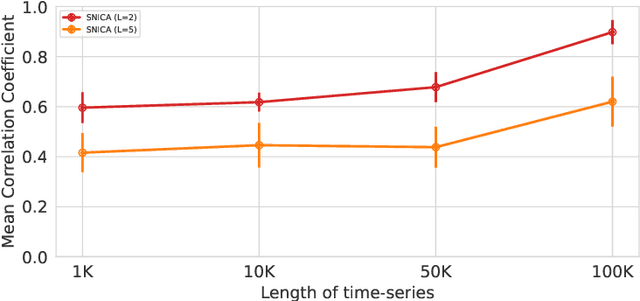
We introduce a new general identifiable framework for principled disentanglement referred to as Structured Nonlinear Independent Component Analysis (SNICA). Our contribution is to extend the identifiability theory of deep generative models for a very broad class of structured models. While previous works have shown identifiability for specific classes of time-series models, our theorems extend this to more general temporal structures as well as to models with more complex structures such as spatial dependencies. In particular, we establish the major result that identifiability for this framework holds even in the presence of noise of unknown distribution. The SNICA setting therefore subsumes all the existing nonlinear ICA models for time-series and also allows for new much richer identifiable models. Finally, as an example of our framework's flexibility, we introduce the first nonlinear ICA model for time-series that combines the following very useful properties: it accounts for both nonstationarity and autocorrelation in a fully unsupervised setting; performs dimensionality reduction; models hidden states; and enables principled estimation and inference by variational maximum-likelihood.

Autoregressive flow-based causal discovery and inference

We posit that autoregressive flow models are well-suited to performing a range of causal inference tasks - ranging from causal discovery to making interventional and counterfactual predictions. In particular, we exploit the fact that autoregressive architectures define an ordering over variables, analogous to a causal ordering, in order to propose a single flow architecture to perform all three aforementioned tasks. We first leverage the fact that flow models estimate normalized log-densities of data to derive a bivariate measure of causal direction based on likelihood ratios. Whilst traditional measures of causal direction often require restrictive assumptions on the nature of causal relationships (e.g., linearity),the flexibility of flow models allows for arbitrary causal dependencies. Our approach compares favourably against alternative methods on synthetic data as well as on the Cause-Effect Pairs bench-mark dataset. Subsequently, we demonstrate that the invertible nature of flows naturally allows for direct evaluation of both interventional and counterfactual predictions, which require marginalization and conditioning over latent variables respectively. We present examples over synthetic data where autoregressive flows, when trained under the correct causal ordering, are able to make accurate interventional and counterfactual predictions

Information criteria for non-normalized models

Many statistical models are given in the form of non-normalized densities with an intractable normalization constant. Since maximum likelihood estimation is computationally intensive for these models, several estimation methods have been developed which do not require explicit computation of the normalization constant, such as noise contrastive estimation (NCE) and score matching. However, model selection methods for general non-normalized models have not been proposed so far. In this study, we develop information criteria for non-normalized models estimated by NCE or score matching. They are derived as approximately unbiased estimators of discrepancy measures for non-normalized models. Experimental results demonstrate that the proposed criteria enable selection of the appropriate non-normalized model in a data-driven manner. Extension to a finite mixture of non-normalized models is also discussed.

Causal Discovery with General Non-Linear Relationships Using Non-Linear ICA

We consider the problem of inferring causal relationships between two or more passively observed variables. While the problem of such causal discovery has been extensively studied especially in the bivariate setting, the majority of current methods assume a linear causal relationship, and the few methods which consider non-linear dependencies usually make the assumption of additive noise. Here, we propose a framework through which we can perform causal discovery in the presence of general non-linear relationships. The proposed method is based on recent progress in non-linear independent component analysis and exploits the non-stationarity of observations in order to recover the underlying sources or latent disturbances. We show rigorously that in the case of bivariate causal discovery, such non-linear ICA can be used to infer the causal direction via a series of independence tests. We further propose an alternative measure of causal direction based on asymptotic approximations to the likelihood ratio, as well as an extension to multivariate causal discovery. We demonstrate the capabilities of the proposed method via a series of simulation studies and conclude with an application to neuroimaging data.

Neural Empirical Bayes

We formulate a novel framework that unifies kernel density estimation and empirical Bayes, where we address a broad set of problems in unsupervised learning with a geometric interpretation rooted in the concentration of measure phenomenon. We start by energy estimation based on a denoising objective which recovers the original/clean data X from its measured/noisy version Y with empirical Bayes least squares estimator. The setup is rooted in kernel density estimation, but the log-pdf in Y is parametrized with a neural network, and crucially, the learning objective is derived for any level of noise/kernel bandwidth. Learning is efficient with double backpropagation and stochastic gradient descent. An elegant physical picture emerges of an interacting system of high-dimensional spheres around each data point, together with a globally-defined probability flow field. The picture is powerful: it leads to a novel sampling algorithm, a new notion of associative memory, and it is instrumental in designing experiments. We start with extreme denoising experiments. Walk-jump sampling is defined by Langevin MCMC walks in Y, along with asynchronous empirical Bayes jumps to X. Robbins associative memory is defined by a deterministic flow to attractors of the learned probability flow field. Finally, we observed the emergence of remarkably rich creative modes in the regime of highly overlapping spheres.

Nonlinear ICA Using Auxiliary Variables and Generalized Contrastive Learning

Nonlinear ICA is a fundamental problem for unsupervised representation learning, emphasizing the capacity to recover the underlying latent variables generating the data (i.e., identifiability). Recently, the very first identifiability proofs for nonlinear ICA have been proposed, leveraging the temporal structure of the independent components. Here, we propose a general framework for nonlinear ICA, which, as a special case, can make use of temporal structure. It is based on augmenting the data by an auxiliary variable, such as the time index, the history of the time series, or any other available information. We propose to learn nonlinear ICA by discriminating between true augmented data, or data in which the auxiliary variable has been randomized. This enables the framework to be implemented algorithmically through logistic regression, possibly in a neural network. We provide a comprehensive proof of the identifiability of the model as well as the consistency of our estimation method. The approach not only provides a general theoretical framework combining and generalizing previously proposed nonlinear ICA models and algorithms, but also brings practical advantages.