Exploring Intra and Inter-language Consistency in Embeddings with ICA

Word embeddings represent words as multidimensional real vectors, facilitating data analysis and processing, but are often challenging to interpret. Independent Component Analysis (ICA) creates clearer semantic axes by identifying independent key features. Previous research has shown ICA's potential to reveal universal semantic axes across languages. However, it lacked verification of the consistency of independent components within and across languages. We investigated the consistency of semantic axes in two ways: both within a single language and across multiple languages. We first probed into intra-language consistency, focusing on the reproducibility of axes by performing ICA multiple times and clustering the outcomes. Then, we statistically examined inter-language consistency by verifying those axes' correspondences using statistical tests. We newly applied statistical methods to establish a robust framework that ensures the reliability and universality of semantic axes.

Information Geometry of Wasserstein Statistics on Shapes and Affine Deformations

Information geometry and Wasserstein geometry are two main structures introduced in a manifold of probability distributions, and they capture its different characteristics. We study characteristics of Wasserstein geometry in the framework of Li and Zhao (2023) for the affine deformation statistical model, which is a multi-dimensional generalization of the location-scale model. We compare merits and demerits of estimators based on information geometry and Wasserstein geometry. The shape of a probability distribution and its affine deformation are separated in the Wasserstein geometry, showing its robustness against the waveform perturbation in exchange for the loss in Fisher efficiency. We show that the Wasserstein estimator is the moment estimator in the case of the elliptically symmetric affine deformation model. It coincides with the information-geometrical estimator (maximum-likelihood estimator) when and only when the waveform is Gaussian. The role of the Wasserstein efficiency is elucidated in terms of robustness against waveform change.

Inadmissibility of the corrected Akaike information criterion

For the multivariate linear regression model with unknown covariance, the corrected Akaike information criterion is the minimum variance unbiased estimator of the expected Kullback--Leibler discrepancy. In this study, based on the loss estimation framework, we show its inadmissibility as an estimator of the Kullback--Leibler discrepancy itself, instead of the expected Kullback--Leibler discrepancy. We provide improved estimators of the Kullback--Leibler discrepancy that work well in reduced-rank situations and examine their performance numerically.

Information criteria for non-normalized models

Many statistical models are given in the form of non-normalized densities with an intractable normalization constant. Since maximum likelihood estimation is computationally intensive for these models, several estimation methods have been developed which do not require explicit computation of the normalization constant, such as noise contrastive estimation (NCE) and score matching. However, model selection methods for general non-normalized models have not been proposed so far. In this study, we develop information criteria for non-normalized models estimated by NCE or score matching. They are derived as approximately unbiased estimators of discrepancy measures for non-normalized models. Experimental results demonstrate that the proposed criteria enable selection of the appropriate non-normalized model in a data-driven manner. Extension to a finite mixture of non-normalized models is also discussed.

Imputation estimators for unnormalized models with missing data

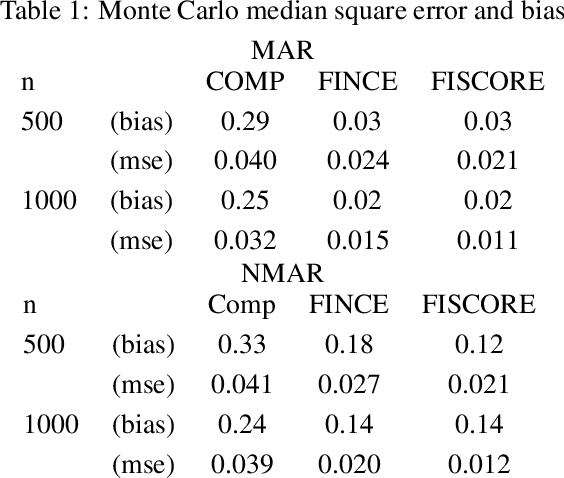
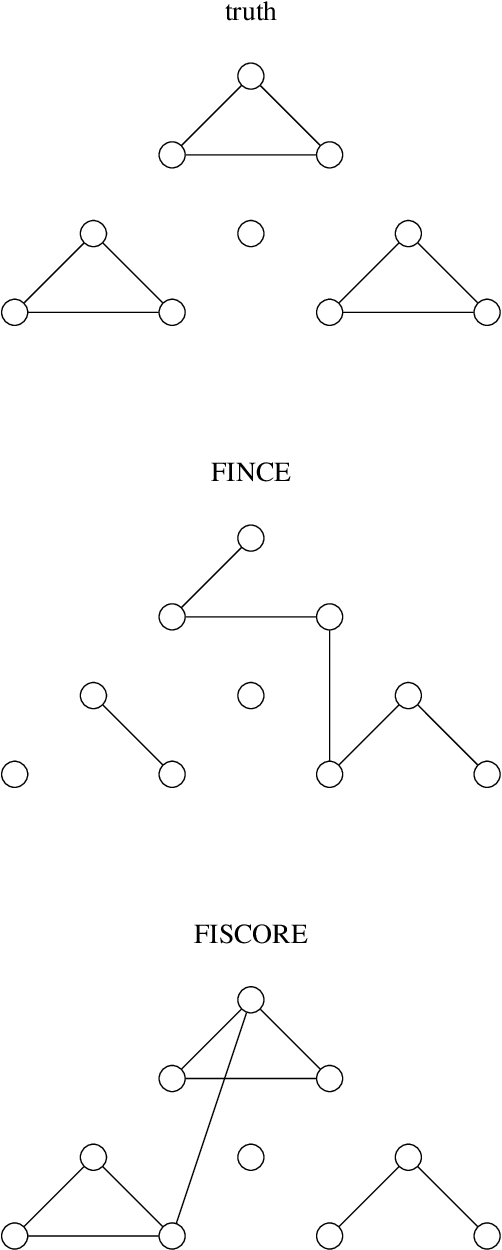
We propose estimation methods for unnormalized models with missing data. The key concept is to combine a modern imputation technique with estimators for unnormalized models including noise contrastive estimation and score matching. Further, we derive asymptotic distributions of the proposed estimators and construct the confidence intervals. The application to truncated Gaussian graphical models with missing data shows the validity of the proposed methods.

Unified estimation framework for unnormalized models with statistical efficiency

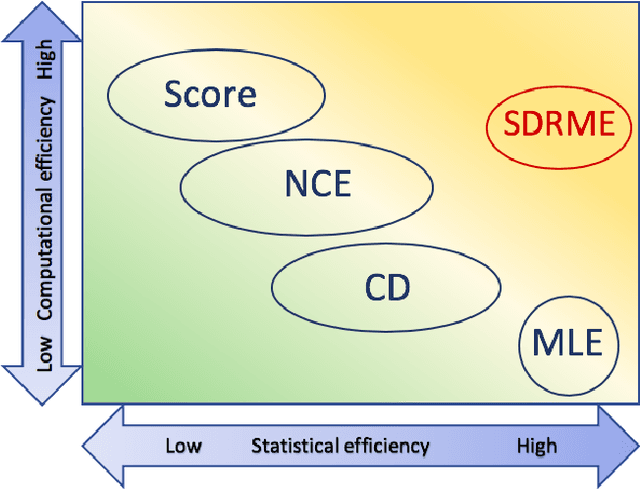
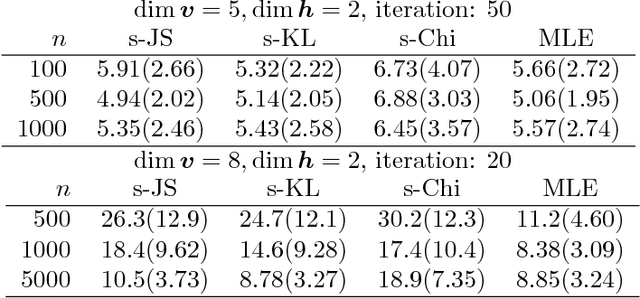
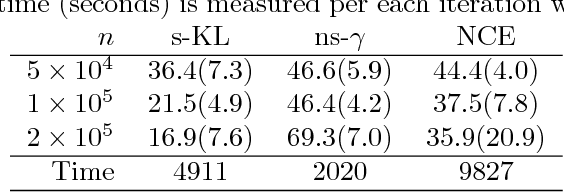
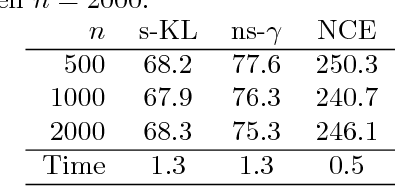
Parameter estimation of unnormalized models is a challenging problem because normalizing constants are not calculated explicitly and maximum likelihood estimation is computationally infeasible. Although some consistent estimators have been proposed earlier, the problem of statistical efficiency does remain. In this study, we propose a unified, statistically efficient estimation framework for unnormalized models and several novel efficient estimators with reasonable computational time regardless of whether the sample space is discrete or continuous. The loss functions of the proposed estimators are derived by combining the following two methods: (1) density-ratio matching using Bregman divergence, and (2) plugging-in nonparametric estimators. We also analyze the properties of the proposed estimators when the unnormalized model is misspecified. Finally, the experimental results demonstrate the advantages of our method over existing approaches.

Analysis of Noise Contrastive Estimation from the Perspective of Asymptotic Variance

There are many models, often called unnormalized models, whose normalizing constants are not calculated in closed form. Maximum likelihood estimation is not directly applicable to unnormalized models. Score matching, contrastive divergence method, pseudo-likelihood, Monte Carlo maximum likelihood, and noise contrastive estimation (NCE) are popular methods for estimating parameters of such models. In this paper, we focus on NCE. The estimator derived from NCE is consistent and asymptotically normal because it is an M-estimator. NCE characteristically uses an auxiliary distribution to calculate the normalizing constant in the same spirit of the importance sampling. In addition, there are several candidates as objective functions of NCE. We focus on how to reduce asymptotic variance. First, we propose a method for reducing asymptotic variance by estimating the parameters of the auxiliary distribution. Then, we determine the form of the objective functions, where the asymptotic variance takes the smallest values in the original estimator class and the proposed estimator classes. We further analyze the robustness of the estimator.

Estimation of Non-Normalized Mixture Models and Clustering Using Deep Representation

We develop a general method for estimating a finite mixture of non-normalized models. Here, a non-normalized model is defined to be a parametric distribution with an intractable normalization constant. Existing methods for estimating non-normalized models without computing the normalization constant are not applicable to mixture models because they contain more than one intractable normalization constant. The proposed method is derived by extending noise contrastive estimation (NCE), which estimates non-normalized models by discriminating between the observed data and some artificially generated noise. We also propose an extension of NCE with multiple noise distributions. Then, based on the observation that conventional classification learning with neural networks is implicitly assuming an exponential family as a generative model, we introduce a method for clustering unlabeled data by estimating a finite mixture of distributions in an exponential family. Estimation of this mixture model is attained by the proposed extensions of NCE where the training data of neural networks are used as noise. Thus, the proposed method provides a probabilistically principled clustering method that is able to utilize a deep representation. Application to image clustering using a deep neural network gives promising results.

Empirical Bayes Matrix Completion

We develop an empirical Bayes (EB) algorithm for the matrix completion problems. The EB algorithm is motivated from the singular value shrinkage estimator for matrix means by Efron and Morris (1972). Since the EB algorithm is essentially the EM algorithm applied to a simple model, it does not require heuristic parameter tuning other than tolerance. Numerical results demonstrated that the EB algorithm achieves a good trade-off between accuracy and efficiency compared to existing algorithms and that it works particularly well when the difference between the number of rows and columns is large. Application to real data also shows the practical utility of the EB algorithm.