Dynamic Search for Inference-Time Alignment in Diffusion Models

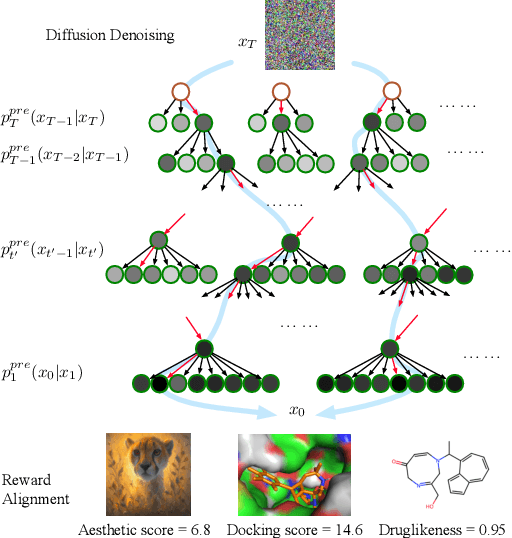
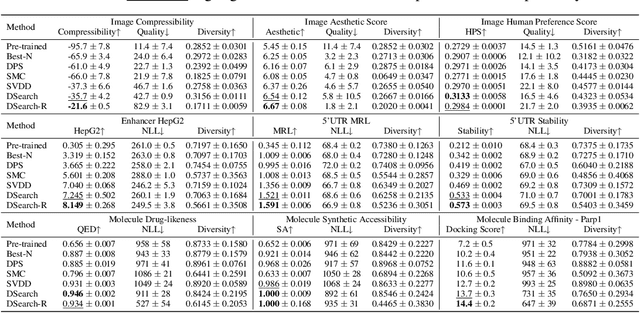
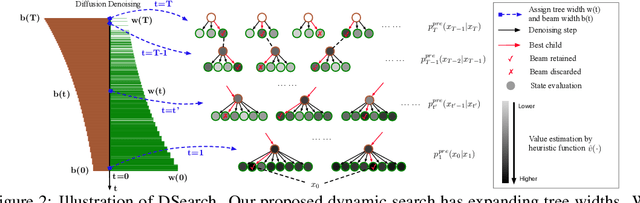
Diffusion models have shown promising generative capabilities across diverse domains, yet aligning their outputs with desired reward functions remains a challenge, particularly in cases where reward functions are non-differentiable. Some gradient-free guidance methods have been developed, but they often struggle to achieve optimal inference-time alignment. In this work, we newly frame inference-time alignment in diffusion as a search problem and propose Dynamic Search for Diffusion (DSearch), which subsamples from denoising processes and approximates intermediate node rewards. It also dynamically adjusts beam width and tree expansion to efficiently explore high-reward generations. To refine intermediate decisions, DSearch incorporates adaptive scheduling based on noise levels and a lookahead heuristic function. We validate DSearch across multiple domains, including biological sequence design, molecular optimization, and image generation, demonstrating superior reward optimization compared to existing approaches.

Reward-Guided Iterative Refinement in Diffusion Models at Test-Time with Applications to Protein and DNA Design

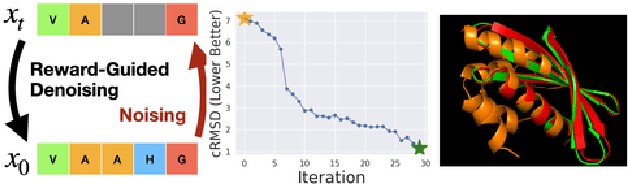
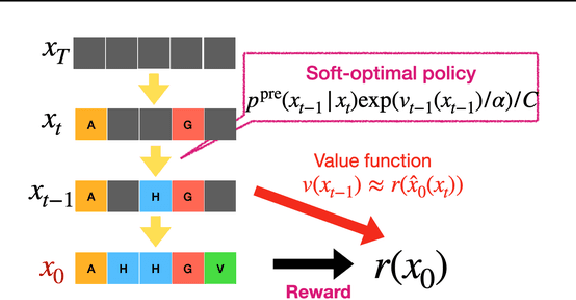
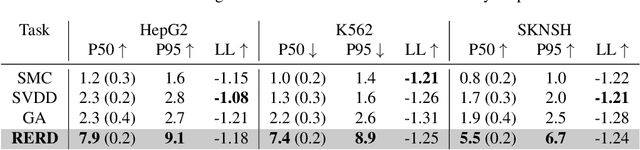
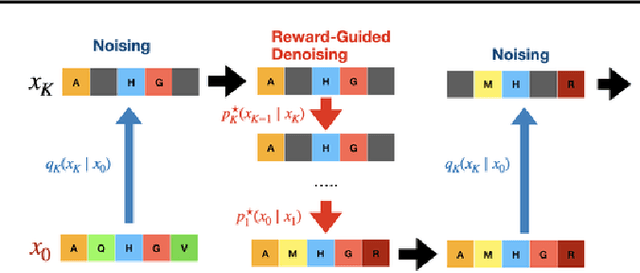
To fully leverage the capabilities of diffusion models, we are often interested in optimizing downstream reward functions during inference. While numerous algorithms for reward-guided generation have been recently proposed due to their significance, current approaches predominantly focus on single-shot generation, transitioning from fully noised to denoised states. We propose a novel framework for inference-time reward optimization with diffusion models inspired by evolutionary algorithms. Our approach employs an iterative refinement process consisting of two steps in each iteration: noising and reward-guided denoising. This sequential refinement allows for the gradual correction of errors introduced during reward optimization. Besides, we provide a theoretical guarantee for our framework. Finally, we demonstrate its superior empirical performance in protein and cell-type-specific regulatory DNA design. The code is available at \href{https://github.com/masa-ue/ProDifEvo-Refinement}{https://github.com/masa-ue/ProDifEvo-Refinement}.

Reward-Guided Controlled Generation for Inference-Time Alignment in Diffusion Models: Tutorial and Review

This tutorial provides an in-depth guide on inference-time guidance and alignment methods for optimizing downstream reward functions in diffusion models. While diffusion models are renowned for their generative modeling capabilities, practical applications in fields such as biology often require sample generation that maximizes specific metrics (e.g., stability, affinity in proteins, closeness to target structures). In these scenarios, diffusion models can be adapted not only to generate realistic samples but also to explicitly maximize desired measures at inference time without fine-tuning. This tutorial explores the foundational aspects of such inference-time algorithms. We review these methods from a unified perspective, demonstrating that current techniques -- such as Sequential Monte Carlo (SMC)-based guidance, value-based sampling, and classifier guidance -- aim to approximate soft optimal denoising processes (a.k.a. policies in RL) that combine pre-trained denoising processes with value functions serving as look-ahead functions that predict from intermediate states to terminal rewards. Within this framework, we present several novel algorithms not yet covered in the literature. Furthermore, we discuss (1) fine-tuning methods combined with inference-time techniques, (2) inference-time algorithms based on search algorithms such as Monte Carlo tree search, which have received limited attention in current research, and (3) connections between inference-time algorithms in language models and diffusion models. The code of this tutorial on protein design is available at https://github.com/masa-ue/AlignInversePro

Fine-Tuning Discrete Diffusion Models via Reward Optimization with Applications to DNA and Protein Design

Recent studies have demonstrated the strong empirical performance of diffusion models on discrete sequences across domains from natural language to biological sequence generation. For example, in the protein inverse folding task, conditional diffusion models have achieved impressive results in generating natural-like sequences that fold back into the original structure. However, practical design tasks often require not only modeling a conditional distribution but also optimizing specific task objectives. For instance, we may prefer protein sequences with high stability. To address this, we consider the scenario where we have pre-trained discrete diffusion models that can generate natural-like sequences, as well as reward models that map sequences to task objectives. We then formulate the reward maximization problem within discrete diffusion models, analogous to reinforcement learning (RL), while minimizing the KL divergence against pretrained diffusion models to preserve naturalness. To solve this RL problem, we propose a novel algorithm, DRAKES, that enables direct backpropagation of rewards through entire trajectories generated by diffusion models, by making the originally non-differentiable trajectories differentiable using the Gumbel-Softmax trick. Our theoretical analysis indicates that our approach can generate sequences that are both natural-like and yield high rewards. While similar tasks have been recently explored in diffusion models for continuous domains, our work addresses unique algorithmic and theoretical challenges specific to discrete diffusion models, which arise from their foundation in continuous-time Markov chains rather than Brownian motion. Finally, we demonstrate the effectiveness of DRAKES in generating DNA and protein sequences that optimize enhancer activity and protein stability, respectively, important tasks for gene therapies and protein-based therapeutics.

Derivative-Free Guidance in Continuous and Discrete Diffusion Models with Soft Value-Based Decoding

Diffusion models excel at capturing the natural design spaces of images, molecules, DNA, RNA, and protein sequences. However, rather than merely generating designs that are natural, we often aim to optimize downstream reward functions while preserving the naturalness of these design spaces. Existing methods for achieving this goal often require ``differentiable'' proxy models (\textit{e.g.}, classifier guidance or DPS) or involve computationally expensive fine-tuning of diffusion models (\textit{e.g.}, classifier-free guidance, RL-based fine-tuning). In our work, we propose a new method to address these challenges. Our algorithm is an iterative sampling method that integrates soft value functions, which looks ahead to how intermediate noisy states lead to high rewards in the future, into the standard inference procedure of pre-trained diffusion models. Notably, our approach avoids fine-tuning generative models and eliminates the need to construct differentiable models. This enables us to (1) directly utilize non-differentiable features/reward feedback, commonly used in many scientific domains, and (2) apply our method to recent discrete diffusion models in a principled way. Finally, we demonstrate the effectiveness of our algorithm across several domains, including image generation, molecule generation, and DNA/RNA sequence generation. The code is available at \href{https://github.com/masa-ue/SVDD}{https://github.com/masa-ue/SVDD}.

Understanding Reinforcement Learning-Based Fine-Tuning of Diffusion Models: A Tutorial and Review

This tutorial provides a comprehensive survey of methods for fine-tuning diffusion models to optimize downstream reward functions. While diffusion models are widely known to provide excellent generative modeling capability, practical applications in domains such as biology require generating samples that maximize some desired metric (e.g., translation efficiency in RNA, docking score in molecules, stability in protein). In these cases, the diffusion model can be optimized not only to generate realistic samples but also to explicitly maximize the measure of interest. Such methods are based on concepts from reinforcement learning (RL). We explain the application of various RL algorithms, including PPO, differentiable optimization, reward-weighted MLE, value-weighted sampling, and path consistency learning, tailored specifically for fine-tuning diffusion models. We aim to explore fundamental aspects such as the strengths and limitations of different RL-based fine-tuning algorithms across various scenarios, the benefits of RL-based fine-tuning compared to non-RL-based approaches, and the formal objectives of RL-based fine-tuning (target distributions). Additionally, we aim to examine their connections with related topics such as classifier guidance, Gflownets, flow-based diffusion models, path integral control theory, and sampling from unnormalized distributions such as MCMC. The code of this tutorial is available at https://github.com/masa-ue/RLfinetuning_Diffusion_Bioseq

Adding Conditional Control to Diffusion Models with Reinforcement Learning

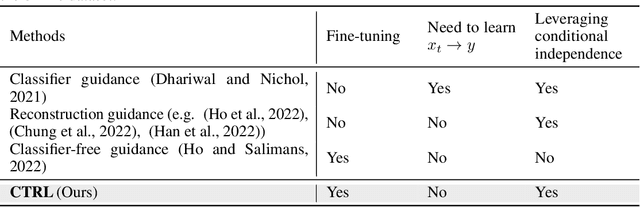
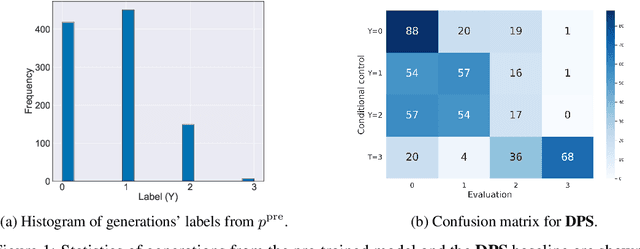
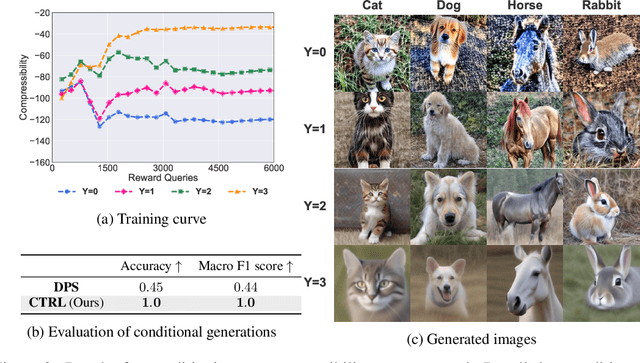
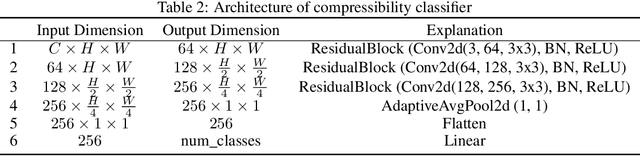
Diffusion models are powerful generative models that allow for precise control over the characteristics of the generated samples. While these diffusion models trained on large datasets have achieved success, there is often a need to introduce additional controls in downstream fine-tuning processes, treating these powerful models as pre-trained diffusion models. This work presents a novel method based on reinforcement learning (RL) to add additional controls, leveraging an offline dataset comprising inputs and corresponding labels. We formulate this task as an RL problem, with the classifier learned from the offline dataset and the KL divergence against pre-trained models serving as the reward functions. We introduce our method, $\textbf{CTRL}$ ($\textbf{C}$onditioning pre-$\textbf{T}$rained diffusion models with $\textbf{R}$einforcement $\textbf{L}$earning), which produces soft-optimal policies that maximize the abovementioned reward functions. We formally demonstrate that our method enables sampling from the conditional distribution conditioned on additional controls during inference. Our RL-based approach offers several advantages over existing methods. Compared to commonly used classifier-free guidance, our approach improves sample efficiency, and can greatly simplify offline dataset construction by exploiting conditional independence between the inputs and additional controls. Furthermore, unlike classifier guidance, we avoid the need to train classifiers from intermediate states to additional controls.

Bridging Model-Based Optimization and Generative Modeling via Conservative Fine-Tuning of Diffusion Models

AI-driven design problems, such as DNA/protein sequence design, are commonly tackled from two angles: generative modeling, which efficiently captures the feasible design space (e.g., natural images or biological sequences), and model-based optimization, which utilizes reward models for extrapolation. To combine the strengths of both approaches, we adopt a hybrid method that fine-tunes cutting-edge diffusion models by optimizing reward models through RL. Although prior work has explored similar avenues, they primarily focus on scenarios where accurate reward models are accessible. In contrast, we concentrate on an offline setting where a reward model is unknown, and we must learn from static offline datasets, a common scenario in scientific domains. In offline scenarios, existing approaches tend to suffer from overoptimization, as they may be misled by the reward model in out-of-distribution regions. To address this, we introduce a conservative fine-tuning approach, BRAID, by optimizing a conservative reward model, which includes additional penalization outside of offline data distributions. Through empirical and theoretical analysis, we demonstrate the capability of our approach to outperform the best designs in offline data, leveraging the extrapolation capabilities of reward models while avoiding the generation of invalid designs through pre-trained diffusion models.

Regularized DeepIV with Model Selection

In this paper, we study nonparametric estimation of instrumental variable (IV) regressions. While recent advancements in machine learning have introduced flexible methods for IV estimation, they often encounter one or more of the following limitations: (1) restricting the IV regression to be uniquely identified; (2) requiring minimax computation oracle, which is highly unstable in practice; (3) absence of model selection procedure. In this paper, we present the first method and analysis that can avoid all three limitations, while still enabling general function approximation. Specifically, we propose a minimax-oracle-free method called Regularized DeepIV (RDIV) regression that can converge to the least-norm IV solution. Our method consists of two stages: first, we learn the conditional distribution of covariates, and by utilizing the learned distribution, we learn the estimator by minimizing a Tikhonov-regularized loss function. We further show that our method allows model selection procedures that can achieve the oracle rates in the misspecified regime. When extended to an iterative estimator, our method matches the current state-of-the-art convergence rate. Our method is a Tikhonov regularized variant of the popular DeepIV method with a non-parametric MLE first-stage estimator, and our results provide the first rigorous guarantees for this empirically used method, showcasing the importance of regularization which was absent from the original work.

Fine-Tuning of Continuous-Time Diffusion Models as Entropy-Regularized Control

Diffusion models excel at capturing complex data distributions, such as those of natural images and proteins. While diffusion models are trained to represent the distribution in the training dataset, we often are more concerned with other properties, such as the aesthetic quality of the generated images or the functional properties of generated proteins. Diffusion models can be finetuned in a goal-directed way by maximizing the value of some reward function (e.g., the aesthetic quality of an image). However, these approaches may lead to reduced sample diversity, significant deviations from the training data distribution, and even poor sample quality due to the exploitation of an imperfect reward function. The last issue often occurs when the reward function is a learned model meant to approximate a ground-truth "genuine" reward, as is the case in many practical applications. These challenges, collectively termed "reward collapse," pose a substantial obstacle. To address this reward collapse, we frame the finetuning problem as entropy-regularized control against the pretrained diffusion model, i.e., directly optimizing entropy-enhanced rewards with neural SDEs. We present theoretical and empirical evidence that demonstrates our framework is capable of efficiently generating diverse samples with high genuine rewards, mitigating the overoptimization of imperfect reward models.