Aviv Regev
Joint Embedding vs Reconstruction: Provable Benefits of Latent Space Prediction for Self Supervised Learning
May 18, 2025



Abstract:Reconstruction and joint embedding have emerged as two leading paradigms in Self Supervised Learning (SSL). Reconstruction methods focus on recovering the original sample from a different view in input space. On the other hand, joint embedding methods align the representations of different views in latent space. Both approaches offer compelling advantages, yet practitioners lack clear guidelines for choosing between them. In this work, we unveil the core mechanisms that distinguish each paradigm. By leveraging closed form solutions for both approaches, we precisely characterize how the view generation process, e.g. data augmentation, impacts the learned representations. We then demonstrate that, unlike supervised learning, both SSL paradigms require a minimal alignment between augmentations and irrelevant features to achieve asymptotic optimality with increasing sample size. Our findings indicate that in scenarios where these irrelevant features have a large magnitude, joint embedding methods are preferable because they impose a strictly weaker alignment condition compared to reconstruction based methods. These results not only clarify the trade offs between the two paradigms but also substantiate the empirical success of joint embedding approaches on real world challenging datasets.
Dynamic Search for Inference-Time Alignment in Diffusion Models
Mar 03, 2025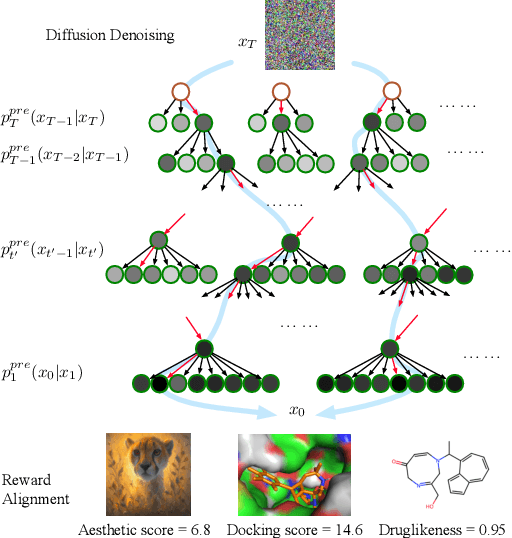
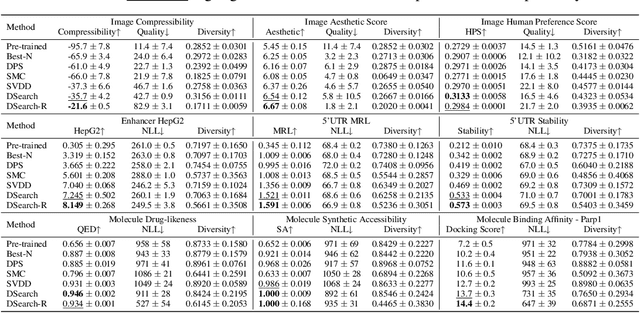
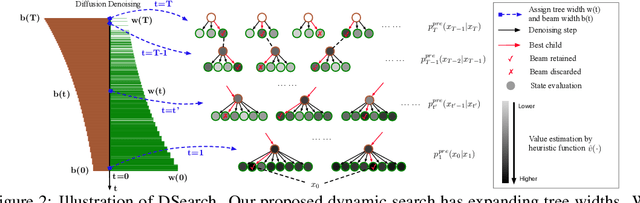

Abstract:Diffusion models have shown promising generative capabilities across diverse domains, yet aligning their outputs with desired reward functions remains a challenge, particularly in cases where reward functions are non-differentiable. Some gradient-free guidance methods have been developed, but they often struggle to achieve optimal inference-time alignment. In this work, we newly frame inference-time alignment in diffusion as a search problem and propose Dynamic Search for Diffusion (DSearch), which subsamples from denoising processes and approximates intermediate node rewards. It also dynamically adjusts beam width and tree expansion to efficiently explore high-reward generations. To refine intermediate decisions, DSearch incorporates adaptive scheduling based on noise levels and a lookahead heuristic function. We validate DSearch across multiple domains, including biological sequence design, molecular optimization, and image generation, demonstrating superior reward optimization compared to existing approaches.
Reward-Guided Iterative Refinement in Diffusion Models at Test-Time with Applications to Protein and DNA Design
Feb 20, 2025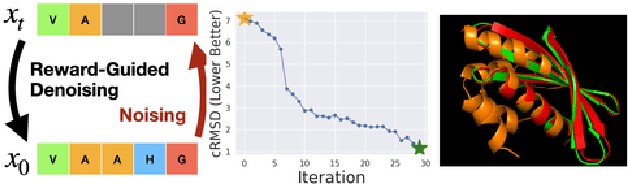
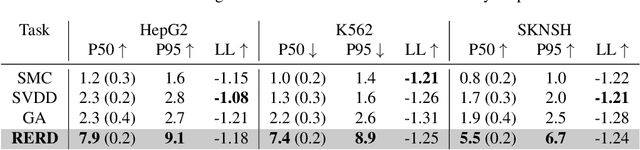
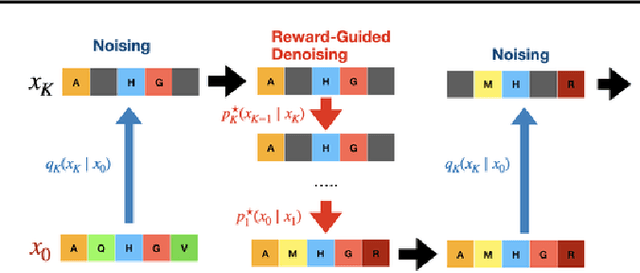
Abstract:To fully leverage the capabilities of diffusion models, we are often interested in optimizing downstream reward functions during inference. While numerous algorithms for reward-guided generation have been recently proposed due to their significance, current approaches predominantly focus on single-shot generation, transitioning from fully noised to denoised states. We propose a novel framework for inference-time reward optimization with diffusion models inspired by evolutionary algorithms. Our approach employs an iterative refinement process consisting of two steps in each iteration: noising and reward-guided denoising. This sequential refinement allows for the gradual correction of errors introduced during reward optimization. Besides, we provide a theoretical guarantee for our framework. Finally, we demonstrate its superior empirical performance in protein and cell-type-specific regulatory DNA design. The code is available at \href{https://github.com/masa-ue/ProDifEvo-Refinement}{https://github.com/masa-ue/ProDifEvo-Refinement}.
Supervised Contrastive Block Disentanglement
Feb 11, 2025



Abstract:Real-world datasets often combine data collected under different experimental conditions. This yields larger datasets, but also introduces spurious correlations that make it difficult to model the phenomena of interest. We address this by learning two embeddings to independently represent the phenomena of interest and the spurious correlations. The embedding representing the phenomena of interest is correlated with the target variable $y$, and is invariant to the environment variable $e$. In contrast, the embedding representing the spurious correlations is correlated with $e$. The invariance to $e$ is difficult to achieve on real-world datasets. Our primary contribution is an algorithm called Supervised Contrastive Block Disentanglement (SCBD) that effectively enforces this invariance. It is based purely on Supervised Contrastive Learning, and applies to real-world data better than existing approaches. We empirically validate SCBD on two challenging problems. The first problem is domain generalization, where we achieve strong performance on a synthetic dataset, as well as on Camelyon17-WILDS. We introduce a single hyperparameter $\alpha$ to control the degree of invariance to $e$. When we increase $\alpha$ to strengthen the degree of invariance, out-of-distribution performance improves at the expense of in-distribution performance. The second problem is batch correction, in which we apply SCBD to preserve biological signal and remove inter-well batch effects when modeling single-cell perturbations from 26 million Optical Pooled Screening images.
Reward-Guided Controlled Generation for Inference-Time Alignment in Diffusion Models: Tutorial and Review
Jan 16, 2025



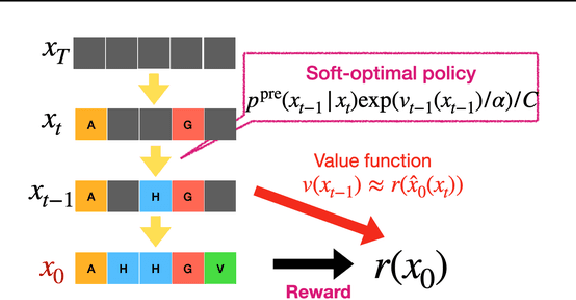
Abstract:This tutorial provides an in-depth guide on inference-time guidance and alignment methods for optimizing downstream reward functions in diffusion models. While diffusion models are renowned for their generative modeling capabilities, practical applications in fields such as biology often require sample generation that maximizes specific metrics (e.g., stability, affinity in proteins, closeness to target structures). In these scenarios, diffusion models can be adapted not only to generate realistic samples but also to explicitly maximize desired measures at inference time without fine-tuning. This tutorial explores the foundational aspects of such inference-time algorithms. We review these methods from a unified perspective, demonstrating that current techniques -- such as Sequential Monte Carlo (SMC)-based guidance, value-based sampling, and classifier guidance -- aim to approximate soft optimal denoising processes (a.k.a. policies in RL) that combine pre-trained denoising processes with value functions serving as look-ahead functions that predict from intermediate states to terminal rewards. Within this framework, we present several novel algorithms not yet covered in the literature. Furthermore, we discuss (1) fine-tuning methods combined with inference-time techniques, (2) inference-time algorithms based on search algorithms such as Monte Carlo tree search, which have received limited attention in current research, and (3) connections between inference-time algorithms in language models and diffusion models. The code of this tutorial on protein design is available at https://github.com/masa-ue/AlignInversePro
Fine-Tuning Discrete Diffusion Models via Reward Optimization with Applications to DNA and Protein Design
Oct 17, 2024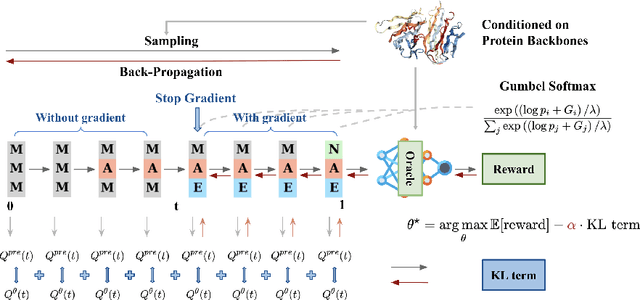
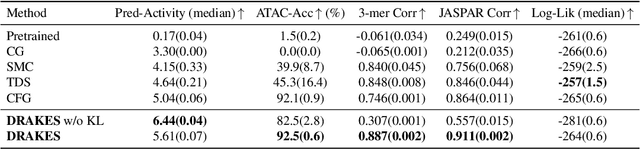
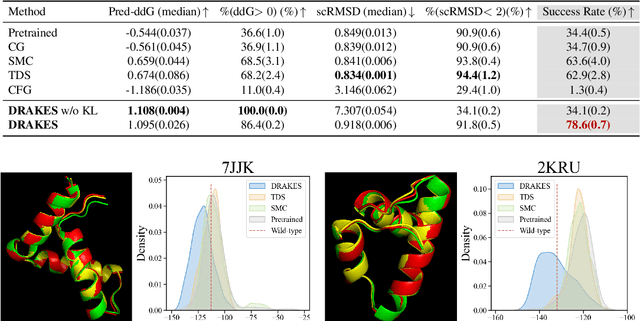

Abstract:Recent studies have demonstrated the strong empirical performance of diffusion models on discrete sequences across domains from natural language to biological sequence generation. For example, in the protein inverse folding task, conditional diffusion models have achieved impressive results in generating natural-like sequences that fold back into the original structure. However, practical design tasks often require not only modeling a conditional distribution but also optimizing specific task objectives. For instance, we may prefer protein sequences with high stability. To address this, we consider the scenario where we have pre-trained discrete diffusion models that can generate natural-like sequences, as well as reward models that map sequences to task objectives. We then formulate the reward maximization problem within discrete diffusion models, analogous to reinforcement learning (RL), while minimizing the KL divergence against pretrained diffusion models to preserve naturalness. To solve this RL problem, we propose a novel algorithm, DRAKES, that enables direct backpropagation of rewards through entire trajectories generated by diffusion models, by making the originally non-differentiable trajectories differentiable using the Gumbel-Softmax trick. Our theoretical analysis indicates that our approach can generate sequences that are both natural-like and yield high rewards. While similar tasks have been recently explored in diffusion models for continuous domains, our work addresses unique algorithmic and theoretical challenges specific to discrete diffusion models, which arise from their foundation in continuous-time Markov chains rather than Brownian motion. Finally, we demonstrate the effectiveness of DRAKES in generating DNA and protein sequences that optimize enhancer activity and protein stability, respectively, important tasks for gene therapies and protein-based therapeutics.
How to Build the Virtual Cell with Artificial Intelligence: Priorities and Opportunities
Sep 18, 2024

Abstract:The cell is arguably the smallest unit of life and is central to understanding biology. Accurate modeling of cells is important for this understanding as well as for determining the root causes of disease. Recent advances in artificial intelligence (AI), combined with the ability to generate large-scale experimental data, present novel opportunities to model cells. Here we propose a vision of AI-powered Virtual Cells, where robust representations of cells and cellular systems under different conditions are directly learned from growing biological data across measurements and scales. We discuss desired capabilities of AI Virtual Cells, including generating universal representations of biological entities across scales, and facilitating interpretable in silico experiments to predict and understand their behavior using Virtual Instruments. We further address the challenges, opportunities and requirements to realize this vision including data needs, evaluation strategies, and community standards and engagement to ensure biological accuracy and broad utility. We envision a future where AI Virtual Cells help identify new drug targets, predict cellular responses to perturbations, as well as scale hypothesis exploration. With open science collaborations across the biomedical ecosystem that includes academia, philanthropy, and the biopharma and AI industries, a comprehensive predictive understanding of cell mechanisms and interactions is within reach.
Derivative-Free Guidance in Continuous and Discrete Diffusion Models with Soft Value-Based Decoding
Aug 15, 2024



Abstract:Diffusion models excel at capturing the natural design spaces of images, molecules, DNA, RNA, and protein sequences. However, rather than merely generating designs that are natural, we often aim to optimize downstream reward functions while preserving the naturalness of these design spaces. Existing methods for achieving this goal often require ``differentiable'' proxy models (\textit{e.g.}, classifier guidance or DPS) or involve computationally expensive fine-tuning of diffusion models (\textit{e.g.}, classifier-free guidance, RL-based fine-tuning). In our work, we propose a new method to address these challenges. Our algorithm is an iterative sampling method that integrates soft value functions, which looks ahead to how intermediate noisy states lead to high rewards in the future, into the standard inference procedure of pre-trained diffusion models. Notably, our approach avoids fine-tuning generative models and eliminates the need to construct differentiable models. This enables us to (1) directly utilize non-differentiable features/reward feedback, commonly used in many scientific domains, and (2) apply our method to recent discrete diffusion models in a principled way. Finally, we demonstrate the effectiveness of our algorithm across several domains, including image generation, molecule generation, and DNA/RNA sequence generation. The code is available at \href{https://github.com/masa-ue/SVDD}{https://github.com/masa-ue/SVDD}.
Toward the Identifiability of Comparative Deep Generative Models
Jan 29, 2024



Abstract:Deep Generative Models (DGMs) are versatile tools for learning data representations while adequately incorporating domain knowledge such as the specification of conditional probability distributions. Recently proposed DGMs tackle the important task of comparing data sets from different sources. One such example is the setting of contrastive analysis that focuses on describing patterns that are enriched in a target data set compared to a background data set. The practical deployment of those models often assumes that DGMs naturally infer interpretable and modular latent representations, which is known to be an issue in practice. Consequently, existing methods often rely on ad-hoc regularization schemes, although without any theoretical grounding. Here, we propose a theory of identifiability for comparative DGMs by extending recent advances in the field of non-linear independent component analysis. We show that, while these models lack identifiability across a general class of mixing functions, they surprisingly become identifiable when the mixing function is piece-wise affine (e.g., parameterized by a ReLU neural network). We also investigate the impact of model misspecification, and empirically show that previously proposed regularization techniques for fitting comparative DGMs help with identifiability when the number of latent variables is not known in advance. Finally, we introduce a novel methodology for fitting comparative DGMs that improves the treatment of multiple data sources via multi-objective optimization and that helps adjust the hyperparameter for the regularization in an interpretable manner, using constrained optimization. We empirically validate our theory and new methodology using simulated data as well as a recent data set of genetic perturbations in cells profiled via single-cell RNA sequencing.
* 45 pages, 3 figures
Learning Causal Representations of Single Cells via Sparse Mechanism Shift Modeling
Nov 09, 2022



Abstract:Latent variable models such as the Variational Auto-Encoder (VAE) have become a go-to tool for analyzing biological data, especially in the field of single-cell genomics. One remaining challenge is the interpretability of latent variables as biological processes that define a cell's identity. Outside of biological applications, this problem is commonly referred to as learning disentangled representations. Although several disentanglement-promoting variants of the VAE were introduced, and applied to single-cell genomics data, this task has been shown to be infeasible from independent and identically distributed measurements, without additional structure. Instead, recent methods propose to leverage non-stationary data, as well as the sparse mechanism shift assumption in order to learn disentangled representations with a causal semantic. Here, we extend the application of these methodological advances to the analysis of single-cell genomics data with genetic or chemical perturbations. More precisely, we propose a deep generative model of single-cell gene expression data for which each perturbation is treated as a stochastic intervention targeting an unknown, but sparse, subset of latent variables. We benchmark these methods on simulated single-cell data to evaluate their performance at latent units recovery, causal target identification and out-of-domain generalization. Finally, we apply those approaches to two real-world large-scale gene perturbation data sets and find that models that exploit the sparse mechanism shift hypothesis surpass contemporary methods on a transfer learning task. We implement our new model and benchmarks using the scvi-tools library, and release it as open-source software at https://github.com/Genentech/sVAE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge