Yulai Zhao
Reward-Guided Iterative Refinement in Diffusion Models at Test-Time with Applications to Protein and DNA Design
Feb 20, 2025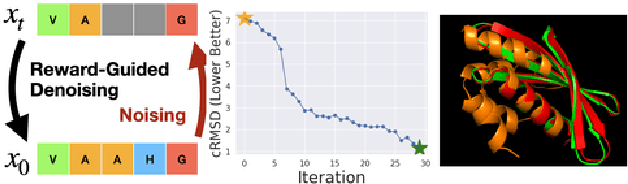
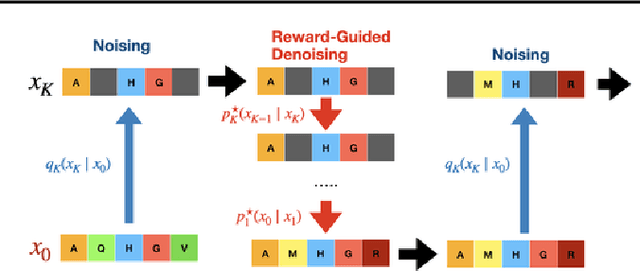
Abstract:To fully leverage the capabilities of diffusion models, we are often interested in optimizing downstream reward functions during inference. While numerous algorithms for reward-guided generation have been recently proposed due to their significance, current approaches predominantly focus on single-shot generation, transitioning from fully noised to denoised states. We propose a novel framework for inference-time reward optimization with diffusion models inspired by evolutionary algorithms. Our approach employs an iterative refinement process consisting of two steps in each iteration: noising and reward-guided denoising. This sequential refinement allows for the gradual correction of errors introduced during reward optimization. Besides, we provide a theoretical guarantee for our framework. Finally, we demonstrate its superior empirical performance in protein and cell-type-specific regulatory DNA design. The code is available at \href{https://github.com/masa-ue/ProDifEvo-Refinement}{https://github.com/masa-ue/ProDifEvo-Refinement}.
Reward-Guided Controlled Generation for Inference-Time Alignment in Diffusion Models: Tutorial and Review
Jan 16, 2025



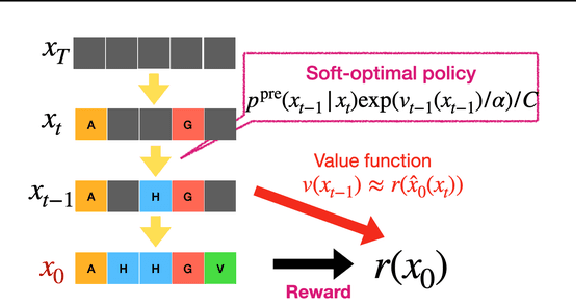
Abstract:This tutorial provides an in-depth guide on inference-time guidance and alignment methods for optimizing downstream reward functions in diffusion models. While diffusion models are renowned for their generative modeling capabilities, practical applications in fields such as biology often require sample generation that maximizes specific metrics (e.g., stability, affinity in proteins, closeness to target structures). In these scenarios, diffusion models can be adapted not only to generate realistic samples but also to explicitly maximize desired measures at inference time without fine-tuning. This tutorial explores the foundational aspects of such inference-time algorithms. We review these methods from a unified perspective, demonstrating that current techniques -- such as Sequential Monte Carlo (SMC)-based guidance, value-based sampling, and classifier guidance -- aim to approximate soft optimal denoising processes (a.k.a. policies in RL) that combine pre-trained denoising processes with value functions serving as look-ahead functions that predict from intermediate states to terminal rewards. Within this framework, we present several novel algorithms not yet covered in the literature. Furthermore, we discuss (1) fine-tuning methods combined with inference-time techniques, (2) inference-time algorithms based on search algorithms such as Monte Carlo tree search, which have received limited attention in current research, and (3) connections between inference-time algorithms in language models and diffusion models. The code of this tutorial on protein design is available at https://github.com/masa-ue/AlignInversePro
Derivative-Free Guidance in Continuous and Discrete Diffusion Models with Soft Value-Based Decoding
Aug 15, 2024



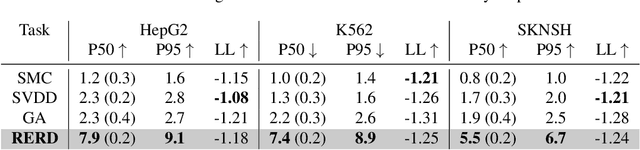
Abstract:Diffusion models excel at capturing the natural design spaces of images, molecules, DNA, RNA, and protein sequences. However, rather than merely generating designs that are natural, we often aim to optimize downstream reward functions while preserving the naturalness of these design spaces. Existing methods for achieving this goal often require ``differentiable'' proxy models (\textit{e.g.}, classifier guidance or DPS) or involve computationally expensive fine-tuning of diffusion models (\textit{e.g.}, classifier-free guidance, RL-based fine-tuning). In our work, we propose a new method to address these challenges. Our algorithm is an iterative sampling method that integrates soft value functions, which looks ahead to how intermediate noisy states lead to high rewards in the future, into the standard inference procedure of pre-trained diffusion models. Notably, our approach avoids fine-tuning generative models and eliminates the need to construct differentiable models. This enables us to (1) directly utilize non-differentiable features/reward feedback, commonly used in many scientific domains, and (2) apply our method to recent discrete diffusion models in a principled way. Finally, we demonstrate the effectiveness of our algorithm across several domains, including image generation, molecule generation, and DNA/RNA sequence generation. The code is available at \href{https://github.com/masa-ue/SVDD}{https://github.com/masa-ue/SVDD}.
Understanding Reinforcement Learning-Based Fine-Tuning of Diffusion Models: A Tutorial and Review
Jul 18, 2024



Abstract:This tutorial provides a comprehensive survey of methods for fine-tuning diffusion models to optimize downstream reward functions. While diffusion models are widely known to provide excellent generative modeling capability, practical applications in domains such as biology require generating samples that maximize some desired metric (e.g., translation efficiency in RNA, docking score in molecules, stability in protein). In these cases, the diffusion model can be optimized not only to generate realistic samples but also to explicitly maximize the measure of interest. Such methods are based on concepts from reinforcement learning (RL). We explain the application of various RL algorithms, including PPO, differentiable optimization, reward-weighted MLE, value-weighted sampling, and path consistency learning, tailored specifically for fine-tuning diffusion models. We aim to explore fundamental aspects such as the strengths and limitations of different RL-based fine-tuning algorithms across various scenarios, the benefits of RL-based fine-tuning compared to non-RL-based approaches, and the formal objectives of RL-based fine-tuning (target distributions). Additionally, we aim to examine their connections with related topics such as classifier guidance, Gflownets, flow-based diffusion models, path integral control theory, and sampling from unnormalized distributions such as MCMC. The code of this tutorial is available at https://github.com/masa-ue/RLfinetuning_Diffusion_Bioseq
Adding Conditional Control to Diffusion Models with Reinforcement Learning
Jun 17, 2024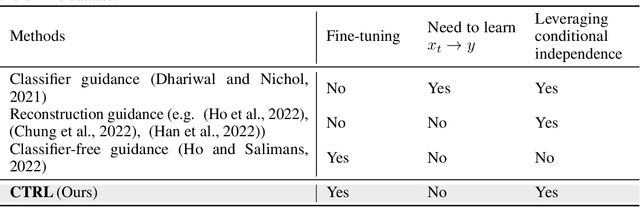
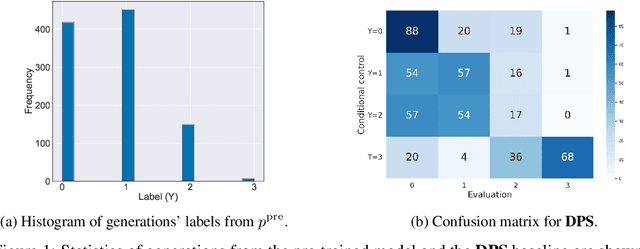
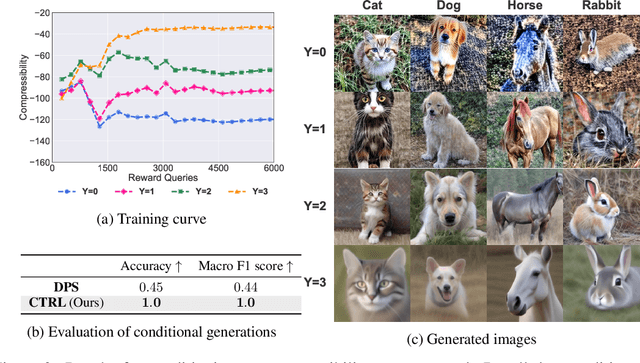
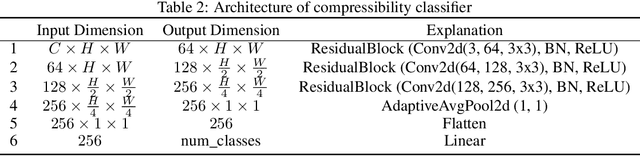
Abstract:Diffusion models are powerful generative models that allow for precise control over the characteristics of the generated samples. While these diffusion models trained on large datasets have achieved success, there is often a need to introduce additional controls in downstream fine-tuning processes, treating these powerful models as pre-trained diffusion models. This work presents a novel method based on reinforcement learning (RL) to add additional controls, leveraging an offline dataset comprising inputs and corresponding labels. We formulate this task as an RL problem, with the classifier learned from the offline dataset and the KL divergence against pre-trained models serving as the reward functions. We introduce our method, $\textbf{CTRL}$ ($\textbf{C}$onditioning pre-$\textbf{T}$rained diffusion models with $\textbf{R}$einforcement $\textbf{L}$earning), which produces soft-optimal policies that maximize the abovementioned reward functions. We formally demonstrate that our method enables sampling from the conditional distribution conditioned on additional controls during inference. Our RL-based approach offers several advantages over existing methods. Compared to commonly used classifier-free guidance, our approach improves sample efficiency, and can greatly simplify offline dataset construction by exploiting conditional independence between the inputs and additional controls. Furthermore, unlike classifier guidance, we avoid the need to train classifiers from intermediate states to additional controls.
Bridging Model-Based Optimization and Generative Modeling via Conservative Fine-Tuning of Diffusion Models
May 31, 2024



Abstract:AI-driven design problems, such as DNA/protein sequence design, are commonly tackled from two angles: generative modeling, which efficiently captures the feasible design space (e.g., natural images or biological sequences), and model-based optimization, which utilizes reward models for extrapolation. To combine the strengths of both approaches, we adopt a hybrid method that fine-tunes cutting-edge diffusion models by optimizing reward models through RL. Although prior work has explored similar avenues, they primarily focus on scenarios where accurate reward models are accessible. In contrast, we concentrate on an offline setting where a reward model is unknown, and we must learn from static offline datasets, a common scenario in scientific domains. In offline scenarios, existing approaches tend to suffer from overoptimization, as they may be misled by the reward model in out-of-distribution regions. To address this, we introduce a conservative fine-tuning approach, BRAID, by optimizing a conservative reward model, which includes additional penalization outside of offline data distributions. Through empirical and theoretical analysis, we demonstrate the capability of our approach to outperform the best designs in offline data, leveraging the extrapolation capabilities of reward models while avoiding the generation of invalid designs through pre-trained diffusion models.
Fine-Tuning of Continuous-Time Diffusion Models as Entropy-Regularized Control
Feb 28, 2024



Abstract:Diffusion models excel at capturing complex data distributions, such as those of natural images and proteins. While diffusion models are trained to represent the distribution in the training dataset, we often are more concerned with other properties, such as the aesthetic quality of the generated images or the functional properties of generated proteins. Diffusion models can be finetuned in a goal-directed way by maximizing the value of some reward function (e.g., the aesthetic quality of an image). However, these approaches may lead to reduced sample diversity, significant deviations from the training data distribution, and even poor sample quality due to the exploitation of an imperfect reward function. The last issue often occurs when the reward function is a learned model meant to approximate a ground-truth "genuine" reward, as is the case in many practical applications. These challenges, collectively termed "reward collapse," pose a substantial obstacle. To address this reward collapse, we frame the finetuning problem as entropy-regularized control against the pretrained diffusion model, i.e., directly optimizing entropy-enhanced rewards with neural SDEs. We present theoretical and empirical evidence that demonstrates our framework is capable of efficiently generating diverse samples with high genuine rewards, mitigating the overoptimization of imperfect reward models.
Feedback Efficient Online Fine-Tuning of Diffusion Models
Feb 27, 2024



Abstract:Diffusion models excel at modeling complex data distributions, including those of images, proteins, and small molecules. However, in many cases, our goal is to model parts of the distribution that maximize certain properties: for example, we may want to generate images with high aesthetic quality, or molecules with high bioactivity. It is natural to frame this as a reinforcement learning (RL) problem, in which the objective is to fine-tune a diffusion model to maximize a reward function that corresponds to some property. Even with access to online queries of the ground-truth reward function, efficiently discovering high-reward samples can be challenging: they might have a low probability in the initial distribution, and there might be many infeasible samples that do not even have a well-defined reward (e.g., unnatural images or physically impossible molecules). In this work, we propose a novel reinforcement learning procedure that efficiently explores on the manifold of feasible samples. We present a theoretical analysis providing a regret guarantee, as well as empirical validation across three domains: images, biological sequences, and molecules.
Provably Efficient CVaR RL in Low-rank MDPs
Nov 20, 2023Abstract:We study risk-sensitive Reinforcement Learning (RL), where we aim to maximize the Conditional Value at Risk (CVaR) with a fixed risk tolerance $\tau$. Prior theoretical work studying risk-sensitive RL focuses on the tabular Markov Decision Processes (MDPs) setting. To extend CVaR RL to settings where state space is large, function approximation must be deployed. We study CVaR RL in low-rank MDPs with nonlinear function approximation. Low-rank MDPs assume the underlying transition kernel admits a low-rank decomposition, but unlike prior linear models, low-rank MDPs do not assume the feature or state-action representation is known. We propose a novel Upper Confidence Bound (UCB) bonus-driven algorithm to carefully balance the interplay between exploration, exploitation, and representation learning in CVaR RL. We prove that our algorithm achieves a sample complexity of $\tilde{O}\left(\frac{H^7 A^2 d^4}{\tau^2 \epsilon^2}\right)$ to yield an $\epsilon$-optimal CVaR, where $H$ is the length of each episode, $A$ is the capacity of action space, and $d$ is the dimension of representations. Computational-wise, we design a novel discretized Least-Squares Value Iteration (LSVI) algorithm for the CVaR objective as the planning oracle and show that we can find the near-optimal policy in a polynomial running time with a Maximum Likelihood Estimation oracle. To our knowledge, this is the first provably efficient CVaR RL algorithm in low-rank MDPs.
Local Optimization Achieves Global Optimality in Multi-Agent Reinforcement Learning
May 08, 2023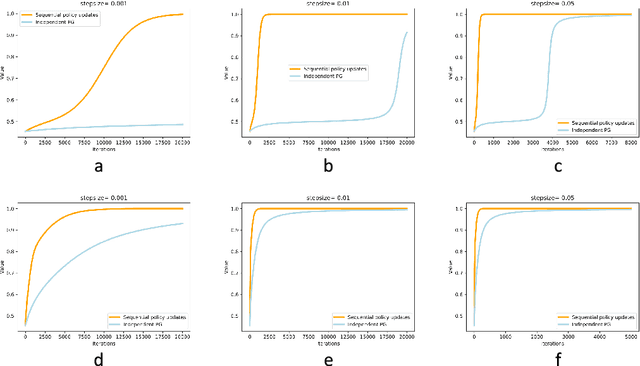
Abstract:Policy optimization methods with function approximation are widely used in multi-agent reinforcement learning. However, it remains elusive how to design such algorithms with statistical guarantees. Leveraging a multi-agent performance difference lemma that characterizes the landscape of multi-agent policy optimization, we find that the localized action value function serves as an ideal descent direction for each local policy. Motivated by the observation, we present a multi-agent PPO algorithm in which the local policy of each agent is updated similarly to vanilla PPO. We prove that with standard regularity conditions on the Markov game and problem-dependent quantities, our algorithm converges to the globally optimal policy at a sublinear rate. We extend our algorithm to the off-policy setting and introduce pessimism to policy evaluation, which aligns with experiments. To our knowledge, this is the first provably convergent multi-agent PPO algorithm in cooperative Markov games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge