Diamond Maps: Efficient Reward Alignment via Stochastic Flow Maps

Flow and diffusion models produce high-quality samples, but adapting them to user preferences or constraints post-training remains costly and brittle, a challenge commonly called reward alignment. We argue that efficient reward alignment should be a property of the generative model itself, not an afterthought, and redesign the model for adaptability. We propose "Diamond Maps", stochastic flow map models that enable efficient and accurate alignment to arbitrary rewards at inference time. Diamond Maps amortize many simulation steps into a single-step sampler, like flow maps, while preserving the stochasticity required for optimal reward alignment. This design makes search, sequential Monte Carlo, and guidance scalable by enabling efficient and consistent estimation of the value function. Our experiments show that Diamond Maps can be learned efficiently via distillation from GLASS Flows, achieve stronger reward alignment performance, and scale better than existing methods. Our results point toward a practical route to generative models that can be rapidly adapted to arbitrary preferences and constraints at inference time.

FragmentFlow: Scalable Transition State Generation for Large Molecules

Transition states (TSs) are central to understanding and quantitatively predicting chemical reactivity and reaction mechanisms. Although traditional TS generation methods are computationally expensive, recent generative modeling approaches have enabled chemically meaningful TS prediction for relatively small molecules. However, these methods fail to generalize to practically relevant reaction substrates because of distribution shifts induced by increasing molecular sizes. Furthermore, TS geometries for larger molecules are not available at scale, making it infeasible to train generative models from scratch on such molecules. To address these challenges, we introduce FragmentFlow: a divide-and-conquer approach that trains a generative model to predict TS geometries for the reactive core atoms, which define the reaction mechanism. The full TS structure is then reconstructed by re-attaching substituent fragments to the predicted core. By operating on reactive cores, whose size and composition remain relatively invariant across molecular contexts, FragmentFlow mitigates distribution shifts in generative modeling. Evaluated on a new curated dataset of reactions involving reactants with up to 33 heavy atoms, FragmentFlow correctly identifies 90% of TSs while requiring 30% fewer saddle-point optimization steps than classical initialization schemes. These results point toward scalable TS generation for high-throughput reactivity studies.

SPG: Sandwiched Policy Gradient for Masked Diffusion Language Models

Diffusion large language models (dLLMs) are emerging as an efficient alternative to autoregressive models due to their ability to decode multiple tokens in parallel. However, aligning dLLMs with human preferences or task-specific rewards via reinforcement learning (RL) is challenging because their intractable log-likelihood precludes the direct application of standard policy gradient methods. While prior work uses surrogates like the evidence lower bound (ELBO), these one-sided approximations can introduce significant policy gradient bias. To address this, we propose the Sandwiched Policy Gradient (SPG) that leverages both an upper and a lower bound of the true log-likelihood. Experiments show that SPG significantly outperforms baselines based on ELBO or one-step estimation. Specifically, SPG improves the accuracy over state-of-the-art RL methods for dLLMs by 3.6% in GSM8K, 2.6% in MATH500, 18.4% in Countdown and 27.0% in Sudoku.

ProxelGen: Generating Proteins as 3D Densities

We develop ProxelGen, a protein structure generative model that operates on 3D densities as opposed to the prevailing 3D point cloud representations. Representing proteins as voxelized densities, or proxels, enables new tasks and conditioning capabilities. We generate proteins encoded as proxels via a 3D CNN-based VAE in conjunction with a diffusion model operating on its latent space. Compared to state-of-the-art models, ProxelGen's samples achieve higher novelty, better FID scores, and the same level of designability as the training set. ProxelGen's advantages are demonstrated in a standard motif scaffolding benchmark, and we show how 3D density-based generation allows for more flexible shape conditioning.

Thought calibration: Efficient and confident test-time scaling

Reasoning large language models achieve impressive test-time scaling by thinking for longer, but this performance gain comes at significant compute cost. Directly limiting test-time budget hurts overall performance, but not all problems are equally difficult. We propose thought calibration to decide dynamically when thinking can be terminated. To calibrate our decision rule, we view a language model's growing body of thoughts as a nested sequence of reasoning trees, where the goal is to identify the point at which novel reasoning plateaus. We realize this framework through lightweight probes that operate on top of the language model's hidden representations, which are informative of both the reasoning structure and overall consistency of response. Based on three reasoning language models and four datasets, thought calibration preserves model performance with up to a 60% reduction in thinking tokens on in-distribution data, and up to 20% in out-of-distribution data.

Inference-Time Scaling for Diffusion Models beyond Scaling Denoising Steps

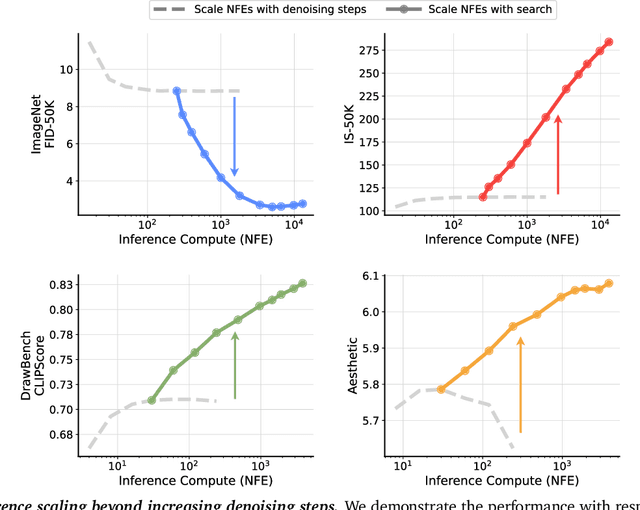
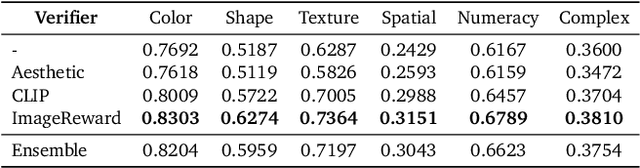
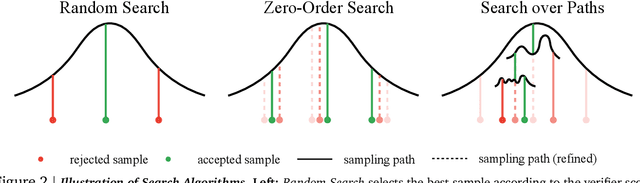
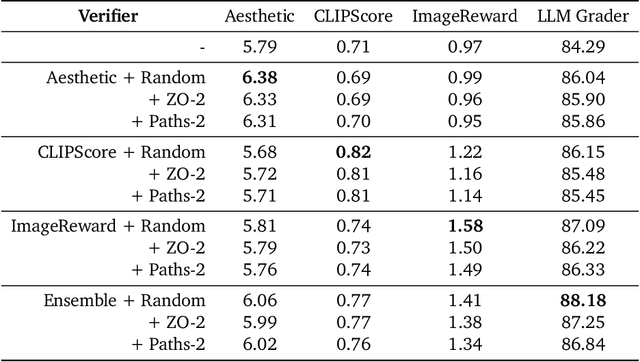
Generative models have made significant impacts across various domains, largely due to their ability to scale during training by increasing data, computational resources, and model size, a phenomenon characterized by the scaling laws. Recent research has begun to explore inference-time scaling behavior in Large Language Models (LLMs), revealing how performance can further improve with additional computation during inference. Unlike LLMs, diffusion models inherently possess the flexibility to adjust inference-time computation via the number of denoising steps, although the performance gains typically flatten after a few dozen. In this work, we explore the inference-time scaling behavior of diffusion models beyond increasing denoising steps and investigate how the generation performance can further improve with increased computation. Specifically, we consider a search problem aimed at identifying better noises for the diffusion sampling process. We structure the design space along two axes: the verifiers used to provide feedback, and the algorithms used to find better noise candidates. Through extensive experiments on class-conditioned and text-conditioned image generation benchmarks, our findings reveal that increasing inference-time compute leads to substantial improvements in the quality of samples generated by diffusion models, and with the complicated nature of images, combinations of the components in the framework can be specifically chosen to conform with different application scenario.

An Information Criterion for Controlled Disentanglement of Multimodal Data

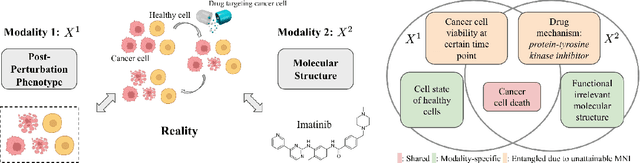
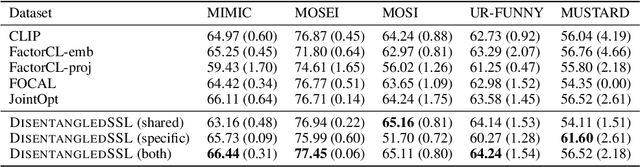
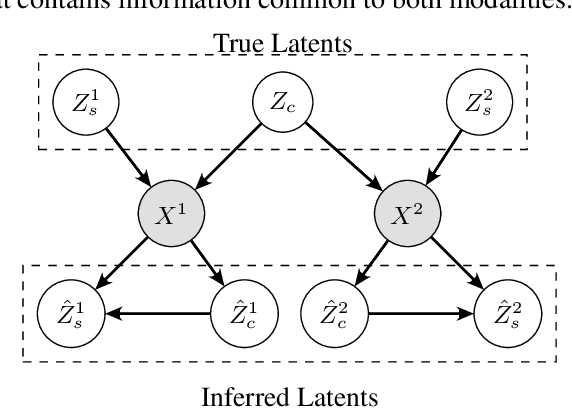
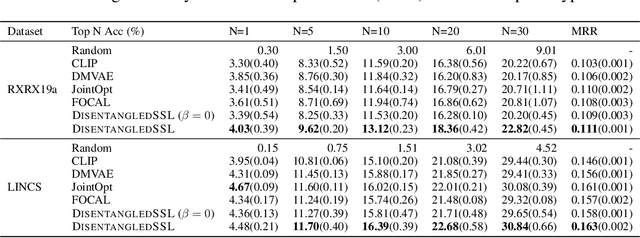
Multimodal representation learning seeks to relate and decompose information inherent in multiple modalities. By disentangling modality-specific information from information that is shared across modalities, we can improve interpretability and robustness and enable downstream tasks such as the generation of counterfactual outcomes. Separating the two types of information is challenging since they are often deeply entangled in many real-world applications. We propose Disentangled Self-Supervised Learning (DisentangledSSL), a novel self-supervised approach for learning disentangled representations. We present a comprehensive analysis of the optimality of each disentangled representation, particularly focusing on the scenario not covered in prior work where the so-called Minimum Necessary Information (MNI) point is not attainable. We demonstrate that DisentangledSSL successfully learns shared and modality-specific features on multiple synthetic and real-world datasets and consistently outperforms baselines on various downstream tasks, including prediction tasks for vision-language data, as well as molecule-phenotype retrieval tasks for biological data.

Generator Matching: Generative modeling with arbitrary Markov processes

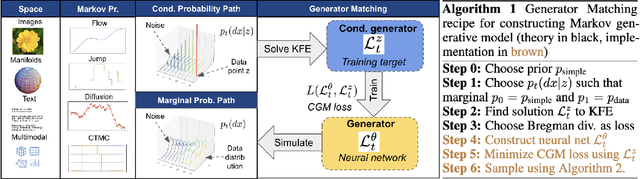
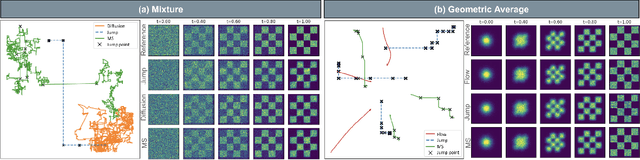
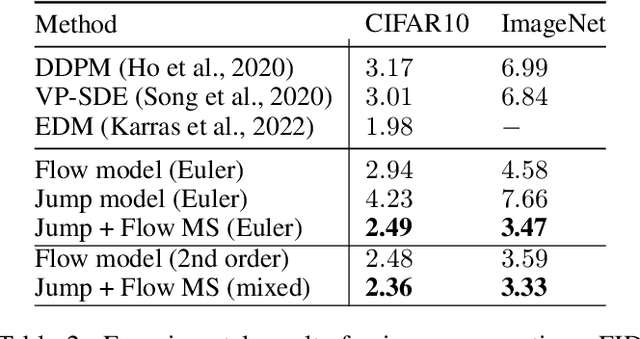
We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.

A Cosmic-Scale Benchmark for Symmetry-Preserving Data Processing

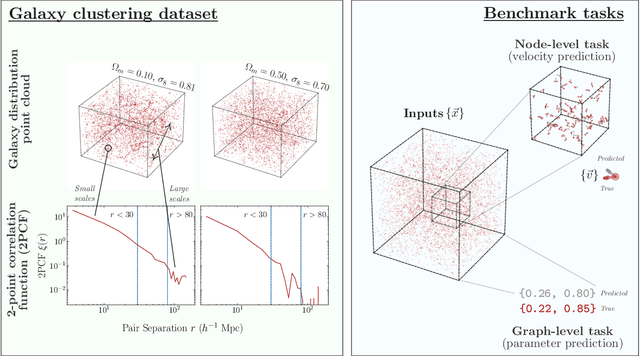
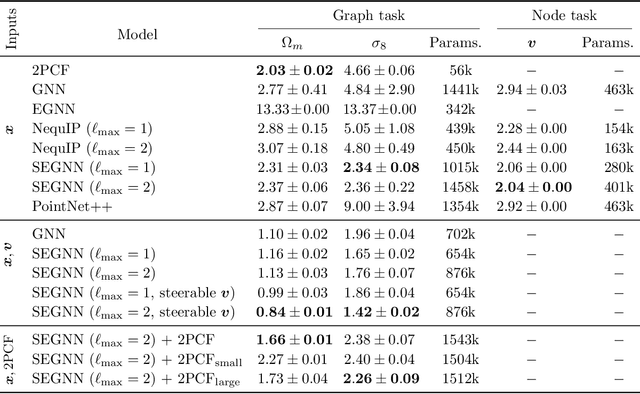
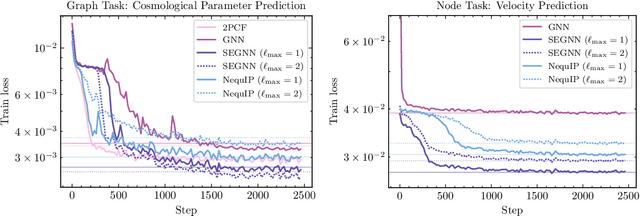
Efficiently processing structured point cloud data while preserving multiscale information is a key challenge across domains, from graphics to atomistic modeling. Using a curated dataset of simulated galaxy positions and properties, represented as point clouds, we benchmark the ability of graph neural networks to simultaneously capture local clustering environments and long-range correlations. Given the homogeneous and isotropic nature of the Universe, the data exhibits a high degree of symmetry. We therefore focus on evaluating the performance of Euclidean symmetry-preserving ($E(3)$-equivariant) graph neural networks, showing that they can outperform non-equivariant counterparts and domain-specific information extraction techniques in downstream performance as well as simulation-efficiency. However, we find that current architectures fail to capture information from long-range correlations as effectively as domain-specific baselines, motivating future work on architectures better suited for extracting long-range information.

Hamiltonian Score Matching and Generative Flows

Classical Hamiltonian mechanics has been widely used in machine learning in the form of Hamiltonian Monte Carlo for applications with predetermined force fields. In this work, we explore the potential of deliberately designing force fields for Hamiltonian ODEs, introducing Hamiltonian velocity predictors (HVPs) as a tool for score matching and generative models. We present two innovations constructed with HVPs: Hamiltonian Score Matching (HSM), which estimates score functions by augmenting data via Hamiltonian trajectories, and Hamiltonian Generative Flows (HGFs), a novel generative model that encompasses diffusion models and flow matching as HGFs with zero force fields. We showcase the extended design space of force fields by introducing Oscillation HGFs, a generative model inspired by harmonic oscillators. Our experiments validate our theoretical insights about HSM as a novel score matching metric and demonstrate that HGFs rival leading generative modeling techniques.