Generator Matching: Generative modeling with arbitrary Markov processes
Paper and Code
Oct 27, 2024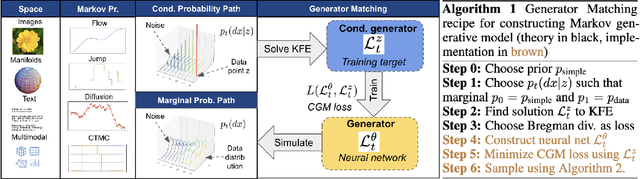

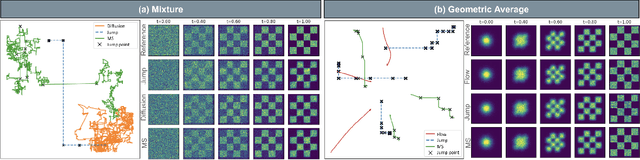
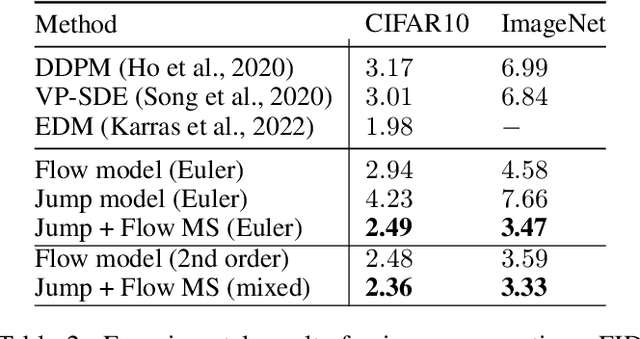
We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge