Discrete Flow Maps

The sequential nature of autoregressive next-token prediction imposes a fundamental speed limit on large language models. While continuous flow models offer a path to parallel generation, they traditionally demand expensive iterative integration. Flow Maps bypass this bottleneck by compressing generative trajectories into single-step mappings, theoretically enabling the generation of full text sequences from noise in a single forward pass. However, standard formulations rely on Euclidean regression losses that are geometrically ill-suited for discrete data. In this work, we resolve this conflict with Discrete Flow Maps, a framework that reconciles trajectory compression with the geometry of the probability simplex. We recast standard flow map training for the discrete domain, aligning the training dynamics with the discrete nature of language. Empirically, this strict geometric alignment allows our method to surpass previous state-of-the-art results in discrete flow modeling.

MotifBench: A standardized protein design benchmark for motif-scaffolding problems

The motif-scaffolding problem is a central task in computational protein design: Given the coordinates of atoms in a geometry chosen to confer a desired biochemical function (a motif), the task is to identify diverse protein structures (scaffolds) that include the motif and maintain its geometry. Significant recent progress on motif-scaffolding has been made due to computational evaluation with reliable protein structure prediction and fixed-backbone sequence design methods. However, significant variability in evaluation strategies across publications has hindered comparability of results, challenged reproducibility, and impeded robust progress. In response we introduce MotifBench, comprising (1) a precisely specified pipeline and evaluation metrics, (2) a collection of 30 benchmark problems, and (3) an implementation of this benchmark and leaderboard at github.com/blt2114/MotifBench. The MotifBench test cases are more difficult compared to earlier benchmarks, and include protein design problems for which solutions are known but on which, to the best of our knowledge, state-of-the-art methods fail to identify any solution.

Generator Matching: Generative modeling with arbitrary Markov processes

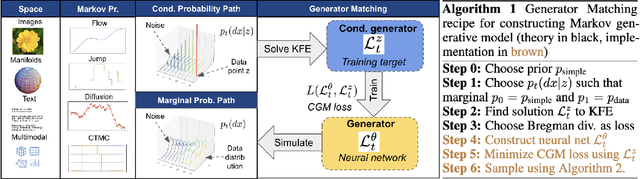
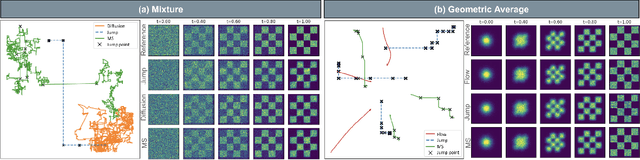
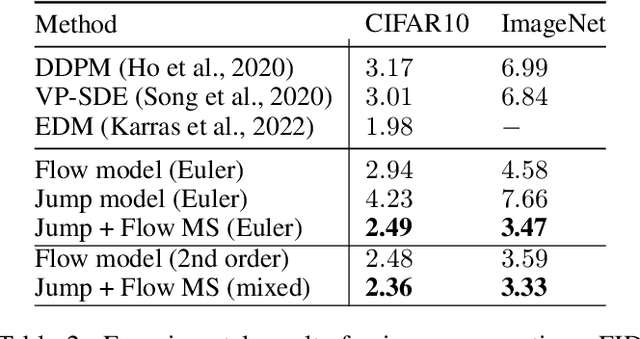
We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.

Generative Flows on Discrete State-Spaces: Enabling Multimodal Flows with Applications to Protein Co-Design

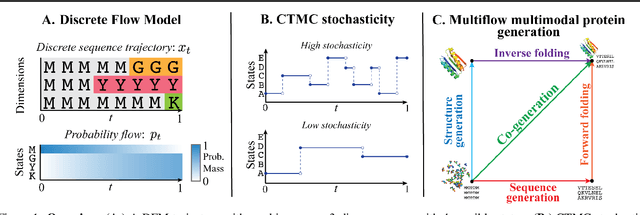
Combining discrete and continuous data is an important capability for generative models. We present Discrete Flow Models (DFMs), a new flow-based model of discrete data that provides the missing link in enabling flow-based generative models to be applied to multimodal continuous and discrete data problems. Our key insight is that the discrete equivalent of continuous space flow matching can be realized using Continuous Time Markov Chains. DFMs benefit from a simple derivation that includes discrete diffusion models as a specific instance while allowing improved performance over existing diffusion-based approaches. We utilize our DFMs method to build a multimodal flow-based modeling framework. We apply this capability to the task of protein co-design, wherein we learn a model for jointly generating protein structure and sequence. Our approach achieves state-of-the-art co-design performance while allowing the same multimodal model to be used for flexible generation of the sequence or structure.

Improved motif-scaffolding with SE(3) flow matching

Protein design often begins with knowledge of a desired function from a motif which motif-scaffolding aims to construct a functional protein around. Recently, generative models have achieved breakthrough success in designing scaffolds for a diverse range of motifs. However, the generated scaffolds tend to lack structural diversity, which can hinder success in wet-lab validation. In this work, we extend FrameFlow, an SE(3) flow matching model for protein backbone generation, to perform motif-scaffolding with two complementary approaches. The first is motif amortization, in which FrameFlow is trained with the motif as input using a data augmentation strategy. The second is motif guidance, which performs scaffolding using an estimate of the conditional score from FrameFlow, and requires no additional training. Both approaches achieve an equivalent or higher success rate than previous state-of-the-art methods, with 2.5 times more structurally diverse scaffolds. Code: https://github.com/ microsoft/frame-flow.

Fast non-autoregressive inverse folding with discrete diffusion

Generating protein sequences that fold into a intended 3D structure is a fundamental step in de novo protein design. De facto methods utilize autoregressive generation, but this eschews higher order interactions that could be exploited to improve inference speed. We describe a non-autoregressive alternative that performs inference using a constant number of calls resulting in a 23 times speed up without a loss in performance on the CATH benchmark. Conditioned on the 3D structure, we fine-tune ProteinMPNN to perform discrete diffusion with a purity prior over the index sampling order. Our approach gives the flexibility in trading off inference speed and accuracy by modulating the diffusion speed. Code: https://github.com/johnyang101/pmpnndiff

Optimizing protein fitness using Gibbs sampling with Graph-based Smoothing

The ability to design novel proteins with higher fitness on a given task would be revolutionary for many fields of medicine. However, brute-force search through the combinatorially large space of sequences is infeasible. Prior methods constrain search to a small mutational radius from a reference sequence, but such heuristics drastically limit the design space. Our work seeks to remove the restriction on mutational distance while enabling efficient exploration. We propose Gibbs sampling with Graph-based Smoothing (GGS) which iteratively applies Gibbs with gradients to propose advantageous mutations using graph-based smoothing to remove noisy gradients that lead to false positives. Our method is state-of-the-art in discovering high-fitness proteins with up to 8 mutations from the training set. We study the GFP and AAV design problems, ablations, and baselines to elucidate the results. Code: https://github.com/kirjner/GGS

SE(3) diffusion model with application to protein backbone generation

The design of novel protein structures remains a challenge in protein engineering for applications across biomedicine and chemistry. In this line of work, a diffusion model over rigid bodies in 3D (referred to as frames) has shown success in generating novel, functional protein backbones that have not been observed in nature. However, there exists no principled methodological framework for diffusion on SE(3), the space of orientation preserving rigid motions in R3, that operates on frames and confers the group invariance. We address these shortcomings by developing theoretical foundations of SE(3) invariant diffusion models on multiple frames followed by a novel framework, FrameDiff, for learning the SE(3) equivariant score over multiple frames. We apply FrameDiff on monomer backbone generation and find it can generate designable monomers up to 500 amino acids without relying on a pretrained protein structure prediction network that has been integral to previous methods. We find our samples are capable of generalizing beyond any known protein structure.

Diffusion probabilistic modeling of protein backbones in 3D for the motif-scaffolding problem

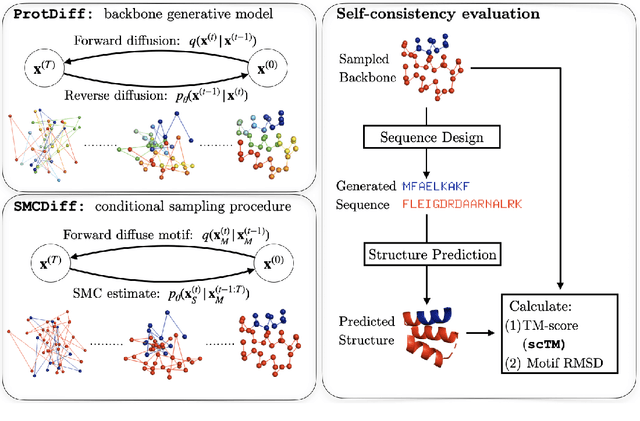
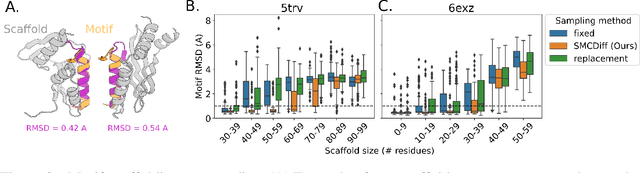
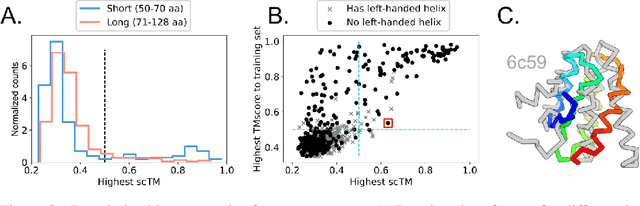
Construction of a scaffold structure that supports a desired motif, conferring protein function, shows promise for the design of vaccines and enzymes. But a general solution to this motif-scaffolding problem remains open. Current machine-learning techniques for scaffold design are either limited to unrealistically small scaffolds (up to length 20) or struggle to produce multiple diverse scaffolds. We propose to learn a distribution over diverse and longer protein backbone structures via an E(3)-equivariant graph neural network. We develop SMCDiff to efficiently sample scaffolds from this distribution conditioned on a given motif; our algorithm is the first to theoretically guarantee conditional samples from a diffusion model in the large-compute limit. We evaluate our designed backbones by how well they align with AlphaFold2-predicted structures. We show that our method can (1) sample scaffolds up to 80 residues and (2) achieve structurally diverse scaffolds for a fixed motif.

Random Projection Forests

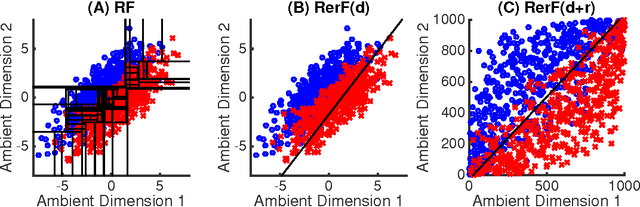
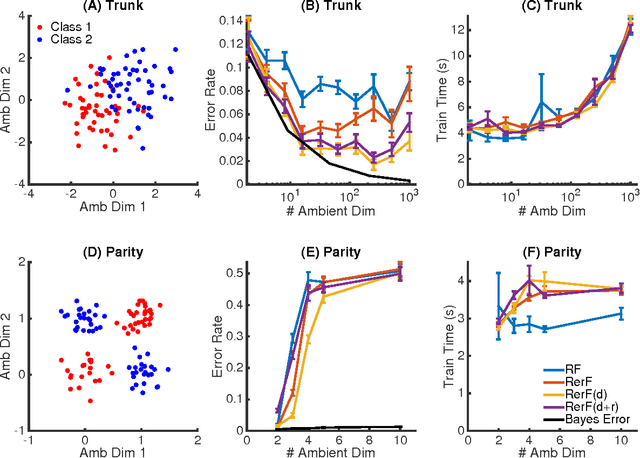
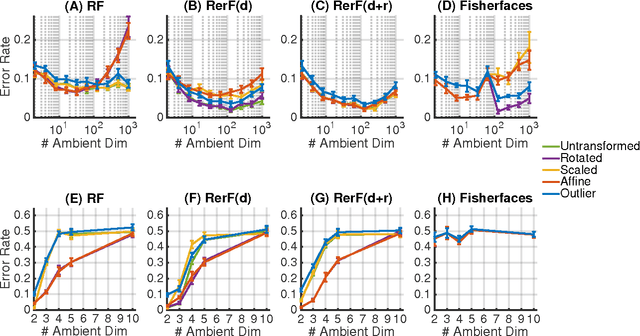
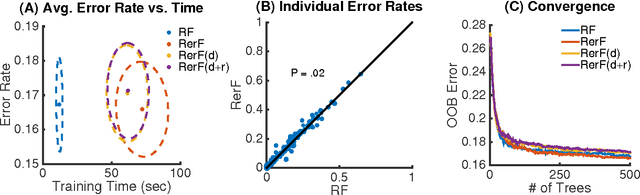
Ensemble methods---particularly those based on decision trees---have recently demonstrated superior performance in a variety of machine learning settings. We introduce a generalization of many existing decision tree methods called "Random Projection Forests" (RPF), which is any decision forest that uses (possibly data dependent and random) linear projections. Using this framework, we introduce a special case, called "Lumberjack", using very sparse random projections, that is, linear combinations of a small subset of features. Lumberjack obtains statistically significantly improved accuracy over Random Forests, Gradient Boosted Trees, and other approaches on a standard benchmark suites for classification with varying dimension, sample size, and number of classes. To illustrate how, why, and when Lumberjack outperforms other methods, we conduct extensive simulated experiments, in vectors, images, and nonlinear manifolds. Lumberjack typically yields improved performance over existing decision trees ensembles, while mitigating computational efficiency and scalability, and maintaining interpretability. Lumberjack can easily be incorporated into other ensemble methods such as boosting to obtain potentially similar gains.