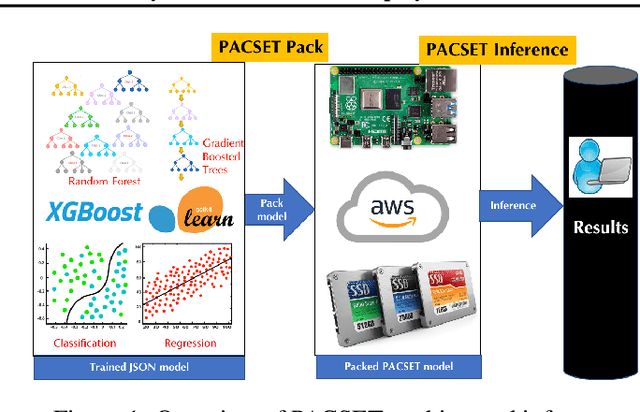
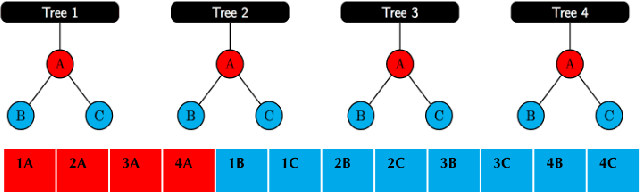
PACSET (Packed Serialized Trees): Reducing Inference Latency for Tree Ensemble Deployment

We present methods to serialize and deserialize tree ensembles that optimize inference latency when models are not already loaded into memory. This arises whenever models are larger than memory, but also systematically when models are deployed on low-resource devices, such as in the Internet of Things, or run as Web micro-services where resources are allocated on demand. Our packed serialized trees (PACSET) encode reference locality in the layout of a tree ensemble using principles from external memory algorithms. The layout interleaves correlated nodes across multiple trees, uses leaf cardinality to collocate the nodes on the most popular paths and is optimized for the I/O blocksize. The result is that each I/O yields a higher fraction of useful data, leading to a 2-6 times reduction in classification latency for interactive workloads.

Geodesic Learning via Unsupervised Decision Forests

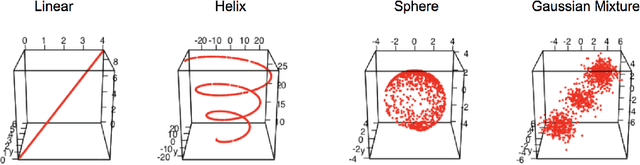
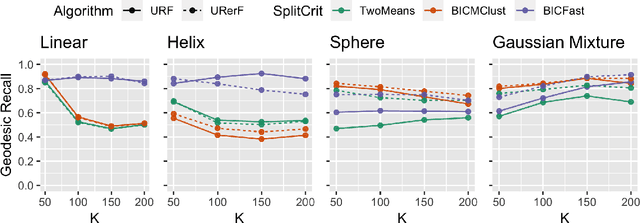
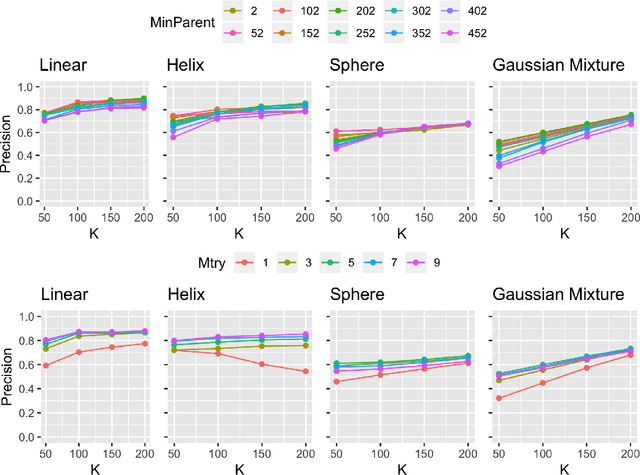
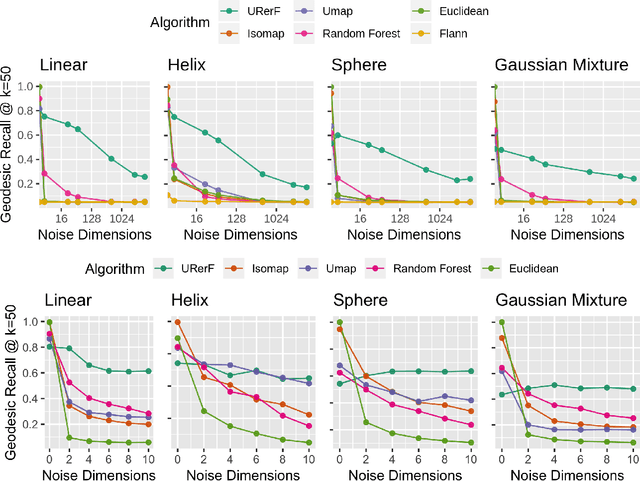
Geodesic distance is the shortest path between two points in a Riemannian manifold. Manifold learning algorithms, such as Isomap, seek to learn a manifold that preserves geodesic distances. However, such methods operate on the ambient dimensionality, and are therefore fragile to noise dimensions. We developed an unsupervised random forest method (URerF) to approximately learn geodesic distances in linear and nonlinear manifolds with noise. URerF operates on low-dimensional sparse linear combinations of features, rather than the full observed dimensionality. To choose the optimal split in a computationally efficient fashion, we developed a fast Bayesian Information Criterion statistic for Gaussian mixture models. We introduce geodesic precision-recall curves which quantify performance relative to the true latent manifold. Empirical results on simulated and real data demonstrate that URerF is robust to high-dimensional noise, where as other methods, such as Isomap, UMAP, and FLANN, quickly deteriorate in such settings. In particular, URerF is able to estimate geodesic distances on a real connectome dataset better than other approaches.

Random Projection Forests

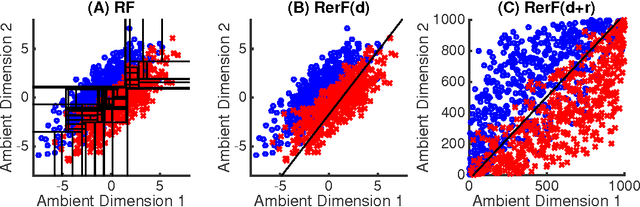
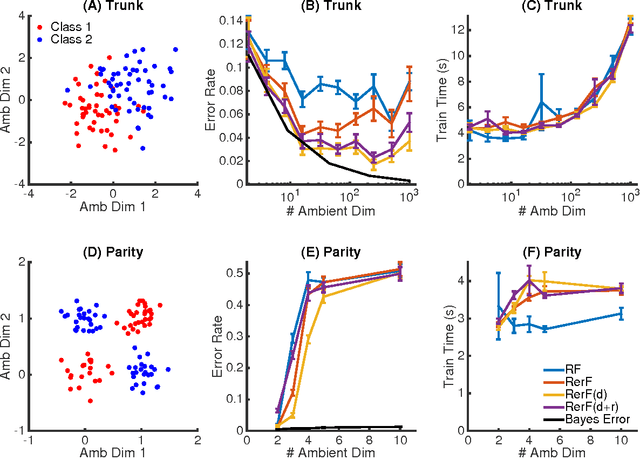
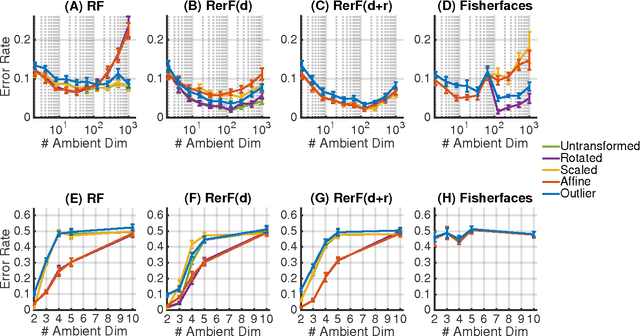
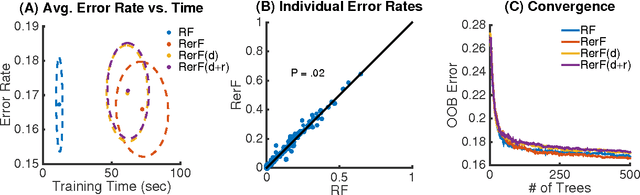
Ensemble methods---particularly those based on decision trees---have recently demonstrated superior performance in a variety of machine learning settings. We introduce a generalization of many existing decision tree methods called "Random Projection Forests" (RPF), which is any decision forest that uses (possibly data dependent and random) linear projections. Using this framework, we introduce a special case, called "Lumberjack", using very sparse random projections, that is, linear combinations of a small subset of features. Lumberjack obtains statistically significantly improved accuracy over Random Forests, Gradient Boosted Trees, and other approaches on a standard benchmark suites for classification with varying dimension, sample size, and number of classes. To illustrate how, why, and when Lumberjack outperforms other methods, we conduct extensive simulated experiments, in vectors, images, and nonlinear manifolds. Lumberjack typically yields improved performance over existing decision trees ensembles, while mitigating computational efficiency and scalability, and maintaining interpretability. Lumberjack can easily be incorporated into other ensemble methods such as boosting to obtain potentially similar gains.